Теорема о непринадлежности XOR классу AC⁰ — различия между версиями
Rost (обсуждение | вклад) |
Rost (обсуждение | вклад) |
||
| Строка 31: | Строка 31: | ||
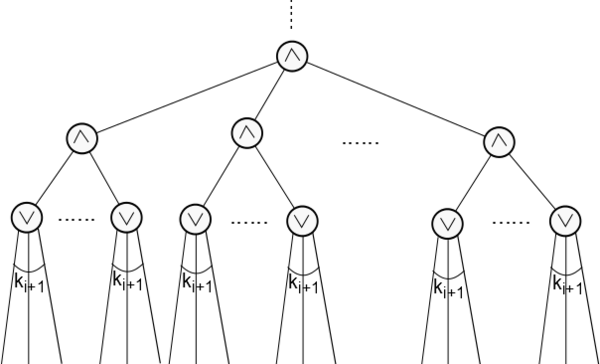
[[Файл:afterHastadSwitchingTransformation.png|600px|thumb|center|Схема на <tex>i+1</tex>-ом шаге.]] | [[Файл:afterHastadSwitchingTransformation.png|600px|thumb|center|Схема на <tex>i+1</tex>-ом шаге.]] | ||
| − | Заметим, что лемма применяется не более, чем к <tex>n^b</tex> элементам исходной схемы. Тогда с вероятностью <tex>9/10</tex> после <tex>d-2</tex>-ого шага получаем схему глубины <tex>2</tex>, у которой максимальная степень входа на нижнем уровне не больше <tex>k_{d-2}</tex>. По построению эта формула либо КНФ, либо ДНФ. Такую схему можно сделать постоянной, если правильно зафиксировать <tex>k_{d-2}</tex> переменных. Однако функцию <tex>\oplus</tex> невозможно сделать постоянной, зафиксировав менее <tex>n</tex> переменных. Получили противоречие. Поскольку рассматривали произвольную схему из класса <tex>\mathrm{AC^0}</tex>, верно что <tex>\oplus \notin \mathrm{AC^0}.</tex> | + | Заметим, что лемма применяется не более, чем к <tex>n^b</tex> элементам исходной схемы. Тогда с вероятностью не менее <tex>9/10</tex> после <tex>d-2</tex>-ого шага получаем схему глубины <tex>2</tex>, у которой максимальная степень входа на нижнем уровне не больше <tex>k_{d-2}</tex>. По построению эта формула либо КНФ, либо ДНФ. Такую схему можно сделать постоянной, если правильно зафиксировать <tex>k_{d-2}</tex> переменных. Однако функцию <tex>\oplus</tex> невозможно сделать постоянной, зафиксировав менее <tex>n</tex> переменных. Получили противоречие. Поскольку рассматривали произвольную схему из класса <tex>\mathrm{AC^0}</tex>, верно что <tex>\oplus \notin \mathrm{AC^0}.</tex> |
}} | }} | ||
| + | |||
| + | ===Источники=== | ||
| + | * ''Sanjeev Arora, Boaz Barak''. [http://www.cs.princeton.edu/theory/complexity Computational Complexity: A Modern Approach] | ||
Версия 23:33, 20 мая 2012
Hastad’s switching lemma
| Лемма: |
Заметим, что для функции можно получить такой же результат, изменив КНФ на ДНФ и наоборот.
Теорема
| Определение: |
| язык над алфавитом , состоящий из слов, содержащих нечетное число |
| Теорема: |
. |
| Доказательство: |
|
Рассмотрим произвольную схему из . Не умаляя общности, будем считать, что:
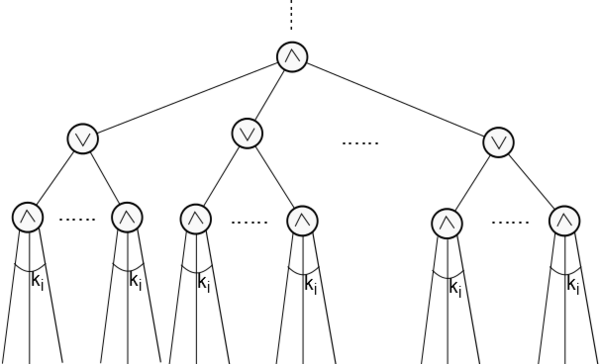
Построим итеративный процесс, на каждом шаге которого можно с высокой вероятностью на уменьшить глубину схемы, сохранив при этом число входов. Пусть длина входной цепочки, а глубина схемы. Выберем минимальное целое так, чтобы было не меньше, чем число элементов в схеме. На каждом шаге случайным образом будем назначать все большее число переменных. Обозначим число неназначенных переменных на -ом шаге. Тогда на -ом шаге число назначенных переменных будет . Возьмем Покажем, что после -ого шага глубина схемы будет , причем наибольшая степень входа элемента на нижнем уровне будет . В самом деле, пусть нижний уровень схемы состоит из элементов, тогда уровень выше из элементов . Каждый элемент можно считать -ДНФ. Отсюда по лемме получаем, что с вероятностью функцию можно записать в виде -КНФ. При достаточно больших это можно сделать с вероятность хотя бы . Поскольку верхний уровень КНФ состоит из элементов, также как и уровень над КНФ, то их можно объединить, уменьшив при этом глубину схемы на . Аналогично рассматриваем случай, когда нижний уровень схемы состоит из элементов. Заметим, что лемма применяется не более, чем к элементам исходной схемы. Тогда с вероятностью не менее после -ого шага получаем схему глубины , у которой максимальная степень входа на нижнем уровне не больше . По построению эта формула либо КНФ, либо ДНФ. Такую схему можно сделать постоянной, если правильно зафиксировать переменных. Однако функцию невозможно сделать постоянной, зафиксировав менее переменных. Получили противоречие. Поскольку рассматривали произвольную схему из класса , верно что |
Источники
- Sanjeev Arora, Boaz Barak. Computational Complexity: A Modern Approach