Задача многокритериальной оптимизации. Multiobjectivization — различия между версиями
(→Определение) |
(→Задача многокритериальной оптимизации) |
||
| Строка 16: | Строка 16: | ||
}} | }} | ||
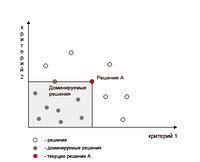
Выражение <math>x \succ x^*</math> означает, что <math>x</math> ''доминирует над'' <math>x^*</math>. | Выражение <math>x \succ x^*</math> означает, что <math>x</math> ''доминирует над'' <math>x^*</math>. | ||
| − | + | [[Файл:Dogmin points.jpg|мини|200px|Доминируемые решения]] | |
| − | |||
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | Для двух решений <math>x</math> и <math>x'</math> говорят <math>x \sim x'</math> тогда и только тогда, когда <math>\exists i \in 1..K \colon f_i(x) > f_i(x') \land \exists j \in 1..K, j \ne i \colon f_j(x') > f_j(x)</math> - такую пару решений называют ''' | + | Для двух решений <math>x</math> и <math>x'</math> говорят <math>x \sim x'</math> тогда и только тогда, когда <math>\exists i \in 1..K \colon f_i(x) > f_i(x') \land \exists j \in 1..K, j \ne i \colon f_j(x') > f_j(x)</math> - такую пару решений называют '''недоминируемой''' |
}} | }} | ||
| + | |||
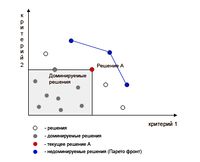
| + | Множество Парето оптимальных недоминируемых решений называется '''Парето фронтом.''' | ||
| + | [[Файл:Pareto_front.jpg|мини|200px|Парето фронт]] | ||
| + | == Получение оптимальных по Парето решений == | ||
| + | Для выполнения оптимизации по нескольким критериям мы должны либо заменить единственную целевую | ||
== Источники == | == Источники == | ||
Версия 03:57, 19 июня 2012
Содержание
Задача многокритериальной оптимизации
Постановка задачи
| Определение: |
| Задача многокритериальной оптимизации:
|
Так как не существует единого решение, которое было бы максимальным для всех целевых функций, вместо него можно искать множество множество Парето оптимальных значений.
Множество Парето оптимальных значений
| Определение: |
Множество Парето оптимальных значений:
|
Выражение означает, что доминирует над .
| Определение: |
| Для двух решений и говорят тогда и только тогда, когда - такую пару решений называют недоминируемой |
Множество Парето оптимальных недоминируемых решений называется Парето фронтом.
Получение оптимальных по Парето решений
Для выполнения оптимизации по нескольким критериям мы должны либо заменить единственную целевую