Задача многокритериальной оптимизации. Multiobjectivization

НЕТ ВОЙНЕ

24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян. Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием. Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей. Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить. Антивоенный комитет России

Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению.

meduza.io, Популярная политика, Новая газета, zona.media, Майкл Наки.

Введение

В данной статье рассматривается многокритериальная оптимизация, её задача. Рассматривается понятие Парето-фронт - множество Парето оптимальных значений. Также рассматривается задача коммивояжера и предлагается алгоритм её мультиобъективизации

Задача многокритериальной оптимизации

Постановка задачи

Определение:

Задача многокритериальной оптимизации: [math]maximize \{f(x) = (f_1(x),\dots,f_K(x))\}[/math] [math] x \in X[/math] где [math] f(x) : X \rightarrow R^K[/math] – целевая вектор-функция, где [math]K \ge 2[/math]

Так как не существует единого решение, которое было бы максимальным для всех целевых функций, вместо него можно искать множество [math]X^* \subseteq X [/math] множество Парето оптимальных значений.

Множество Парето оптимальных значений

Определение:

Множество Парето оптимальных значений: [math]\forall x^* \in X^* \not\exists x \in X [/math]:[math]x \succ x^*[/math], где [math]x \succ x^* \Leftrightarrow (\forall i \in 1..K, (f_i(x) \ge f_i(x^*))\land (\exists i \in 1..K, f_i(x) \gt f_i(x^*)))[/math]

Выражение [math]x \succ x^*[/math] означает, что [math]x[/math] доминирует над [math]x^*[/math].

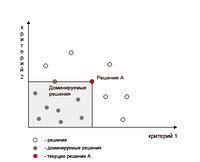
Говорят, что [math]x[/math] доминирует над [math]x^*[/math]. по Парето, если [math]x[/math] не хуже [math]x^*[/math] по всем критериям и хотя бы по одному критерию превосходит [math]x^*[/math]. В таком случае в выборе [math]x^*[/math] нет смысла, т.к. [math]x[/math] по всем параметрам не уступает, а по каким-то и превосхожит [math]x^*[/math]. Если рассматривать всего два критерия то на рис. 1 показана область пространства, доминируемая данным решением А. Эта область «замкнута»: элементы на ее границе также доминируемы А

Рис.1 – Доминируемые решения

Определение:

Для двух решений [math]x[/math] и [math]x'[/math] говорят [math]x \sim x'[/math] тогда и только тогда, когда [math]\exists i \in 1..K \colon f_i(x) \gt f_i(x') \land \exists j \in 1..K, j \ne i \colon f_j(x') \gt f_j(x)[/math] – такую пару решений называют недоминируемой

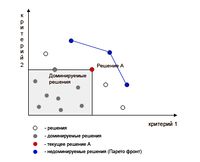
На рис. 2 показана граница Парето для возможных решений в двухкритериальном пространстве

Рис.2 – Парето фронт

Множество Парето оптимальных недоминируемых решений называется Парето фронтом.

Multi-objectivization

Суть метода мульти-объективизации заключается в разбитии сложной задачи с одной целевой функцией на несколько подзадач, найти для каждой подзадачи решение и выбрать оптимальное решение.

Для выполнения оптимизации многокритериальной задачи мы должны добавить в целевую функцию новые параметры, либо должны добавить новые целевые функции.

Сложность этой процедуры заключается в разложении проблемы на ряд мелких независимых между собой подпроблем.

Алгоритмы

Hill-Climbers

Определение:

Hill-Climbers – Итеративный алгоритм, который начинается с произвольного решения проблемы, а затем пытается найти лучшее решение, постепенно изменяя его. Если изменения позволяют найти лучшее решение, алгоритм сохраняет его и повторяет и повторяет своё выполнение до тех пор, пока лучшие решения не могут быть найдены

Initialization:	[math]P \leftarrow \emptyset [/math] Init_pop[math](P)[/math]
Main Loop:	[math]x_1 \leftarrow [/math]Rand_mem[math](P)[/math],[math]x'_2 \leftarrow [/math]Rand_mem[math](P)[/math] [math]x'_1 \leftarrow [/math]Mutate[math](P)[/math],[math]x_2 \leftarrow [/math]Mutate[math](P)[/math] if[math](H(x_1,x'_1)+H(x_2,x'_2) \gt H(x_1,x'_2)+H(x_2,x'_1))[/math] Swap[math](x_1,x'_2)[/math] if [math]f(x'_1) \gt f(x_1)[/math] [math]P \leftarrow P \cup x'_1 \setminus x_1[/math] if [math]f(x'_2) \gt f(x_2)[/math] [math]P \leftarrow P \cup x'_2 \setminus x_2[/math]
Termination:	return Best[math](P)[/math]

Задачи

Hierarchical-if-and-only-if function

H-IIF – предназначена для моделирования проблемы с блочной структурой, каждый блок которой строго связан с остальными блоками.

[math] f(B)= \begin{cases}1,& \mbox{if } |B| = 1, \mbox{ else} \\|B|+f(B_L)+f(B_R),& \mbox{if }(\forall i \{b_i=0\} \mbox{ or } \forall i \{b_i = 1 \}) \\f(B_L) + f(B_R), & \mbox{otherwise} \end{cases} [/math],

где [math]B[/math] – блок бит [math]\{b_1,b_2,\dots,b_n \}, |B|[/math] – размер блока, а [math]B_L, B_R[/math] – левая и правая часть блока соответственно.

Применяя к этой задаче мультиобъективизацию, разобьём задачу [math]f[/math] на [math]k[/math]-задач.

Представим, как будет выглядеть [math]f(B)[/math]:

[math] f(B)= \begin{cases} 0, & \mbox{if } |B| = 1 \mbox{ and }b_1 \neq k, \mbox{ else} \\1,& \mbox{if } |B| = 1 \mbox{ and }b_1 = k, \mbox{ else} \\|B|+f_k(B_L)+f_k(B_R),& \mbox{if }(\forall i \{b_i=k\}), \\f_k(B_L) + f_k(B_R), & \mbox{otherwise} \end{cases} [/math]

где [math]f_0(x)[/math] – первая цель; [math]f_0(x)[/math] – вторая цель.

Данный подход помогает избежать проблему локальных максимумов (минимумов).

Задача коммивояжера

Задача коммивояжера (TSP)является наиболее известно из всего класса [math]NP[/math]-сложных задач. Формулируется задача следующим образом:

Задано [math]C=\{c_1,c_2,\dots,c_N\} [/math] – множество городов и для каждой пары [math]\{c_i,c_j\}[/math] задано расстояние. Наша цель – найти цепь из городов, минимизирующую величину:

[math]\sum^{N-1}_{i=1} d(C_{\pi(i)},C_{\pi(i+1)})+d(C_{\pi(N)},C_{\pi(1)})[/math]

Применяя к этой задаче мультиобъктивизацию, нужно разбить её на подзадачи. TSP – является [math]NP[/math]-сложной именно потому, что нет хорошего разложения этой задачи. Тем не менее задачу можно разбить на две или больше подтуров, каждый из которых мы можем минимизировать.

Представим подтуры в виде двух городов. Тогда наша задача примет вид:

[math]minimize\{f(\pi,a,b) = (f_1(\pi,a,b),f_2(\pi,a,b))\}[/math]

where[math]f_1(\pi,a,b)=\sum^{\pi^{-1}(b)-1}_{i=\pi^{-1}(a)} d(C_{\pi(i)},C_{\pi(i+1)})[/math]

and [math]f_2(\pi,a,b)=\sum^{N-1}_{i=\pi^{-1}(b)} d(C_{\pi(i)},C_{\pi(i+1)}) + \sum^{\pi^{-1}(a)-1}_{i=1} d(C_{\pi(i)},C_{\pi(i+1)}) [/math] [math]+ d(C_{\pi(N)},C_{\pi(1)})[/math],

где [math]a[/math] и [math]b[/math] – два города, указанных априори. Если [math]\pi (a) \lt \pi (b)[/math], меняем их местами.

Предполагается, что [math]a[/math] и [math]b[/math] выбраны произвольно.

Источники

• Википедия: Многокритериальная оптимизация
• Knowles J., Watson R., Corne D. Reducing Local Optima in Single-Objective Problems by Multi-objectivization
• Wikipedia: Multiobjective optimization
• Wikipedia: Hill climbing