Теорема о непринадлежности XOR классу AC⁰ — различия между версиями
Rost (обсуждение | вклад) м (→Теорема) |
Rost (обсуждение | вклад) м (→Теорема) |
||
| Строка 17: | Строка 17: | ||
<tex>\oplus \notin \mathrm{AC^0}</tex>. | <tex>\oplus \notin \mathrm{AC^0}</tex>. | ||
|proof= | |proof= | ||
| − | Рассмотрим произвольную схему из [[Классы NC и AC| класса]] <tex>\mathrm{AC^0}</tex>. Допустим, что эта схема распознает язык <tex>\oplus</tex>. В силу особенности языка <tex>\oplus</tex>, распознающая его схема должна зависить от значений всех своих входов. Однако воспользовавшись леммой, можно с вероятностью, отличной от нуля, представить эту схему в виде <tex>k</tex>-КНФ или <tex>k</tex>-ДНФ, причем <tex>k</tex> не зависит от числа входов схемы. Поскольку рассматриваем схему из класса <tex>\mathrm{AC^0}</tex>, то по определению степень входа не ограничена. | + | Рассмотрим произвольную схему из [[Классы NC и AC| класса]] <tex>\mathrm{AC^0}</tex>. Допустим, что эта схема распознает язык <tex>\oplus</tex>. В силу особенности языка <tex>\oplus</tex>, распознающая его схема должна зависить от значений всех своих входов. Однако воспользовавшись леммой, можно с вероятностью, отличной от нуля, представить эту схему в виде <tex>k</tex>-КНФ или <tex>k</tex>-ДНФ, причем <tex>k</tex> не зависит от числа входов схемы. Поскольку рассматриваем схему из класса <tex>\mathrm{AC^0}</tex>, то по определению степень входа не ограничена. Рассмотрим содержательный случай, когда <tex>k</tex> меньше числа входов схемы. Заметим, что значение <tex>k</tex>-КНФ или <tex>k</tex>-ДНФ можно сделать постоянным, зафиксировав значение не более, чем <tex>k</tex> входов. Для этого достаточно зафиксировать значение лишь одного дизъюнкта или конъюнкта соответственно. Поскольку вероятность представить произвольную схему из класса <tex>\mathrm{AC^0}</tex> в таком виде отлична от нуля, то можно подобрать значения для части входов так, чтобы значение схемы не зависело от оставшихся. А значит, ни одна схема из класса <tex>\mathrm{AC^0}</tex> не распознает язык <tex>\oplus</tex>, поскольку зависит не от всех входных значений. |
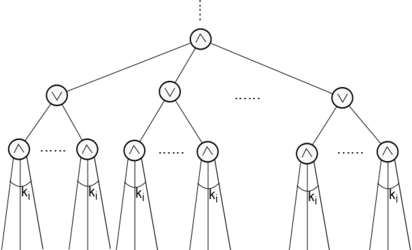
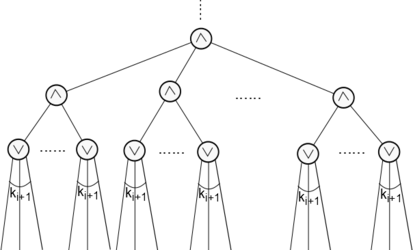
Покажем, как представить схему из класса <tex>\mathrm{AC^0}</tex> в виде <tex>k</tex>-КНФ или <tex>k</tex>-ДНФ. Не умаляя общности, будем считать, что: | Покажем, как представить схему из класса <tex>\mathrm{AC^0}</tex> в виде <tex>k</tex>-КНФ или <tex>k</tex>-ДНФ. Не умаляя общности, будем считать, что: | ||
Версия 14:32, 25 июня 2012
Hastad’s switching lemma
| Лемма: |
Замечание. Для функции можно получить такой же результат, изменив КНФ на ДНФ и наоборот.
Теорема
| Определение: |
| язык над алфавитом , состоящий из слов, содержащих нечетное число |
| Теорема: |
. |
| Доказательство: |
|
Рассмотрим произвольную схему из класса . Допустим, что эта схема распознает язык . В силу особенности языка , распознающая его схема должна зависить от значений всех своих входов. Однако воспользовавшись леммой, можно с вероятностью, отличной от нуля, представить эту схему в виде -КНФ или -ДНФ, причем не зависит от числа входов схемы. Поскольку рассматриваем схему из класса , то по определению степень входа не ограничена. Рассмотрим содержательный случай, когда меньше числа входов схемы. Заметим, что значение -КНФ или -ДНФ можно сделать постоянным, зафиксировав значение не более, чем входов. Для этого достаточно зафиксировать значение лишь одного дизъюнкта или конъюнкта соответственно. Поскольку вероятность представить произвольную схему из класса в таком виде отлична от нуля, то можно подобрать значения для части входов так, чтобы значение схемы не зависело от оставшихся. А значит, ни одна схема из класса не распознает язык , поскольку зависит не от всех входных значений. Покажем, как представить схему из класса в виде -КНФ или -ДНФ. Не умаляя общности, будем считать, что:
Построим итеративный процесс, на каждом шаге которого можно с высокой вероятностью уменьшить глубину схемы на . Пусть глубина схемы, а число входов схемы. Выберем минимальное целое так, чтобы было не меньше, чем число элементов в схеме. Обозначим число входов схемы после -го шага. Возьмем Докажем по индукции, что после -ого шага с достаточно большой вероятностью глубина схемы будет , причем наибольшая степень входа элемента на нижнем уровне не будет превосходить .
|
Источники
- Sanjeev Arora, Boaz Barak. Computational Complexity: A Modern Approach