Теорема о непринадлежности XOR классу AC⁰ — различия между версиями
Rost (обсуждение | вклад) |
Rost (обсуждение | вклад) |
||
| Строка 1: | Строка 1: | ||
{{В разработке}} | {{В разработке}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| Строка 14: | Строка 5: | ||
}} | }} | ||
| + | ===Теорема=== | ||
{{Теорема | {{Теорема | ||
|statement= | |statement= | ||
| Строка 30: | Строка 22: | ||
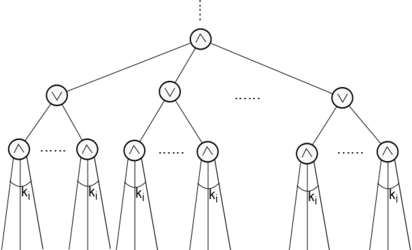
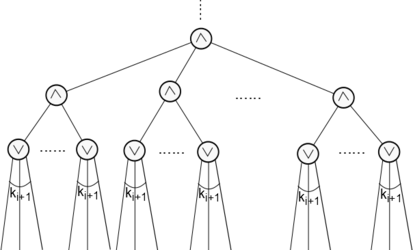
[[Файл:beforeHastadSwitchingTransformation.png|600x250px|thumb|center|Схема на <tex>i</tex>-ом шаге.]] | [[Файл:beforeHastadSwitchingTransformation.png|600x250px|thumb|center|Схема на <tex>i</tex>-ом шаге.]] | ||
| + | |||
| + | ===Hastad’s switching lemma=== | ||
| + | {{Лемма | ||
| + | |statement= | ||
| + | Пусть функция <tex>f(x_1, ...,x_n)</tex> представима в виде <tex>k</tex>-[[ДНФ]], а <tex>p~-</tex> случайное назначение <tex>t</tex> случайно выбранным аргументам случайных значений. Тогда при <tex>s \ge 2</tex> верно, что: <br><tex>P[f|_p</tex> не представима в виде <tex>s</tex>-[[КНФ]]<tex>]\le\left(\frac{(n - t)k^{10}}{n}\right) ^ {s/2}</tex>, где <tex>f|_p</tex> получено при подстановке в функцию <tex>f</tex> значений из <tex>p</tex>. | ||
| + | |proof= | ||
| + | }} | ||
| + | '''Замечание.''' Для функции <tex>\overline{f}</tex> можно получить такой же результат, изменив КНФ на ДНФ и наоборот. | ||
Докажем по индукции, что после <tex>i</tex>-ого шага с достаточно большой вероятностью глубина схемы будет <tex>d - i</tex>, причем наибольшая степень входа элемента на нижнем уровне не будет превосходить <tex>k_i</tex>. | Докажем по индукции, что после <tex>i</tex>-ого шага с достаточно большой вероятностью глубина схемы будет <tex>d - i</tex>, причем наибольшая степень входа элемента на нижнем уровне не будет превосходить <tex>k_i</tex>. | ||
Версия 11:37, 27 июня 2012
| Определение: |
| язык над алфавитом , состоящий из слов, содержащих нечетное число |
Теорема
| Теорема: | ||
. | ||
| Доказательство: | ||
|
Рассмотрим произвольную схему из класса . Допустим, что эта схема распознает язык . В силу особенности языка , распознающая его схема должна зависить от значений всех своих входов. Однако воспользовавшись леммой, можно с вероятностью, отличной от нуля, представить эту схему в виде -КНФ или -ДНФ, причем не зависит от числа входов схемы. Поскольку рассматриваем схему из класса , то по определению степень входа не ограничена. Рассмотрим содержательный случай, когда меньше числа входов схемы. Заметим, что значение -КНФ или -ДНФ можно сделать постоянным, зафиксировав значение не более, чем входов. Для этого достаточно зафиксировать значение лишь одного дизъюнкта или конъюнкта соответственно. Если с вероятностью входу полученной схемы назначается значение, то с вероятностью не менее значение схемы будет постоянным. Поскольку эта вероятность больше нуля, то для произвольной схемы из класса можно подобрать значения части входов так, чтобы значение функции было постоянным, поэтому ни одна схема из этого класса не может распознавать язык . Покажем, как представить схему из класса в виде -КНФ или -ДНФ. Не умаляя общности, будем считать, что:
Построим итеративный процесс, на каждом шаге которого можно с высокой вероятностью уменьшить глубину схемы на . Пусть глубина схемы, а число входов схемы. Выберем минимальное целое так, чтобы было не меньше, чем число элементов в схеме. Обозначим число входов схемы после -го шага. Возьмем Hastad’s switching lemma
Замечание. Для функции можно получить такой же результат, изменив КНФ на ДНФ и наоборот. Докажем по индукции, что после -ого шага с достаточно большой вероятностью глубина схемы будет , причем наибольшая степень входа элемента на нижнем уровне не будет превосходить .
| ||
Источники
- Sanjeev Arora, Boaz Barak. Computational Complexity: A Modern Approach