Теорема Брукса — различия между версиями
Danek g30 (обсуждение | вклад) |
Danek g30 (обсуждение | вклад) (→Теорема) |
||
| Строка 23: | Строка 23: | ||
Если в <tex>G</tex> существует вершина <tex>v</tex> степени <tex> deg\ v < \Delta(G)</tex>, то по выше доказанной лемме <tex> \chi(G) \le \Delta(G)</tex>. То есть осталось рассмотреть случай, когда <tex>G</tex> {{---}} регулярный граф степени <tex>\Delta</tex>. | Если в <tex>G</tex> существует вершина <tex>v</tex> степени <tex> deg\ v < \Delta(G)</tex>, то по выше доказанной лемме <tex> \chi(G) \le \Delta(G)</tex>. То есть осталось рассмотреть случай, когда <tex>G</tex> {{---}} регулярный граф степени <tex>\Delta</tex>. | ||
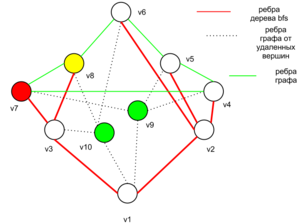
| − | #Если <tex>G</tex> не является двусвязным графом, тогда в графе <tex> G</tex> <tex> \exists</tex> <tex> v \in V</tex>, где v {{---}} точка сочленения. Пусть <tex>G_1,G_2</tex> две компоненты связности полученный при удалении вершины <tex>v</tex>.Тогда, по выше доказанной лемме <tex>G_1,G_2</tex> можно правильно раскрасить в неболее чем <tex>\Delta</tex> цветов.Поскольку количество соседей вершины <tex> v </tex> в каждой из компонент не более <tex> \Delta - 1</tex>, то <tex>G</tex> можно правильно раскрасить в неболее чем <tex>\Delta</tex> цветов. | + | #Если <tex>G</tex> не является вершинно двусвязным графом, тогда в графе <tex> G</tex> <tex> \exists</tex> <tex> v \in V</tex>, где v {{---}} точка сочленения. Пусть <tex>G_1,G_2</tex> две компоненты связности полученный при удалении вершины <tex>v</tex>.Тогда, по выше доказанной лемме <tex>G_1,G_2</tex> можно правильно раскрасить в неболее чем <tex>\Delta</tex> цветов.Поскольку количество соседей вершины <tex> v </tex> в каждой из компонент не более <tex> \Delta - 1</tex>, то <tex>G</tex> можно правильно раскрасить в неболее чем <tex>\Delta</tex> цветов. |
#Если в графе <tex> G</tex> <tex> \exists</tex> <tex> v,u \in V :(u,v) \notin E</tex> и при удалении вершин <tex>v,u</tex> граф теряет связность .Пусть <tex>G_1,G_2</tex> два подграфа <tex> G:G_1 \cap G_2 = \{v,u\} \land G_1 \cup G_2 = G</tex>. Рассмотрим два случая: | #Если в графе <tex> G</tex> <tex> \exists</tex> <tex> v,u \in V :(u,v) \notin E</tex> и при удалении вершин <tex>v,u</tex> граф теряет связность .Пусть <tex>G_1,G_2</tex> два подграфа <tex> G:G_1 \cap G_2 = \{v,u\} \land G_1 \cup G_2 = G</tex>. Рассмотрим два случая: | ||
## Если в одном из подграфов <tex> G_1,G_2</tex> <tex> deg\ u < \Delta - 2 </tex> или <tex> deg\ v < \Delta - 2 </tex> то, подграфы <tex>G_1,G_2</tex> можно правильно раскрасить в неболее чем <tex>\Delta</tex> цветов так, чтобы вершины <tex> u,v </tex> были бы разных цветов.А из этого следует что, граф <tex>G</tex> тоже можно правильно раскрасить в неболее чем <tex>\Delta</tex> цветов. | ## Если в одном из подграфов <tex> G_1,G_2</tex> <tex> deg\ u < \Delta - 2 </tex> или <tex> deg\ v < \Delta - 2 </tex> то, подграфы <tex>G_1,G_2</tex> можно правильно раскрасить в неболее чем <tex>\Delta</tex> цветов так, чтобы вершины <tex> u,v </tex> были бы разных цветов.А из этого следует что, граф <tex>G</tex> тоже можно правильно раскрасить в неболее чем <tex>\Delta</tex> цветов. | ||
Версия 20:59, 13 января 2013
Вспомогательная Лемма
| Лемма: |
Пусть - произвольный связный неориентированный граф и - максимальная степень вершин . Если в таком графе существует вершина степени , то . |
| Доказательство: |
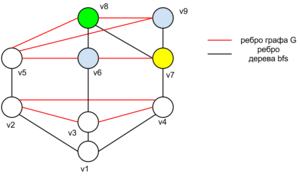
| Запустим алгоритм обхода в ширину из вершины . Пронумеруем вершины где вершина рассмотренная на ом шаге алгоритма bfs. Далее начнем красить вершины в обратном порядке в один из цветов так, чтобы никакое ребро графа не соединяло вершины одного цвета. На ом шаге покраски, для вершины есть не более уже покрашенных соседей, следовательно вершину можно покрасить по крайней мере в один из свободных цветов. Поскольку на каждом шаге алгоритм отработает корректно, следовательно граф можно правильно раскрасить в не более чем цветов, то есть . |
Теорема
| Теорема (Брукса): |
Пусть — связный неориентированный граф и не является или , ни для кого , тогда , где - максимальная степень вершин |
| Доказательство: |
Поэтому мы будем считать до конца доказательства, что . Если в существует вершина степени , то по выше доказанной лемме . То есть осталось рассмотреть случай, когда — регулярный граф степени .
|