Теорема Брукса — различия между версиями
Danek g30 (обсуждение | вклад) (→Теорема) |
|||
| Строка 3: | Строка 3: | ||
|statement= Пусть <tex>G(V,E)</tex> - произвольный связный неориентированный граф и <tex>\Delta(G)</tex> - максимальная степень вершин <tex>G</tex>. Если в таком графе существует вершина <tex>v</tex> степени <tex> deg\ v < \Delta(G)</tex>, то <tex>\chi(G) \le \Delta(G)</tex>. | |statement= Пусть <tex>G(V,E)</tex> - произвольный связный неориентированный граф и <tex>\Delta(G)</tex> - максимальная степень вершин <tex>G</tex>. Если в таком графе существует вершина <tex>v</tex> степени <tex> deg\ v < \Delta(G)</tex>, то <tex>\chi(G) \le \Delta(G)</tex>. | ||
|proof= | |proof= | ||
| − | [[Файл:Brooks_1.png| | + | [[Файл:Brooks_1.png|400px|thumb|Алгоритм расскраски на 5ом шаге]] |
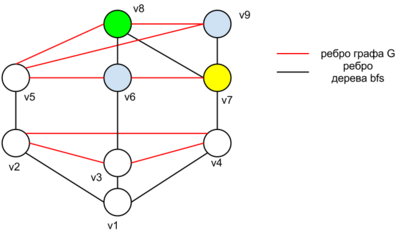
Запустим алгоритм [[Обход в ширину|обхода в ширину]] из вершины <tex>w</tex>. Пронумеруем вершины <tex>v_1,...,v_n,</tex> где <tex>v_i</tex> вершина рассмотренная на <tex>i</tex>ом шаге алгоритма bfs. Далее начнем красить вершины в обратном порядке в один из <tex>\Delta</tex> цветов так, чтобы никакое ребро графа не соединяло вершины одного цвета. На <tex> i</tex>ом шаге покраски, для вершины <tex> v_{n - i+1}</tex> есть не более <tex>\Delta(G) - 1</tex> уже покрашенных соседей, следовательно вершину <tex> v_{n-i+1}</tex> можно покрасить по крайней мере в один из свободных цветов. Поскольку на каждом шаге алгоритм отработает корректно, следовательно граф можно правильно раскрасить в не более чем <tex> \Delta</tex> цветов, то есть <tex> \chi(G) \le \Delta(G)</tex>. | Запустим алгоритм [[Обход в ширину|обхода в ширину]] из вершины <tex>w</tex>. Пронумеруем вершины <tex>v_1,...,v_n,</tex> где <tex>v_i</tex> вершина рассмотренная на <tex>i</tex>ом шаге алгоритма bfs. Далее начнем красить вершины в обратном порядке в один из <tex>\Delta</tex> цветов так, чтобы никакое ребро графа не соединяло вершины одного цвета. На <tex> i</tex>ом шаге покраски, для вершины <tex> v_{n - i+1}</tex> есть не более <tex>\Delta(G) - 1</tex> уже покрашенных соседей, следовательно вершину <tex> v_{n-i+1}</tex> можно покрасить по крайней мере в один из свободных цветов. Поскольку на каждом шаге алгоритм отработает корректно, следовательно граф можно правильно раскрасить в не более чем <tex> \Delta</tex> цветов, то есть <tex> \chi(G) \le \Delta(G)</tex>. | ||
| Строка 30: | Строка 30: | ||
##* <tex>\exists p \in G_2: pu \in E \land pv \in E </tex>, тогда мы можем правильно раскрасить <tex>G_2</tex>, где <tex>deg\ u = deg\ v = 1</tex>, в не более чем <tex> \Delta </tex> цветов так, чтобы вершины <tex>u,v</tex> были одного цвета.Следовательно,можно покрасить граф <tex>G</tex> в не более чем <tex>\Delta</tex> цветов. | ##* <tex>\exists p \in G_2: pu \in E \land pv \in E </tex>, тогда мы можем правильно раскрасить <tex>G_2</tex>, где <tex>deg\ u = deg\ v = 1</tex>, в не более чем <tex> \Delta </tex> цветов так, чтобы вершины <tex>u,v</tex> были одного цвета.Следовательно,можно покрасить граф <tex>G</tex> в не более чем <tex>\Delta</tex> цветов. | ||
##*<tex>\exists u_1,v_1 \in G_2: uu_1 \in E \land vv_1 \in E \land u_1 \neq v_1 </tex>, тогда вместо вершин <tex>\{u,v\}</tex> рассмотрим вершины <tex>\{u,v_1\}</tex>.Заметим, что при удалении этих вершин граф потеряет связность и между ними нет ребра,то есть для этой пары вершин можно провести рассуждения аналогичные тем которые проводились для вершин <tex> v,u</tex>.Из чего, прямым образом вытекает, что граф <tex> G</tex> можно правильно раскрасить в не более чем не более чем <tex>\Delta </tex> цветов. | ##*<tex>\exists u_1,v_1 \in G_2: uu_1 \in E \land vv_1 \in E \land u_1 \neq v_1 </tex>, тогда вместо вершин <tex>\{u,v\}</tex> рассмотрим вершины <tex>\{u,v_1\}</tex>.Заметим, что при удалении этих вершин граф потеряет связность и между ними нет ребра,то есть для этой пары вершин можно провести рассуждения аналогичные тем которые проводились для вершин <tex> v,u</tex>.Из чего, прямым образом вытекает, что граф <tex> G</tex> можно правильно раскрасить в не более чем не более чем <tex>\Delta </tex> цветов. | ||
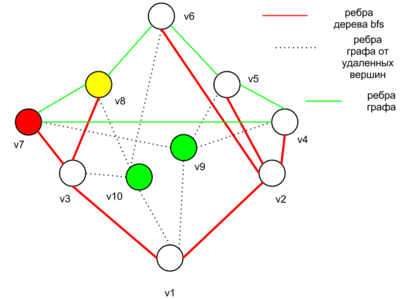
| − | #[[Файл:Brooks_2.png| | + | #[[Файл:Brooks_2.png|400px|thumb|Алгоритм расскраски для 3ого случая на 5ом шаге]]Если вышеописанные случаи не подходят, тогда рассмотрим <tex>w \in V : deg\ w = \Delta</tex>. У вершины <tex>w</tex> должны существовать две соседние вершины <tex>u,v : uv \notin E </tex>, в противном случаи <tex>G = K_n</tex>.Пусть <tex>G_- = G - u - v </tex>. Заметим, что <tex>G_-</tex> связный граф, запустим для <tex>G_-</tex> алгоритм обхода в ширину из вершины <tex>w</tex>. Пронумеруем вершины <tex>v_1,...,v_{n-2},</tex> где <tex>v_i</tex> вершина рассмотренная на <tex>i</tex>ом шаге алгоритма bfs.Теперь пусть <tex> v_{n-1} = v</tex>,и <tex>v_n = u</tex>. Покрасим <tex>v_n,v_{n-1}</tex> в один цвет, далее начнем красить вершины в обратном порядке начиная с <tex>v_{n-2}</tex> в обратном порядке в один из <tex>\Delta</tex> цветов так, чтобы никакое ребро графа не соединяло вершины одного цвета.Заметим, что так всегда можно сделать, поскольку на <tex> i</tex>ом шаге покраски,где <tex>i \neq n</tex>, для вершины <tex> v_{n - i+1}</tex> есть не более <tex>\Delta(G) - 1</tex> уже покрашенных соседей, следовательно вершину <tex> v_{n-i+1}</tex> можно покрасить по крайней мере в один из свободных цветов.Вершину <tex>w</tex>,мы тоже сможем правильно раскрасить в не более чем один из <tex>\Delta</tex> цветов потому, что ее <tex>\Delta</tex> соседей покрашено в не более чем <tex>\Delta - 1</tex> цветов. Таким образом граф <tex> G</tex> можно правильно раскрасить в не более чем не более чем <tex>\Delta</tex> цветов. |
}} | }} | ||
Версия 20:57, 17 января 2013
Вспомогательная Лемма
| Лемма: |
Пусть - произвольный связный неориентированный граф и - максимальная степень вершин . Если в таком графе существует вершина степени , то . |
| Доказательство: |
| Запустим алгоритм обхода в ширину из вершины . Пронумеруем вершины где вершина рассмотренная на ом шаге алгоритма bfs. Далее начнем красить вершины в обратном порядке в один из цветов так, чтобы никакое ребро графа не соединяло вершины одного цвета. На ом шаге покраски, для вершины есть не более уже покрашенных соседей, следовательно вершину можно покрасить по крайней мере в один из свободных цветов. Поскольку на каждом шаге алгоритм отработает корректно, следовательно граф можно правильно раскрасить в не более чем цветов, то есть . |
Теорема
| Теорема (Брукса): |
Пусть — связный неориентированный граф и не является или , ни для кого , тогда , где - максимальная степень вершин |
| Доказательство: |
Поэтому мы будем считать до конца доказательства, что . Если в существует вершина степени , то по выше доказанной лемме . То есть осталось рассмотреть случай, когда — регулярный граф степени .
|