Теорема Брукса — различия между версиями
Danek g30 (обсуждение | вклад) |
Danek g30 (обсуждение | вклад) |
||
| Строка 28: | Строка 28: | ||
### Если сумма степеней вершин <tex>u,v</tex> в одном из подграфов <tex>G_1,G_2</tex> равна <tex>2(\Delta-1)</tex>. Тогда, степени обоих вершин в одном из подграфов равны <tex> \Delta - 1</tex>, рассмотрим например, что в подграфе <tex>G_1</tex>: | ### Если сумма степеней вершин <tex>u,v</tex> в одном из подграфов <tex>G_1,G_2</tex> равна <tex>2(\Delta-1)</tex>. Тогда, степени обоих вершин в одном из подграфов равны <tex> \Delta - 1</tex>, рассмотрим например, что в подграфе <tex>G_1</tex>: | ||
###* Если вершины <tex>u,v</tex> смежны с вершиной <tex>p \in G_2</tex>, тогда мы можем правильно раскрасить <tex>G_2</tex>, где степени вершин <tex>u,v</tex> равны <tex>1</tex>, в не более чем <tex> \Delta </tex> цветов так, чтобы вершины <tex>u,v</tex> были одного цвета. Следовательно, можно покрасить граф <tex>G</tex> в не более чем <tex>\Delta</tex> цветов. | ###* Если вершины <tex>u,v</tex> смежны с вершиной <tex>p \in G_2</tex>, тогда мы можем правильно раскрасить <tex>G_2</tex>, где степени вершин <tex>u,v</tex> равны <tex>1</tex>, в не более чем <tex> \Delta </tex> цветов так, чтобы вершины <tex>u,v</tex> были одного цвета. Следовательно, можно покрасить граф <tex>G</tex> в не более чем <tex>\Delta</tex> цветов. | ||
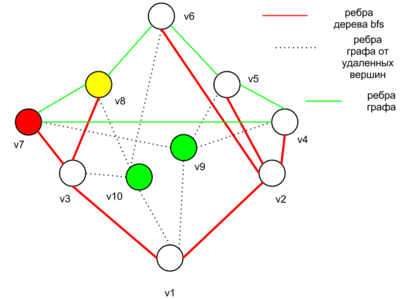
| − | ###*[[Файл:Brooks_2.png|400px|thumb|Алгоритм раскраски. Третий случай, пятый шаг]]Если вершины <tex>u,v</tex> смежны с вершинами <tex>u_1,v_1 \in G_2</tex> соответственно, тогда вместо вершин <tex>\{u,v\}</tex> рассмотрим вершины <tex>\{u,v_1\}</tex>. Заметим, что при удалении этих вершин граф потеряет связность | + | ###*[[Файл:Brooks_2.png|400px|thumb|Алгоритм раскраски. Третий случай, пятый шаг]]Если вершины <tex>u,v</tex> смежны с вершинами <tex>u_1,v_1 \in G_2</tex> соответственно, тогда вместо вершин <tex>\{u,v\}</tex> рассмотрим вершины <tex>\{u,v_1\}</tex>. Заметим, что при удалении этих вершин граф потеряет связность и между ними нет ребра. При этом, сумма степеней новой пары вершин в каждой из компонент, полученных после их удаления, меньше <tex>2(\Delta-1)</tex>. Поэтому, если для этой пары вершин провести рассуждения аналогичные тем, которые проводились для вершин <tex> v,u</tex>, получится, что граф <tex> G</tex> можно правильно раскрасить в не более чем <tex>\Delta </tex> цветов. |
##Если <tex>G</tex> является <tex>k</tex>-связным графом, где <tex>k > 2</tex>. Тогда, рассмотрим <tex>w \in V : deg\ w = \Delta</tex>. У вершины <tex>w</tex> должны существовать две соседние вершины <tex>u,v : uv \notin E </tex>, в противном случае <tex>G = K_n</tex>. Пусть <tex>G_- = G - u - v </tex>. Заметим, что <tex>G_-</tex> связный граф, запустим для <tex>G_-</tex> алгоритм обхода в ширину из вершины <tex>w</tex>. Пронумеруем вершины <tex>v_1,...,v_{n-2}</tex>, где <tex>v_i</tex> вершина рассмотренная на <tex>i</tex>ом шаге алгоритма bfs. Теперь пусть <tex> v_{n-1} = v</tex>, и <tex>v_n = u</tex>. Покрасим <tex>v_n,v_{n-1}</tex> в один цвет, далее начнем красить вершины в обратном порядке, начиная с <tex>v_{n-2}</tex> в один из <tex>\Delta</tex> цветов так, чтобы никакое ребро графа не соединяло вершины одного цвета. Заметим, что так всегда можно сделать, поскольку на <tex> i</tex>ом шаге покраски, где <tex>i \neq n</tex>, для вершины <tex> v_{n - i+1}</tex> есть не более <tex>\Delta(G) - 1</tex> уже покрашенных соседей. Следовательно, вершину <tex> v_{n-i+1}</tex> можно покрасить по крайней мере в один из свободных цветов. Вершину <tex>w</tex> мы тоже сможем правильно раскрасить в один из <tex>\Delta</tex> цветов потому, что ее <tex>\Delta</tex> соседей покрашено в не более чем <tex>\Delta - 1</tex> цветов. Таким образом граф <tex> G</tex> можно правильно раскрасить в не более чем <tex>\Delta</tex> цветов. | ##Если <tex>G</tex> является <tex>k</tex>-связным графом, где <tex>k > 2</tex>. Тогда, рассмотрим <tex>w \in V : deg\ w = \Delta</tex>. У вершины <tex>w</tex> должны существовать две соседние вершины <tex>u,v : uv \notin E </tex>, в противном случае <tex>G = K_n</tex>. Пусть <tex>G_- = G - u - v </tex>. Заметим, что <tex>G_-</tex> связный граф, запустим для <tex>G_-</tex> алгоритм обхода в ширину из вершины <tex>w</tex>. Пронумеруем вершины <tex>v_1,...,v_{n-2}</tex>, где <tex>v_i</tex> вершина рассмотренная на <tex>i</tex>ом шаге алгоритма bfs. Теперь пусть <tex> v_{n-1} = v</tex>, и <tex>v_n = u</tex>. Покрасим <tex>v_n,v_{n-1}</tex> в один цвет, далее начнем красить вершины в обратном порядке, начиная с <tex>v_{n-2}</tex> в один из <tex>\Delta</tex> цветов так, чтобы никакое ребро графа не соединяло вершины одного цвета. Заметим, что так всегда можно сделать, поскольку на <tex> i</tex>ом шаге покраски, где <tex>i \neq n</tex>, для вершины <tex> v_{n - i+1}</tex> есть не более <tex>\Delta(G) - 1</tex> уже покрашенных соседей. Следовательно, вершину <tex> v_{n-i+1}</tex> можно покрасить по крайней мере в один из свободных цветов. Вершину <tex>w</tex> мы тоже сможем правильно раскрасить в один из <tex>\Delta</tex> цветов потому, что ее <tex>\Delta</tex> соседей покрашено в не более чем <tex>\Delta - 1</tex> цветов. Таким образом граф <tex> G</tex> можно правильно раскрасить в не более чем <tex>\Delta</tex> цветов. | ||
}} | }} | ||
Версия 01:19, 20 января 2013
Вспомогательная Лемма
| Лемма: |
Пусть - произвольный связный неориентированный граф и - максимальная степень вершин . Если в таком графе существует вершина степени , то . |
| Доказательство: |
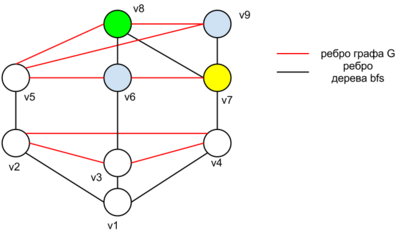
| Запустим алгоритм обхода в ширину из вершины . Пронумеруем вершины где вершина рассмотренная на ом шаге алгоритма bfs. Далее начнем красить вершины в обратном порядке в один из цветов так, чтобы никакое ребро графа не соединяло вершины одного цвета. На ом шаге покраски, для вершины есть не более уже покрашенных соседей (т.к и предок данной вершины в дереве bfs еще не покрашен, а если предка нет, то это вершина и есть ), следовательно вершину можно покрасить по крайней мере в один из свободных цветов. Поскольку на каждом шаге алгоритм отработает корректно, следовательно граф можно правильно раскрасить в не более чем цветов, то есть . |
Теорема
| Теорема (Брукса): |
Пусть — связный неориентированный граф и не является или , ни для кого , тогда , где - максимальная степень вершин |
| Доказательство: |
|
Для доказательства теоремы рассмотрим несколько случаев:
|