Прямое произведение ДКА — различия между версиями
Kris (обсуждение | вклад) м (→Пример) |
Kris (обсуждение | вклад) м (→Пример) |
||
| Строка 24: | Строка 24: | ||
*<tex>\delta(\langle s_1, s_2 \rangle, 0) = \langle \delta_1(s_1, 0), \delta_2(s_2, 0) \rangle = \langle s_1, q_2 \rangle </tex> | *<tex>\delta(\langle s_1, s_2 \rangle, 0) = \langle \delta_1(s_1, 0), \delta_2(s_2, 0) \rangle = \langle s_1, q_2 \rangle </tex> | ||
*<tex>\delta(\langle s_1, q_2 \rangle, 1) = \langle \delta_1(s_1, 1), \delta_2(q_2, 1) \rangle = \langle t_1, t_{21} \rangle </tex> | *<tex>\delta(\langle s_1, q_2 \rangle, 1) = \langle \delta_1(s_1, 1), \delta_2(q_2, 1) \rangle = \langle t_1, t_{21} \rangle </tex> | ||
| + | *<tex>\delta(\langle s_1, t_{21} \rangle, 0) = \langle \delta_1(s_1, 0), \delta_2(t_{21}, 0) \rangle = \langle s_1, q_2 \rangle </tex> | ||
Действительно, заметим, что только слово <tex>01</tex> допускается автоматом <tex>A_1</tex> и <tex>A_2</tex> одновременно. | Действительно, заметим, что только слово <tex>01</tex> допускается автоматом <tex>A_1</tex> и <tex>A_2</tex> одновременно. | ||
Версия 22:39, 8 октября 2014
| Определение: |
| Прямым произведением двух ДКА и называется ДКА , где:
|
Пример
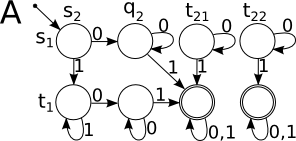
Возьмем автомат допускающий слова , и автомат допускающий слова .
Автомат будет их пересечением.
Согласно определению:
Действительно, заметим, что только слово допускается автоматом и одновременно.
Применение
- С помощью данной конструкции можно построить автомат для пересечения регулярных языков.