Локальные автоматы — различия между версиями
| Строка 11: | Строка 11: | ||
Пусть <tex>G</tex> {{---}} граф Майхилла над алфавитом <tex>\Sigma</tex>. | Пусть <tex>G</tex> {{---}} граф Майхилла над алфавитом <tex>\Sigma</tex>. | ||
| − | Символ <tex>c</tex> | + | Символ <tex>c</tex>, <tex>c \in \Sigma</tex>, назовем разрешенным, если им помечена вершина, являющая одновременно начальной и конечной. |
Не пустая строка <tex>c_1c_2...c_n</tex> из <tex>\Sigma^*</tex> длиной не менее двух символов, называется разрешенной, если символом <tex>c_1</tex> отмечена стартовая вершина, а символом <tex>c_n</tex> {{---}} конечная, и для всех <tex>1 \leqslant i \leqslant n - 1</tex> в <tex>G</tex> существует ребро <tex>a_i \rightarrow a_{i+1}</tex>. | Не пустая строка <tex>c_1c_2...c_n</tex> из <tex>\Sigma^*</tex> длиной не менее двух символов, называется разрешенной, если символом <tex>c_1</tex> отмечена стартовая вершина, а символом <tex>c_n</tex> {{---}} конечная, и для всех <tex>1 \leqslant i \leqslant n - 1</tex> в <tex>G</tex> существует ребро <tex>a_i \rightarrow a_{i+1}</tex>. | ||
| Строка 44: | Строка 44: | ||
* Отметим конечные вершины как терминальные состояния. | * Отметим конечные вершины как терминальные состояния. | ||
* Отметим каждое ребро результирующего ориентированного графа символом, стоящим в вершине, на которою оно указывает. | * Отметим каждое ребро результирующего ориентированного графа символом, стоящим в вершине, на которою оно указывает. | ||
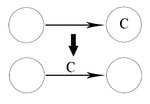
| + | Переходы преобразуются следующим образом: [[Файл:Myhill1.png|150px]] | ||
| + | |||
По построению стартовое состояние не является терминальным. | По построению стартовое состояние не является терминальным. | ||
Версия 17:15, 2 января 2015
| Определение: |
| Граф Майхилла (над алфавитом ) (англ. Myhill graph) — ориентированный граф, удовлетворяющий свойствам:
1. Для каждой упорядоченной пары вершин и существует только одно ребро из в . 2. Некоторые вершины обозначены начальными, а некоторые - конечными. Ребро может одновременно быть начальным и конечным. 3. Вершины обозначены различными символами из конечного алфавита , то есть мы можем обращаться к вершине по ее символу. |
Пусть — граф Майхилла над алфавитом .
Символ , , назовем разрешенным, если им помечена вершина, являющая одновременно начальной и конечной.
Не пустая строка из длиной не менее двух символов, называется разрешенной, если символом отмечена стартовая вершина, а символом — конечная, и для всех в существует ребро .
Язык , распознаваемый графом Майхилла, состоит из всех разрешенных строк из .
Покажем, графы Майхилла могут быть представлены в виде автоматов. Пусть — ДКА, не обязательно законченный.
| Определение: |
| Автомат называется локальным (англ. local automation), если для любого из множество содержит не более одного элемента. |
| Определение: |
| Автомат называется стандартным локальным автоматом (англ. standard loal automation), если в нем нет перехода в начальное состояние. |
Таким образом, автомат является локальным, если для каждого из нет переходов, отмеченных , или если все они в одно состояние.
Покажем, что граф Майхилла может быть преобразован в стандартный локальный автомат таким образом, что распознаваемый им язык не изменится.