АВЛ-дерево — различия между версиями
(→Балансировка) |
Анна (обсуждение | вклад) (→Операции) |
||
| Строка 123: | Строка 123: | ||
[[File:avl_u4.jpg|300px]] | [[File:avl_u4.jpg|300px]] | ||
| + | |||
| + | ===Алгоритм разделения AVL-дерева на два=== | ||
| + | ====Алгоритм первый==== | ||
| + | Пусть у нас есть дерево <tex>T</tex>. Мы должны разбить его на два дерева <tex>T_{1}</tex> и <tex>T_{2}</tex> такие, что <tex>T_{1} \leqslant x</tex> и <tex>x < T_{2}</tex>. | ||
| + | |||
| + | Предположим, что корень нашего дерева <tex>\leqslant x</tex>, в таком случае все левое поддерево вместе с корнем после разделения отойдет в дерево <tex>T_{1}</tex>. Тогда рекурсивно спускаемся в правое поддерево и там проверяем это условие (так как часть правого поддерева тоже может содержать ключи <tex>\leqslant x</tex>). Если же корень оказался <tex>> x</tex>, то мы спускаемся той же рекурсией, но только в левое поддерево и ищем там. | ||
| + | |||
| + | Пусть мы пришли в поддерево <tex>S</tex>, корень которого <tex>\leqslant x</tex>. В таком случае этот корень со своим левым поддеревом должен отойти в дерево <tex>T_{1}</tex>. Поэтому мы делаем следующее: запоминаем ссылку на правое поддерево <tex>S</tex>, удаляем корень, запоминая его значение (не меняя конфигурацию дерева, то есть просто делаем ссылки на него NULL'ами). Таким образом, мы отделяем сбалансированное АВЛ-дерево (бывшее левое поддерево <tex>S</tex>). Делаем новую вершину со значением бывшего корня правым листом самой правой вершины <tex>S</tex> и запускаем балансировку. Обозначим полученное дерево за <tex>T'</tex>. Теперь нам нужно объединить его с уже построенным ранее <tex>T_{1}</tex> (оно может быть пустым, если мы первый раз нашли такое дерево <tex>S</tex>). Для этого мы ищем в дереве <tex>T_{1}</tex> самое правое поддерево <tex>P</tex> высоты, равной высоте <tex>T'</tex> (спускаясь от корня всегда в правые поддеревья). Делаем новое дерево <tex>K</tex>, сливая <tex>P</tex> и <tex>T'</tex> (очевидно, все ключи в <tex>T_{1}</tex> меньше ключей в <tex>T'</tex>, поэтому мы можем это сделать). Теперь в дереве <tex>T_{1}</tex> у отца вершины, в которой мы остановились при поиске дерева <tex>P</tex>, правым поддеревом делаем дерево <tex>K</tex> и запускаем балансировку. После нужно спуститься в правое поддерево бывшего дерева <tex>S</tex> (по ссылке, которую мы ранее запомнили) и обработать его. | ||
| + | |||
| + | Если мы пришли в поддерево <tex>Q</tex>, корень которого <tex>> x</tex>, совершаем аналогичные действия: делаем NULL'ами ссылки на корень <tex>Q</tex>, запоминая ссылку на его левое поддерево. Делаем новую вершину со значением бывшего корня левым листом самой левой вершины <tex>Q</tex> и запускаем балансировку. Объединяем полученное АВЛ-дерево с уже построенным ранее <tex>T_{2}</tex> аналогичным первому случаю способом, только теперь мы ищем самое левое поддерево <tex>T_{2}</tex>. | ||
| + | |||
| + | Рассмотри пример (рис. 1). Цветом выделены поддеревья, которые после разделения должны отойти в дерево <tex>T_{1}</tex>. <tex>x = 76</tex>. | ||
| + | |||
| + | {| cellpadding="2" | ||
| + | | || [[Файл:AVL.jpg|thumb|left|525px|Рис. 1. Разделение АВЛ-дерева на два.]] | ||
| + | |} | ||
| + | |||
| + | Корень дерева <tex>\leqslant x</tex>, поэтому он со всем выделенным поддеревом должен отойти в дерево <tex>T_{1}</tex>. По описанному выше алгоритму отделяем это поддерево с корнем и делаем из них сбалансированное АВЛ-дерево <tex>T'</tex> (рис. 2). Так как это первая ситуация, в которой корень рассматриваемого поддерева был <tex>\leqslant x</tex>, <tex>T'</tex> становится <tex>T_{1}</tex>. Далее по сохраненной ссылке спускаемся в правое поддерево. Его корень <tex>> x</tex>. Следовательно, строим из него и его правого поддерева <tex>T_{2}</tex> и спускаемся в левое поддерево. Снова корень <tex>\leqslant x</tex>. Строим новое <tex>T'</tex> и объединяем его с уже существующим <tex>T_{1}</tex> (рис. 3). | ||
| + | |||
| + | {| cellpadding="2" | ||
| + | | || [[Файл:АВВЛ2.jpg|thumb|left|525px|Рис. 2. Создание T'.]] | ||
| + | |} | ||
| + | {| cellpadding="2" | ||
| + | | || [[Файл:AVL3.jpg|thumb|left|1250px|Рис. 3. Объединение T' и T1.]] | ||
| + | |} | ||
| + | |||
| + | Далее действуем по алгоритму и в итоге получаем (рис. 4): | ||
| + | |||
| + | {| cellpadding="2" | ||
| + | | || [[Файл:End.jpg|thumb|left|525px|Рис. 4. АВЛ-деревья после разделения.]] | ||
| + | |} | ||
| + | |||
| + | Данный алгоритм имеет сложность <tex>O(\log^{2} n)</tex>. | ||
| + | |||
| + | ====Алгоритм второй==== | ||
| + | Рассмотрим решение, которое имеет сложность <tex>O(\log{n})</tex>. | ||
| + | |||
| + | Вернемся к примеру (рис. 1). Теперь рекурсивно спустимся вниз и оттуда будем строить деревья <tex>T_{1}</tex> и <tex>T_{2}</tex>, передавая наверх корректные АВЛ-деревья. То есть для рис. 1 первым в дерево <tex>T_{1}</tex> придет вершина <tex>75</tex> с левым поддеревом (выделено светло-зеленым цветом), так как это корректное АВЛ-дерево, оно же и вернется из рекурсии. Далее мы попадем в вершину со значением <tex>70</tex> и должны слить ее и ее левое поддерево (выделено светло-синим) с тем, что нам пришло. И сделать это нужно так, чтобы передать наверх корректное АВЛ-дерево. Будем действовать по такому алгоритму, пока не дойдем до вершины. | ||
| + | |||
| + | Пусть мы пришли в поддерево <tex>S</tex> с корнем <tex>\leqslant x</tex>. Тогда сольем его с уже построенным на тот момент <tex>T_{1}</tex> (<tex>T_{1}</tex> пришло снизу, а значит по условию рекурсии это корректное АВЛ-дерево, <tex>S \leqslant T_{1}</tex> и <tex>h(T_{1}) \leqslant h(S)</tex>). Но так как обычная процедура слияния сливает два АВЛ-дерева, а <tex>S</tex> не является корректным АВЛ-деревом, мы немного ее изменим. Пусть мы в дереве <tex>S</tex> нашли самое правое поддерево <tex>K</tex>, высота которого равна высоте <tex>T_{1}</tex>. Тогда сделаем новое дерево <tex>T'</tex>, корнем которого будет вершина <tex>S</tex> (без нее это дерево является сбалансированным), правым поддеревом {{---}} <tex>T_{1}</tex>, левым {{---}} <tex>K</tex>. И подвесим <tex>T'</tex> на то место, где мы остановились при поиске <tex>K</tex>. Запустим балансировку. В случае, когда корень поддерева, в которое мы пришли, <tex>> x</tex>, все аналогично. | ||
| + | |||
| + | Разберем пример на рис. 1. Пусть мы рекурсивно спустились до узла <tex>77</tex>. Ключ больше <tex>x</tex>, поэтому эта вершина станет деревом <tex>T_{2}</tex> и передастся наверх. Теперь мы поднялись в узел <tex>75</tex>. Он со своим левым поддеревом станет деревом <tex>T_{1}</tex> и мы снова поднимемся наверх в узел <tex>70</tex>. Он со своим левым поддеревом снова должен отойти в дерево <tex>T_{1}</tex>, и так как теперь дерево <tex>T_{1}</tex> уже не пустое, то их надо слить. После слияния по описанному выше алгоритму получим (рис. 5) | ||
| + | |||
| + | {| cellpadding="2" | ||
| + | | || [[Файл:Ex.jpg|thumb|left|525px|Рис. 5.]] | ||
| + | |} | ||
| + | |||
| + | После мы поднимемся в вершину с ключом <tex>80</tex>. Она с правым поддеревом отойдет в дерево <tex>T_{2}</tex> (рис. 6). | ||
| + | |||
| + | {| cellpadding="2" | ||
| + | | || [[Файл:Ex2am.jpg|thumb|left|525px|Рис. 6.]] | ||
| + | |} | ||
| + | |||
| + | И на последней итерации мы поднимемся в корень дерева с ключом <tex>50</tex>, он с левым поддеревом отойдет в дерево <tex>T_{1}</tex>, после чего алгоритм завершится. | ||
| + | |||
| + | Пусть поддеревьев с ключами <tex>\leqslant x</tex> оказалось больше, чем поддеревьев с ключами <tex>> x</tex>. Докажем для них логарифмическую асимптотику. Дерево на последнем уровне имеет высоту <tex>H_{k}</tex> (она может быть не равна <tex>1</tex>, если мы придём в <tex>x</tex>). Его мы передаем наверх и вставляем в поддерево высотой <tex>H_{k-1}</tex>. <tex>H_{k} \leqslant H_{k-1}</tex>, так как разница высот поддеревьев у любой вершины не больше <tex>1</tex>, и мы при переходе от <tex>H_{k}</tex> к <tex>H_{k-1}</tex> поднимаемся как минимум на одну вершину вверх. Слияние этих поддеревьев мы выполним за <tex>H_{k-1} - H_{k}</tex>, получим в итоге дерево высоты не большей, чем <tex>H_{k-1}</tex>. Его мы передадим наверх, поэтому в следующий раз слияние будет выполнено за <tex>H_{k-2} - H_{k - 1}</tex> и так далее. Таким образом мы получим <tex>(H - H_{1}) + (H_{1} - H_{2}) + (H_{2} - H_{3}) + \cdots + (H_{k - 1} - H_{k}) = H - H_{k} = O(\log{n})</tex>. | ||
| + | |||
| + | Итоговая асимптотика алгоритма {{---}} <tex>O(\log{n})</tex>. | ||
== Ссылки == | == Ссылки == | ||
Версия 21:40, 2 июня 2015
АВЛ-дерево (AVL-Tree) — сбалансированное двоичное дерево поиска, в котором поддерживается следующее свойство: для каждой его вершины высота её двух поддеревьев различается не более чем на 1.
АВЛ-деревья названы по первым буквам фамилий их изобретателей, Г. М. Адельсона-Вельского и Е. М. Ландиса, которые впервые предложили использовать АВЛ-деревья в 1962 году.
Содержание
Высота дерева
| Теорема: | ||||||
АВЛ-дерево с ключами имеет высоту . | ||||||
| Доказательство: | ||||||
|
Высоту поддерева с корнем будем обозначать как , высоту поддерева — как .
Логарифмируя по основанию , получаем Таким образом, получаем, что высота AVL-дерева из n вершин — . | ||||||
Балансировка
Балансировкой вершины называется операция, которая в случае разницы высот левого и правого поддеревьев , изменяет связи предок-потомок в поддереве данной вершины так, чтобы восстановилось свойство дерева , иначе ничего не меняет. Для балансировки будем хранить для каждой вершины разницу между высотой её левого и правого поддерева
Для балансировки вершины используются один из 4 типов вращений:
| Тип вращения | Иллюстрация | Когда используется | Расстановка балансов |
|---|---|---|---|
| Малое левое вращение (Small left rotation) | 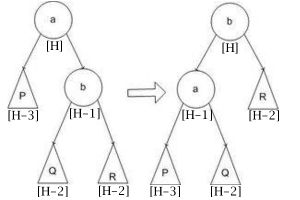
|
и или и . |
|
| Большое левое вращение (Big left rotation) | 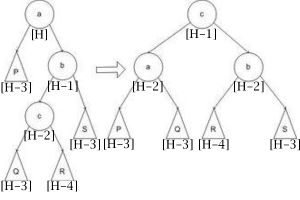
|
, и или , и или , и . |
|
Малое правое и большое правое вращение определяются симметрично малому левому и большому левому вращению. В каждом случае операция приводит к нужному результату, а полная высота уменьшается не более чем на 1 и не может увеличиться.
Все операции вращения, очевидно, требуют операций.
Операции
Добавление вершины
Пусть нам надо добавить ключ . Будем спускаться по дереву, как при поиске ключа . Если мы стоим в вершине и нам надо идти в поддерево, которого нет, то делаем ключ листом, а вершину его корнем. Дальше поднимаемся вверх по пути поиска и пересчитываем баланс у вершин. Если мы поднялись в вершину из левого поддерева, то увеличивается на единицу, если из правого, то уменьшается на единицу. Если пришли в вершину и её баланс стал равным нулю, то это значит высота поддерева не изменилась и подъём останавливается. Если пришли в вершину и её баланс стал равным или , то это значит высота поддерева изменилась и подъём продолжается. Если пришли в вершину и её баланс стал равным или , то делаем одно из четырёх вращений и, если после вращения баланс стал равным нулю, то останавливаемся, иначе продолжаем подъём.
Так как в процессе добавления вершины мы рассматриваем не более, чем вершин дерева, и для каждой запускаем балансировку не более одного раза, то суммарное количество операций при включении новой вершины в дерево составляет операций.
Удаление вершины
Для простоты опишем рекурсивный алгоритм удаления. Если вершина - лист, то удалим её, иначе найдём самую близкую по значению вершину , переместим её на место удаляемой вершины и удалим вершину . От удалённой вершины будем подниматься вверх к корню и пересчитывать баланс у вершин. Если мы поднялись в вершину из левого поддерева, то уменьшается на единицу, если из правого, то увеличивается на единицу. Если пришли в вершину и её баланс стал равным или , то это значит, что высота этого поддерева не изменилась и подъём можно остановить. Если баланс вершины стал равным нулю, то высота поддерева уменьшилась и подъём нужно продолжить. Если баланс стал равным или , следует выполнить одно из четырёх вращений и, если после вращений баланс вершины стал равным нулю, то подъём продолжается, иначе останавливается.
В результате указанных действий на удаление вершины и балансировку суммарно тратится, как и ранее, операций. Таким образом, требуемое количество действий — .
Поиск вершины, минимум/максимум в дереве, etc.
Остальные операции не меняют структуры дерева, поэтому выполняются так же, как и в наивной реализации дерева поиска.
Слияние двух AVL-деревьев
Дано два дерева и , все ключи в меньше ключей в , .
В дереве удаляем самую правую вершину, назовём её . Высота дерева может уменьшиться на единицу. В дереве идём от корня всегда в левое поддерево и, когда высота этого поддерева будет равна высоте дерева , делаем новое дерево , корнем будет вершина , левым поддеревом будет дерево , а правым дерево . Теперь в дереве у вершины, в которой мы остановились при спуске, левым поддеревом делаем дерево и запускаем балансировку. Таким образом, дерево будет результатом слияния двух АВЛ-деревьев.
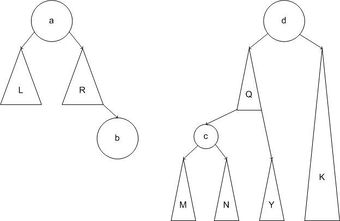
Дерево и до слияния
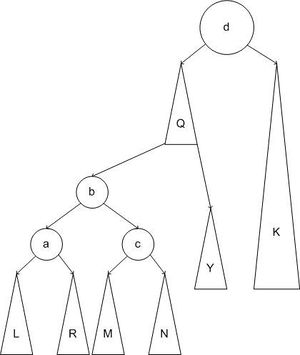
Дерево после слияния
Алгоритм разделения AVL-дерева на два
Алгоритм первый
Пусть у нас есть дерево . Мы должны разбить его на два дерева и такие, что и .
Предположим, что корень нашего дерева , в таком случае все левое поддерево вместе с корнем после разделения отойдет в дерево . Тогда рекурсивно спускаемся в правое поддерево и там проверяем это условие (так как часть правого поддерева тоже может содержать ключи ). Если же корень оказался , то мы спускаемся той же рекурсией, но только в левое поддерево и ищем там.
Пусть мы пришли в поддерево , корень которого . В таком случае этот корень со своим левым поддеревом должен отойти в дерево . Поэтому мы делаем следующее: запоминаем ссылку на правое поддерево , удаляем корень, запоминая его значение (не меняя конфигурацию дерева, то есть просто делаем ссылки на него NULL'ами). Таким образом, мы отделяем сбалансированное АВЛ-дерево (бывшее левое поддерево ). Делаем новую вершину со значением бывшего корня правым листом самой правой вершины и запускаем балансировку. Обозначим полученное дерево за . Теперь нам нужно объединить его с уже построенным ранее (оно может быть пустым, если мы первый раз нашли такое дерево ). Для этого мы ищем в дереве самое правое поддерево высоты, равной высоте (спускаясь от корня всегда в правые поддеревья). Делаем новое дерево , сливая и (очевидно, все ключи в меньше ключей в , поэтому мы можем это сделать). Теперь в дереве у отца вершины, в которой мы остановились при поиске дерева , правым поддеревом делаем дерево и запускаем балансировку. После нужно спуститься в правое поддерево бывшего дерева (по ссылке, которую мы ранее запомнили) и обработать его.
Если мы пришли в поддерево , корень которого , совершаем аналогичные действия: делаем NULL'ами ссылки на корень , запоминая ссылку на его левое поддерево. Делаем новую вершину со значением бывшего корня левым листом самой левой вершины и запускаем балансировку. Объединяем полученное АВЛ-дерево с уже построенным ранее аналогичным первому случаю способом, только теперь мы ищем самое левое поддерево .
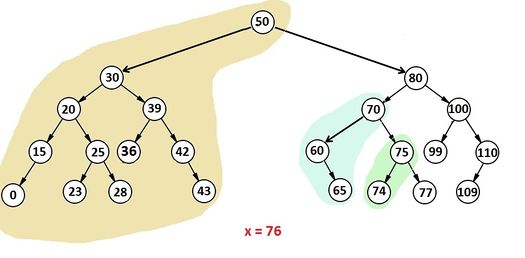
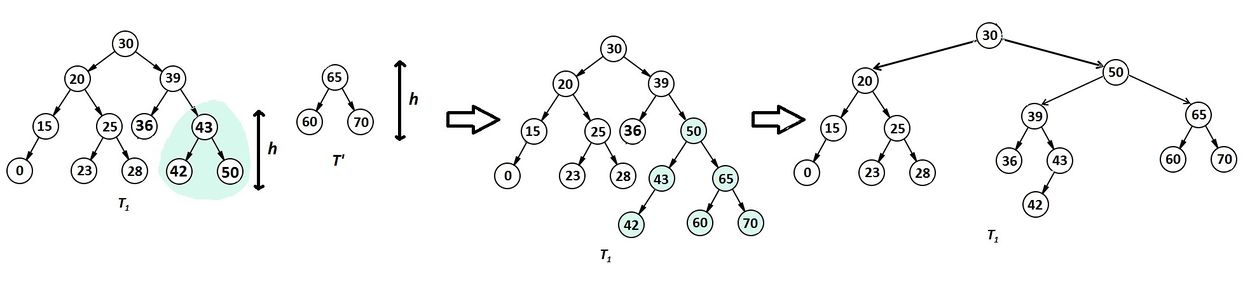
Рассмотри пример (рис. 1). Цветом выделены поддеревья, которые после разделения должны отойти в дерево . .
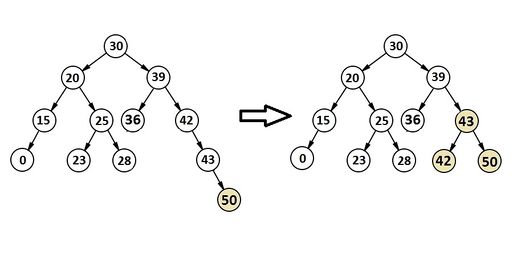
Корень дерева , поэтому он со всем выделенным поддеревом должен отойти в дерево . По описанному выше алгоритму отделяем это поддерево с корнем и делаем из них сбалансированное АВЛ-дерево (рис. 2). Так как это первая ситуация, в которой корень рассматриваемого поддерева был , становится . Далее по сохраненной ссылке спускаемся в правое поддерево. Его корень . Следовательно, строим из него и его правого поддерева и спускаемся в левое поддерево. Снова корень . Строим новое и объединяем его с уже существующим (рис. 3).
Далее действуем по алгоритму и в итоге получаем (рис. 4):
Данный алгоритм имеет сложность .
Алгоритм второй
Рассмотрим решение, которое имеет сложность .
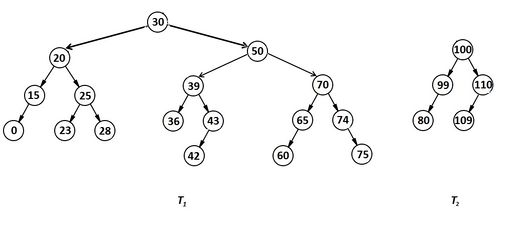
Вернемся к примеру (рис. 1). Теперь рекурсивно спустимся вниз и оттуда будем строить деревья и , передавая наверх корректные АВЛ-деревья. То есть для рис. 1 первым в дерево придет вершина с левым поддеревом (выделено светло-зеленым цветом), так как это корректное АВЛ-дерево, оно же и вернется из рекурсии. Далее мы попадем в вершину со значением и должны слить ее и ее левое поддерево (выделено светло-синим) с тем, что нам пришло. И сделать это нужно так, чтобы передать наверх корректное АВЛ-дерево. Будем действовать по такому алгоритму, пока не дойдем до вершины.
Пусть мы пришли в поддерево с корнем . Тогда сольем его с уже построенным на тот момент ( пришло снизу, а значит по условию рекурсии это корректное АВЛ-дерево, и ). Но так как обычная процедура слияния сливает два АВЛ-дерева, а не является корректным АВЛ-деревом, мы немного ее изменим. Пусть мы в дереве нашли самое правое поддерево , высота которого равна высоте . Тогда сделаем новое дерево , корнем которого будет вершина (без нее это дерево является сбалансированным), правым поддеревом — , левым — . И подвесим на то место, где мы остановились при поиске . Запустим балансировку. В случае, когда корень поддерева, в которое мы пришли, , все аналогично.
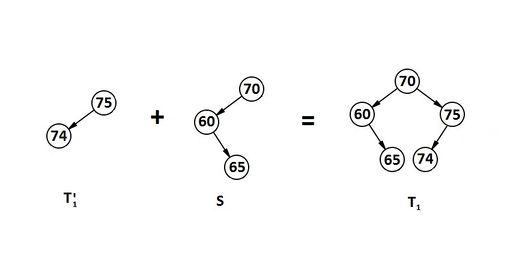
Разберем пример на рис. 1. Пусть мы рекурсивно спустились до узла . Ключ больше , поэтому эта вершина станет деревом и передастся наверх. Теперь мы поднялись в узел . Он со своим левым поддеревом станет деревом и мы снова поднимемся наверх в узел . Он со своим левым поддеревом снова должен отойти в дерево , и так как теперь дерево уже не пустое, то их надо слить. После слияния по описанному выше алгоритму получим (рис. 5)
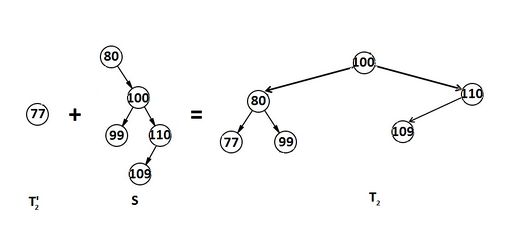
После мы поднимемся в вершину с ключом . Она с правым поддеревом отойдет в дерево (рис. 6).
И на последней итерации мы поднимемся в корень дерева с ключом , он с левым поддеревом отойдет в дерево , после чего алгоритм завершится.
Пусть поддеревьев с ключами оказалось больше, чем поддеревьев с ключами . Докажем для них логарифмическую асимптотику. Дерево на последнем уровне имеет высоту (она может быть не равна , если мы придём в ). Его мы передаем наверх и вставляем в поддерево высотой . , так как разница высот поддеревьев у любой вершины не больше , и мы при переходе от к поднимаемся как минимум на одну вершину вверх. Слияние этих поддеревьев мы выполним за , получим в итоге дерево высоты не большей, чем . Его мы передадим наверх, поэтому в следующий раз слияние будет выполнено за и так далее. Таким образом мы получим .
Итоговая асимптотика алгоритма — .