Обсуждение участника:Novik — различия между версиями
Novik (обсуждение | вклад) м (→Поиск максимального целого поддерева, являющегося деревом поиска) |
Novik (обсуждение | вклад) м (→Поиск максимального целого поддерева, являющегося деревом поиска) |
||
| Строка 20: | Строка 20: | ||
===Поиск максимального целого поддерева, являющегося деревом поиска=== | ===Поиск максимального целого поддерева, являющегося деревом поиска=== | ||
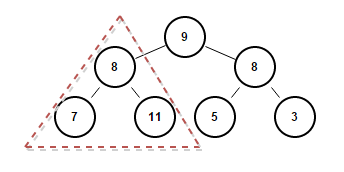
| + | [[Файл:ЗадачаЦелый.PNG|400px|thumb|right|Ответ на задачу выделен пунктиром]] | ||
| + | |||
Решение этой задачи легко получить из предыдущей. Будем проверять все поддеревья и из тех, что окажутся деревом поиска, выберем максимальное. Под размером дерева подразумевается количество вершин в нем. | Решение этой задачи легко получить из предыдущей. Будем проверять все поддеревья и из тех, что окажутся деревом поиска, выберем максимальное. Под размером дерева подразумевается количество вершин в нем. | ||
| Строка 25: | Строка 27: | ||
Глобальная переменная '''ans''' хранит ссылку на корень текущего максимально поддерева поиска. | Глобальная переменная '''ans''' хранит ссылку на корень текущего максимально поддерева поиска. | ||
| − | <code> | + | <code style = "display: inline-block;"> |
'''boolean''' isSearchTree(Node v): | '''boolean''' isSearchTree(Node v): | ||
'''if''' (v.l == null && v.r == null) <font color = "green">// Если текущая вершина - лист</font> | '''if''' (v.l == null && v.r == null) <font color = "green">// Если текущая вершина - лист</font> | ||
Версия 22:36, 26 мая 2015
Содержание
Двоичное дерево поиска
Проверка двоичного дерева на инвариант дерева поиска
Дано произвольное двоичное дерево и необходимо узнать является ли оно деревом поиска. Чтобы дерево было деревом поиска достаточно выполнение следующих условий для всех вершин:
- правое и левое поддеревья являются деревьями поиска,
- максимум в левом поддереве меньше значения в текущей вершине, а минимум в правом больше.
Псевдокод
Для решения этой задачи нам понадобятся стандартные функции getMax и getMin, которые возвращают максимум и минимум в дереве поиска соответственно.
boolean isSearchTree(Node v):
if (v.l == null && v.r == null) // Если текущая вершина - лист
return true;
if (isSearchTree(v.l) && isSearchTree(v.r) && getMax(v.l) < v.val && getMin(v.r) > v.val)
// getMax и getMin запускаются только, если оба поддерева являются деревьями поиска
return true; // Поддерево является деревом поиска
else
return false;
Поиск максимального целого поддерева, являющегося деревом поиска
Решение этой задачи легко получить из предыдущей. Будем проверять все поддеревья и из тех, что окажутся деревом поиска, выберем максимальное. Под размером дерева подразумевается количество вершин в нем.
Псевдокод
Глобальная переменная ans хранит ссылку на корень текущего максимально поддерева поиска.
boolean isSearchTree(Node v):
if (v.l == null && v.r == null) // Если текущая вершина - лист
v.max = v.val;
v.min = v.val;
v.size = 1;
if (1 > currMaxSize)
ans = v;
currMaxSize = 1;
return true;
if (isSearchTree(v.l) && isSearchTree(v.r) && v.l.max < v.val && v.r.min > v.val)
v.max = v.r.max;
v.min = v.l.min;
v.size = v.l.size + v.r.size + 1;
if (v.size > currMaxSize)
ans = v;
currMaxSize = v.size;
return true;
else
v.size = 1;
return false;
Поиск максимального поддерева, являющегося деревом поиска
В этой задаче нам не требуется найти целое дерево, то есть у любой в таком дереве вершины может не быть одного из поддеревьев. Тогда для решения проверку левого и правого поддеревьев надо сделать отдельно.
Псевдокод
boolean isSearchTree(Node v):
v.max = v.val;
v.min = v.val;
boolean flag = false; // true - дерево является деревом поиска, false - нет - лист
v.size = 1;
if (v.l == null && v.r == null) // Если текущая вершина - лист
if (1 > currMaxSize)
ans = v;
currMaxSize = 1;
return true;
if (isSearchTree(v.l) && v.l.max < v.val)
v.min = v.l.min;
v.size += v.l.size;
flag = true;
if (isSearchTree(v.r) && v.r.min > v.val)
v.max = v.r.max;
v.size += v.r.size;
flag = true;
if (flag && v.size > currMaxSize)
ans = v;
currMaxSize = v.size;
if (flag)
return true;
else
v.size = 1;
return false;