Персистентный стек

Алгоритм

 struct Node:
   T value // Значение в узле
   Node prev // Ссылка на прошлую версию

Реализация на массиве

Заведем массив запросов, модифицирующих стек.
У каждого элемента массива будет [math]2[/math] поля: значение в вершине стека и индекс предыдущей версии стека.
Тогда операции push и pop будут иметь следующий вид:

• [math] \mathrm{push}(i, x)[/math] — добавляет элемент [math]x[/math] в стек с номером [math]i[/math], результирующий стек будет иметь номер [math] n + 1 [/math],

 function push(i : uint, x : T):
   s.top = s.top + 1
   s[s.top].value = x
   s[s.top].prev = i 

• [math]\mathrm{pop}(i)[/math] — возвращает значение, хранящееся в элементе с номером [math]i[/math] и копирует элемент, предыдущий для него,

результирующий стек будет иметь номер [math] n + 1 [/math].

 T pop(i : uint):
   Node k = s[i]
   k = s[k.prev]
   push(k.prev, k.value)
   return s[i].value

Реализация на списке

Будем хранить состояния в узлах. Будем возвращать пользователю информацию о текущей вершине.
У каждого узла будет [math]2[/math] поля: значение в вершине стека и ссылка на предыдущую версию стека.

• [math] \mathrm{push}(i, x)[/math] — добавляет элемент [math]x[/math] в стек узла [math]i[/math],

 Stack push(i : Node, x : T):
   k.value = x
   k.prev = i
   s.top = k
   return s

• [math]\mathrm{pop}(i)[/math] — возвращает значение, хранящееся в узле [math]i[/math] и копирует элемент, предыдущий для него.

 pair<T, Stack> pop(i : Node):
   Node k = i.prev
   push(k.prev, k.value)
   return pair(i.value, s)

Пример

Пусть изначально у нас есть один пустой стек. Запишем его в массив.

index	1
value	[math]\mathtt{null}[/math]
prev	[math]\mathtt{null}[/math]

Далее выполним [math]\mathrm{push}(1, 3)[/math]. Создается новая вершина со значением [math]3[/math], ссылающаяся на 1-ую, помещаем ее во 2-ую ячейку массива:

index	1	2
value	[math]\mathtt{null}[/math]	3
prev	[math]\mathtt{null}[/math]	1

Аналогично выполним [math]\mathrm{push}(2, 5)[/math]:

index	1	2	3
value	[math]\mathtt{null}[/math]	3	5
prev	[math]\mathtt{null}[/math]	1	2

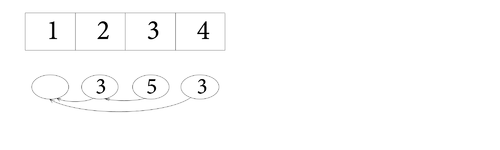
Выполним [math]\mathrm{pop}(3)[/math]. он возвращает [math]5[/math] и копирует 2-ую вершину.

index	1	2	3	4
value	[math]\mathtt{null}[/math]	3	5	3
prev	[math]\mathtt{null}[/math]	1	2	1

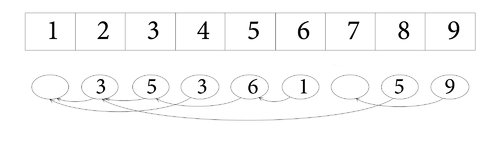
Так будет выглядеть массив после последовательности операций [math]\mathrm{push}(3, 6), \mathrm{push}(5, 1), \mathrm{pop}(4), \mathrm{pop}(5), \mathrm{push}(7, 9):[/math]

index	1	2	3	4	5	6	7	8	9
value	[math]\mathtt{null}[/math]	3	5	3	6	1	[math]\mathtt{null}[/math]	5	9
prev	[math]\mathtt{null}[/math]	1	2	1	3	5	[math]\mathtt{null}[/math]	2	7

В итоге мы имеем доступ ко всем версиям стека за [math]O(1)[/math] времени и [math]O(n)[/math] памяти.

Пример задачи

N детей по очереди лепят снеговиков. Первый ребенок слепил снеговик из одного шара радиусом R1. Каждый следующий ребенок слепил такого же снеговика, как и предыдущий, но подумав немного либо добавил шар радиусом Ri, либо разрушил верхний, уже имеющийся шар. Гарантируется, что все снеговики имеют строго положительное число шаров. Входные данные — N, информация о каждом из детей о том, разрушил ли он последний шар, либо добавил свой (тогда дается и его радиус). Далее дается набор из K чисел в пределах от 1-го до N, для каждого требуется вывести последовательность шаров в снеговике с таким номером. Ограничение на N и K — миллион.

См. также

• Стек
• Персистентный дек

Источники информации

• Habrahabr — Персистентный стек