PpmtnriLmax — различия между версиями
| Строка 8: | Строка 8: | ||
</ol> | </ol> | ||
| − | Необходимо составить такое расписание, чтобы значение <tex>L_{max} = | + | Необходимо составить такое расписание, чтобы значение <tex>L_{max} = \max\limits_{i=1..n} (C_i - d_i)</tex> было минимальным.}} |
== Решение == | == Решение == | ||
| Строка 32: | Строка 32: | ||
Т.к. сеть содержит <tex>O(N)</tex> элементов, значит максимальный поток в ней можно найти за <tex>O(n^3)</tex>. Кроме того, построение "окон" выполнения работ займет <tex>O(N^2)</tex>. Т.о. указанный выше алгоритм потребует <tex>O(N^3)</tex> операций. | Т.к. сеть содержит <tex>O(N)</tex> элементов, значит максимальный поток в ней можно найти за <tex>O(n^3)</tex>. Кроме того, построение "окон" выполнения работ займет <tex>O(N^2)</tex>. Т.о. указанный выше алгоритм потребует <tex>O(N^3)</tex> операций. | ||
| − | Для решения данной задачи мы используем бинпоиск по <tex>L</tex> значениям, а значит, получаем алгоритм с <tex>\varepsilon</tex>-приближенной сложностью <tex>O (n^3(log(n) + log(1 / \varepsilon) + log(\max\limits_{j=1..n} p_j)) </tex>, потому как <tex>L_{max}</tex>, ограничен <tex>n \max\limits_{j=1..n}p_j</tex> | + | Для решения данной задачи мы используем бинпоиск по <tex>L</tex> значениям, а значит, получаем алгоритм с <tex>\varepsilon</tex>-приближенной сложностью <tex>O (n^3(log(n) + log(1 / \varepsilon) + log(\max\limits_{j=1..n} (p_j))) </tex>, потому как <tex>L_{max}</tex>, ограничен <tex>n\max\limits_{j=1..n} (p_j)</tex> |
[[Категория: Дискретная математика и алгоритмы]] | [[Категория: Дискретная математика и алгоритмы]] | ||
[[Категория: Теория расписаний]] | [[Категория: Теория расписаний]] | ||
Версия 18:40, 13 июня 2015
| Задача: |
|
Решение
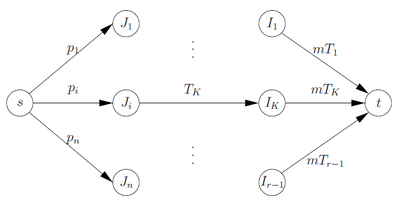
Сведем эту задачу к поиску максимального потока в сети, построенной указанным ниже образом.
Пусть - упорядоченная последовательность и . Определим интервалы с длиной для всех .
Работам сопоставим свой тип вершин, а интервалам свой. Добавим две фиктивные вершины и . Вершина соединена с вершинами ребрами с пропускной способностью , вершина соединена с вершинами ребрами с пропускной способностью . Ребро между вершиной и вершиной существует, если . Пропускная способность этого ребра - .
Нетрудно понять, что расписание существует, если максимальный поток через эту сеть равен .
Если это так, то поток на дуге соответствует тому, что работа будет выполняться во временном интервале , и будет справедливо следующее:
- для всех ребер
Исходя из этого, расписание строится выполнением работы с временем выполнения в интервале .
Т.к. сеть содержит элементов, значит максимальный поток в ней можно найти за . Кроме того, построение "окон" выполнения работ займет . Т.о. указанный выше алгоритм потребует операций.
Для решения данной задачи мы используем бинпоиск по значениям, а значит, получаем алгоритм с -приближенной сложностью , потому как , ограничен