Эвристики для поиска кратчайших путей — различия между версиями
Zemskovk (обсуждение | вклад) м (→Ссылки) |
Zemskovk (обсуждение | вклад) м (Тире) |
||
| Строка 4: | Строка 4: | ||
* <tex>l(u,v) \geqslant 0</tex> | * <tex>l(u,v) \geqslant 0</tex> | ||
* <tex>|V|=n, |E|=m</tex> | * <tex>|V|=n, |E|=m</tex> | ||
| − | * отправная точка | + | * отправная точка — вершина <tex>s</tex>, пункт назначения — вершина <tex>t</tex> |
Цель: найти кратчайший путь <tex> s \rightsquigarrow t</tex> | Цель: найти кратчайший путь <tex> s \rightsquigarrow t</tex> | ||
Мы будем рассматривать сеть автомобильных дорог: | Мы будем рассматривать сеть автомобильных дорог: | ||
| − | * <tex>V</tex> | + | * <tex>V</tex> — множество перекрёстков |
| − | * <tex>E</tex> | + | * <tex>E</tex> — множество дорог |
| − | * <tex>l(u,v)</tex> | + | * <tex>l(u,v)</tex> — среднее время, которое занимает проезд по дороге |
==Алгоритм Дейкстры== | ==Алгоритм Дейкстры== | ||
| Строка 51: | Строка 51: | ||
* При релаксации будем убирать вершину из исходной корзины и класть в корзину, соответствующую новому значению <tex>d(u)</tex> | * При релаксации будем убирать вершину из исходной корзины и класть в корзину, соответствующую новому значению <tex>d(u)</tex> | ||
| − | Можно заметить, что при такой реализации, все операции с приоритетной очередью будут выполняться за <tex>O(1)</tex>. Тогда, для одноуровневой реализации время работы алгоритма Дейкстры можно оценить как <tex>O(m+nC)</tex>, где <tex>C</tex> | + | Можно заметить, что при такой реализации, все операции с приоритетной очередью будут выполняться за <tex>O(1)</tex>. Тогда, для одноуровневой реализации время работы алгоритма Дейкстры можно оценить как <tex>O(m+nC)</tex>, где <tex>C</tex> — максимальная длина ребра в графе. |
При двухуровневой реализации будем поддерживать два уровня корзин: первый уровень будет соответствовать одноуровневой реализации, а корзины второго уровня будут содержать диапазон значений корзин первого уровня, которые в них входят. В этом случае, нам нужно поддерживать два индекса <tex>L_{top}</tex> и <tex>L_{bottom}</tex> для каждого из уровней соответственно. | При двухуровневой реализации будем поддерживать два уровня корзин: первый уровень будет соответствовать одноуровневой реализации, а корзины второго уровня будут содержать диапазон значений корзин первого уровня, которые в них входят. В этом случае, нам нужно поддерживать два индекса <tex>L_{top}</tex> и <tex>L_{bottom}</tex> для каждого из уровней соответственно. | ||
| Строка 58: | Строка 58: | ||
====Калибровка (caliber)==== | ====Калибровка (caliber)==== | ||
| − | Введём величину <b><i>калибр (caliber)</i></b> вершины <tex>c(v)</tex> | + | Введём величину <b><i>калибр (caliber)</i></b> вершины <tex>c(v)</tex> — вес минимального ребра, входящего в <tex>v</tex> , или <tex>\infty</tex>, если в вершину не входит ни одно ребро. Будем говорить, что текущее значение <tex>d(v)</tex> точно, если оно равно длине пути <tex>s \rightsquigarrow v</tex>. |
{{Лемма | {{Лемма | ||
|about = 1 | |about = 1 | ||
|statement = | |statement = | ||
| − | Предположим, что длины рёбер неотрицательны. Пусть <tex>\mu</tex> | + | Предположим, что длины рёбер неотрицательны. Пусть <tex>\mu</tex> — минимальное из текущих значений <tex>d(v):v \in V</tex>. Тогда, если существует такая вершина <tex>u</tex>, что <tex>\mu + c(u) \geqslant d(u)</tex>, то текущее значение <tex>d(u)</tex> точно. |
}} | }} | ||
Эта лемма позволяет нам смягчить правило выбора текущей вершины в алгоритме Дейкстры, при этом сохраняя инвариант (почти все вершины обрабатываются единожды). | Эта лемма позволяет нам смягчить правило выбора текущей вершины в алгоритме Дейкстры, при этом сохраняя инвариант (почти все вершины обрабатываются единожды). | ||
Калибровка использует Лемму 1 чтобы находить и обрабатывать вершины с точными текущими значениями расстояния до них. | Калибровка использует Лемму 1 чтобы находить и обрабатывать вершины с точными текущими значениями расстояния до них. | ||
| − | Модифицируем нашу MLB | + | Модифицируем нашу MLB — структуру: будем хранить помеченные вершины в двух структурах: дерево поиска <tex>F</tex> и приоритетная очередь <tex>B</tex>, реализованная на MLB. |
Алгоритм, приведённый ниже, называется <b><i>алгоритмом умной очереди (smart queue)</i></b>. | Алгоритм, приведённый ниже, называется <b><i>алгоритмом умной очереди (smart queue)</i></b>. | ||
| Строка 73: | Строка 73: | ||
<tex>B</tex> вершину с минимальной меткой и прорелаксируем всех её соседей. | <tex>B</tex> вершину с минимальной меткой и прорелаксируем всех её соседей. | ||
| − | Рассмотрим механизм релаксации: пусть мы уменьшаем <tex>d(u)</tex>. Заметим, что в этом случае <tex>u</tex> не могло лежать в <tex>F</tex> (иначе <tex>d(u)</tex> было не точно). Если <tex>u \in B</tex> | + | Рассмотрим механизм релаксации: пусть мы уменьшаем <tex>d(u)</tex>. Заметим, что в этом случае <tex>u</tex> не могло лежать в <tex>F</tex> (иначе <tex>d(u)</tex> было не точно). Если <tex>u \in B</tex> — применим <tex>\mathtt{decrease — key}</tex> к <tex>u</tex>. Эта операция либо переместила <tex>u</tex> внутри <tex>B</tex>, либо определила, что метка <tex>d(u)</tex> точна и переместила <tex>u</tex> в <tex>F</tex>. |
Если же <tex>u \notin F </tex> и <tex>u \notin B</tex>, мы применим операцию <tex>\mathtt{insert}</tex>, и <tex>u</tex> запишется в | Если же <tex>u \notin F </tex> и <tex>u \notin B</tex>, мы применим операцию <tex>\mathtt{insert}</tex>, и <tex>u</tex> запишется в | ||
<tex>F</tex> или <tex>B</tex>, в зависимости от того, выполняется ли условие леммы. | <tex>F</tex> или <tex>B</tex>, в зависимости от того, выполняется ли условие леммы. | ||
| Строка 80: | Строка 80: | ||
Мы можем уменьшить количество посещённых вершин в алгоритме Дейкстры, просто запустив его и из начальной и из конечной вершины. Такая эвристика не испортит скорость работы в худшем случае. | Мы можем уменьшить количество посещённых вершин в алгоритме Дейкстры, просто запустив его и из начальной и из конечной вершины. Такая эвристика не испортит скорость работы в худшем случае. | ||
| − | Создадим две приоритетных очереди и запустим на одной из них алгоритм Дейкстры, ищущий <tex>d_{forward}(v)</tex> из <tex>s</tex>, а на другой | + | Создадим две приоритетных очереди и запустим на одной из них алгоритм Дейкстры, ищущий <tex>d_{forward}(v)</tex> из <tex>s</tex>, а на другой — ищущий <tex>d_{reverse}(v)</tex> из <tex>t</tex>. Алгоритм завершит свою работу, когда какая-нибудь вершина <tex>z</tex> будет удалена из обоих очередей. |
Тонкость этого алгоритма заключается в том, что кратчайший путь <tex>s \rightsquigarrow t</tex> не обязательно пройдёт через вершину <tex>z</tex>. Поэтому после остановки двунаправленного поиска, нам необходимо перебрать все рёбра из вершин, имеющих <tex>d_{forward}(u)</tex> в | Тонкость этого алгоритма заключается в том, что кратчайший путь <tex>s \rightsquigarrow t</tex> не обязательно пройдёт через вершину <tex>z</tex>. Поэтому после остановки двунаправленного поиска, нам необходимо перебрать все рёбра из вершин, имеющих <tex>d_{forward}(u)</tex> в | ||
| − | вершины с <tex>d_{reverse}(v)</tex> и найти ребро <tex>uv</tex> с минимальным <tex>d_{forward}(u)+\ell(uv)+ d_{reverse}(v) </tex>. Если эта величина меньше, чем длина первоначально найденного пути | + | вершины с <tex>d_{reverse}(v)</tex> и найти ребро <tex>uv</tex> с минимальным <tex>d_{forward}(u)+\ell(uv)+ d_{reverse}(v) </tex>. Если эта величина меньше, чем длина первоначально найденного пути — то это и есть результат работы алгоритма. |
На практике, такой двунаправленный поиск быстрее обычного алгоритма Дейкстры примерно в два раза. | На практике, такой двунаправленный поиск быстрее обычного алгоритма Дейкстры примерно в два раза. | ||
| Строка 92: | Строка 92: | ||
Приведём немного изменённую версию этого алгоритма. | Приведём немного изменённую версию этого алгоритма. | ||
| − | Возьмём функцию <tex>h(v): V \rightarrow \mathbb{R} </tex> | + | Возьмём функцию <tex>h(v): V \rightarrow \mathbb{R} </tex> — <b><i>потенциал (potential)</i></b> вершины. Тогда, с её помощью можно определить <b><i>потенциальную стоимость (reduced cost)</i></b> каждого ребра как <tex>\ell_{h}(v,w) = \ell(v,w)-h(v)+h(w)</tex> |
Заметим, что замена <tex>\ell</tex> на <tex>\ell_{h}</tex> не изменит кратчайших путей: возьмём любой путь <tex>P = (s=v_{0},v_{1},...,v_{k},v_{k+1}=t)</tex>. Тогда <tex>\ell_{h}(P) = \ell_{h}(s,v_{1}), \ell_{h}(s,v_{w})</tex>. Тогда <tex>\ell_{h}(P) = \ell_{h}(s,v_{1})+\ell_{h}(v_{1},v_{2})+...+\ell_{h}(v_{k},t) =</tex> <tex> \ell(s,v_{1})-h(s)+h(v_{1})+\ell(v_{1},v_{2})-h(v_1)+h(v_{2})+...+\ell(v_{k},t)-h(v_k)+h(t) = </tex> <tex>\ell(P)-h(s)+h(t)</tex>. | Заметим, что замена <tex>\ell</tex> на <tex>\ell_{h}</tex> не изменит кратчайших путей: возьмём любой путь <tex>P = (s=v_{0},v_{1},...,v_{k},v_{k+1}=t)</tex>. Тогда <tex>\ell_{h}(P) = \ell_{h}(s,v_{1}), \ell_{h}(s,v_{w})</tex>. Тогда <tex>\ell_{h}(P) = \ell_{h}(s,v_{1})+\ell_{h}(v_{1},v_{2})+...+\ell_{h}(v_{k},t) =</tex> <tex> \ell(s,v_{1})-h(s)+h(v_{1})+\ell(v_{1},v_{2})-h(v_1)+h(v_{2})+...+\ell(v_{k},t)-h(v_k)+h(t) = </tex> <tex>\ell(P)-h(s)+h(t)</tex>. | ||
| Строка 100: | Строка 100: | ||
В нашем случае, алгоритм A* будет эквивалентен алгоритму Дейкстры, на графе <tex>G_{h}</tex>, у которого стоимости рёбер заменили на их потенциальные стоимости. На каждом шаге необходимо будет выбирать из очереди вершину <tex>v</tex> с минимальным значением <tex>\ell(P_{s \rightsquigarrow v})-h(s)+h(v)</tex>. Очевидно, <tex>h(s)</tex> будет одинаковым для любой вершины <tex>v</tex>. | В нашем случае, алгоритм A* будет эквивалентен алгоритму Дейкстры, на графе <tex>G_{h}</tex>, у которого стоимости рёбер заменили на их потенциальные стоимости. На каждом шаге необходимо будет выбирать из очереди вершину <tex>v</tex> с минимальным значением <tex>\ell(P_{s \rightsquigarrow v})-h(s)+h(v)</tex>. Очевидно, <tex>h(s)</tex> будет одинаковым для любой вершины <tex>v</tex>. | ||
| − | Назовём функцию <tex>h</tex> <b>правдоподобной (<i>feasible</i>)</b>, если <tex>\forall (u,v): \ell_{h}(u,v) \geqslant 0</tex>. Известно, что, если <tex>h(t)\leqslant 0</tex> и <tex>h</tex> правдоподобна, то для любого <tex>v</tex>, <tex>h(v)</tex> | + | Назовём функцию <tex>h</tex> <b>правдоподобной (<i>feasible</i>)</b>, если <tex>\forall (u,v): \ell_{h}(u,v) \geqslant 0</tex>. Известно, что, если <tex>h(t)\leqslant 0</tex> и <tex>h</tex> правдоподобна, то для любого <tex>v</tex>, <tex>h(v)</tex> — нижняя граница <tex>d(v,t)</tex> |
| − | Главное отличие от алгоритма Дейкстры в том, что A* является <b>информированным</b> алгоритмом | + | Главное отличие от алгоритма Дейкстры в том, что A* является <b>информированным</b> алгоритмом — он обрабатывает в первую очередь те вершины, которые находятся ближе к результату. |
Скорость работы алгоритма A*: | Скорость работы алгоритма A*: | ||
| − | * в худшем случае | + | * в худшем случае — <tex>h(v)=0</tex> - вырождается в алгоритм Дейкстры |
| − | * в лучшем случае | + | * в лучшем случае — <tex>\forall v: h(v)=d(v,t)</tex> |
**<tex>\ell_{h}(v,w)=0</tex>, если ребро <tex>(v,w)</tex> лежит на кратчайшем пути, иначе потенциальная стоимость положительна | **<tex>\ell_{h}(v,w)=0</tex>, если ребро <tex>(v,w)</tex> лежит на кратчайшем пути, иначе потенциальная стоимость положительна | ||
**все посещённые вершины будут лежать на кратчайшем пути | **все посещённые вершины будут лежать на кратчайшем пути | ||
| Строка 116: | Строка 116: | ||
В этом случае появляется дополнительная проблема: различные потенциальные стоимости у рёбер для различных обходов: | В этом случае появляется дополнительная проблема: различные потенциальные стоимости у рёбер для различных обходов: | ||
| − | *<tex>\ell_{p_{f}}(v,w) = \ell(v,w)-p_{f}(v)+p_{f}(w)</tex> | + | *<tex>\ell_{p_{f}}(v,w) = \ell(v,w)-p_{f}(v)+p_{f}(w)</tex> — если ребро обрабатывается в обходе, начатом в <tex>s</tex> |
| − | *<tex>\ell_{p_{r}}(v,w) = \ell(v,w)-p_{r}(w)+p_{r}(v)</tex> | + | *<tex>\ell_{p_{r}}(v,w) = \ell(v,w)-p_{r}(w)+p_{r}(v)</tex> — если ребро обрабатывается в обходе, начатом в <tex>t</tex> |
Чтобы избежать этой проблемы, необходимо, чтобы <tex>\ell_{p_{f}}(v,w) = \ell_{p_{r}}(v,w) \Leftrightarrow p_{f}(v) + p_{r}(v) = p_{f}(w) + p_{r}(w) = const</tex>. Кроме того, функции должны бить монотонными. | Чтобы избежать этой проблемы, необходимо, чтобы <tex>\ell_{p_{f}}(v,w) = \ell_{p_{r}}(v,w) \Leftrightarrow p_{f}(v) + p_{r}(v) = p_{f}(w) + p_{r}(w) = const</tex>. Кроме того, функции должны бить монотонными. | ||
| − | Решение | + | Решение — использовать усреднённые потенциальные функции: |
*<tex>h_{f}(v) = \frac{p_{f}(v)-p_{r}(v)}{2}</tex> | *<tex>h_{f}(v) = \frac{p_{f}(v)-p_{r}(v)}{2}</tex> | ||
*<tex>h_{r}(v) = \frac{p_{r}(v)-p_{f}(v)}{2} = -h_{f}(v)</tex> | *<tex>h_{r}(v) = \frac{p_{r}(v)-p_{f}(v)}{2} = -h_{f}(v)</tex> | ||
| Строка 140: | Строка 140: | ||
Можно рассмотреть в этом ключе два примера: | Можно рассмотреть в этом ключе два примера: | ||
| − | * Алгоритм Дейкстры: препроцессинг | + | * Алгоритм Дейкстры: препроцессинг — ничего не делать, запрос — выполнение алгоритма Дейкстры; |
| − | * Полный перебор: препроцессинг | + | * Полный перебор: препроцессинг — посчитать таблицу расстояний размером <tex>n \times n</tex> (займёт порядка 5 лет времени и 1 петабайта памяти для карты Европы), запрос — обратиться к элементу таблицы. |
| − | Оба эти примера | + | Оба эти примера — крайние случаи. Нам нужно нечто более гибкое: препроцессинг за часы/минуты, рост количества предпосчитанных данных линейно от размера графа и запросы в реальном времени. |
===ALT=== | ===ALT=== | ||
| Строка 156: | Строка 156: | ||
Запрос: | Запрос: | ||
* используем A* | * используем A* | ||
| − | * если некоторое ребро находится на кратчайшем пути между исходной точкой и ориентиром | + | * если некоторое ребро находится на кратчайшем пути между исходной точкой и ориентиром — по нему идём в первую очередь |
[[Файл:ALT.jpg|right|frame|рис. 1]] | [[Файл:ALT.jpg|right|frame|рис. 1]] | ||
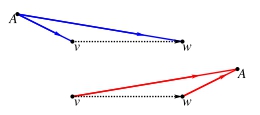
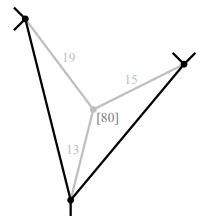
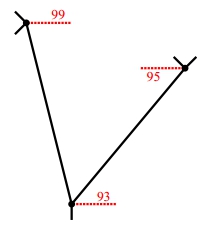
| − | Будем использовать неравенство треугольника для нижних оценок пути (см. рис. 1). Пусть <tex>A</tex> | + | Будем использовать неравенство треугольника для нижних оценок пути (см. рис. 1). Пусть <tex>A</tex> — один из ориентиров, тогда: |
*<tex>dist(v,w)\ge dist(A,w)-dist(A,v)</tex> | *<tex>dist(v,w)\ge dist(A,w)-dist(A,v)</tex> | ||
*<tex>dist(v,w)\ge dist(v,A)-dist(w,A)</tex> | *<tex>dist(v,w)\ge dist(v,A)-dist(w,A)</tex> | ||
| Строка 204: | Строка 204: | ||
Эта эвристика основывается на интуитивном наблюдении: не стоит посещать "локальные" дороги, когда мы находимся достаточно далеко и от <tex>s</tex>, и от <tex>t</tex> | Эта эвристика основывается на интуитивном наблюдении: не стоит посещать "локальные" дороги, когда мы находимся достаточно далеко и от <tex>s</tex>, и от <tex>t</tex> | ||
| − | Пусть вершина <tex>v</tex> лежит на кратчайшем пути <tex>P: s \rightsquigarrow t</tex>. Тогда, назовём <b>охватом (reach)</b> вершины <tex>v</tex> относительно <tex>P</tex> величину <tex>r(v,P) = \min\{dist(s,v), dist(v,t)\}</tex>. Охватом вершины относительно всего графа назовём величину <tex>r(v) = \max\limits_{P} r(v,P)</tex> | + | Пусть вершина <tex>v</tex> лежит на кратчайшем пути <tex>P: s \rightsquigarrow t</tex>. Тогда, назовём <b>охватом (reach)</b> вершины <tex>v</tex> относительно <tex>P</tex> величину <tex>r(v,P) = \min\{dist(s,v), dist(v,t)\}</tex>. Охватом вершины относительно всего графа назовём величину <tex>r(v) = \max\limits_{P} r(v,P)</tex> — максимум по всем кратчайшим путям, содержащим <tex>v</tex>. |
| − | Помимо этого, будет полезным ввести понятие охвата ребра. Назовём охватом ребра <tex>(v,w)\in P</tex> относительно <tex>P</tex> величину <tex>\min\{dist(s,v), dist(w,t)\}</tex>. Аналогично, охватом ребра относительно всего графа назовём величину <tex>r(v,w) = \max\limits_{P} r((v,w),P)</tex> | + | Помимо этого, будет полезным ввести понятие охвата ребра. Назовём охватом ребра <tex>(v,w)\in P</tex> относительно <tex>P</tex> величину <tex>\min\{dist(s,v), dist(w,t)\}</tex>. Аналогично, охватом ребра относительно всего графа назовём величину <tex>r(v,w) = \max\limits_{P} r((v,w),P)</tex> — максимум по всем кратчайшим путям, содержащим <tex>(v,w)</tex>. |
[[Файл:reach1.jpg|right]] | [[Файл:reach1.jpg|right]] | ||
| Строка 233: | Строка 233: | ||
* для каждой вершины <tex>s \in V</tex> рассмотрим дерево кратчайших путей до всех других вершин <tex>T_{s}</tex>. | * для каждой вершины <tex>s \in V</tex> рассмотрим дерево кратчайших путей до всех других вершин <tex>T_{s}</tex>. | ||
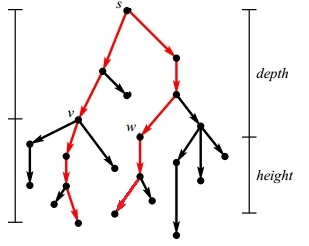
**найдём наиболее длинный путь <tex>P_{s\rightsquigarrow t}</tex>, содержащий <tex>v</tex>. | **найдём наиболее длинный путь <tex>P_{s\rightsquigarrow t}</tex>, содержащий <tex>v</tex>. | ||
| − | **Назовём глубиной вершины <tex>d_{s}(v)</tex> расстояние от <tex>s</tex>, высотой вершины <tex>h_{s}(v)</tex> | + | **Назовём глубиной вершины <tex>d_{s}(v)</tex> расстояние от <tex>s</tex>, высотой вершины <tex>h_{s}(v)</tex> — расстояние до наиболее далёкого потомка вершины |
** Тогда, охватом вершины в этом дереве будет величина <tex>r_{s}(v) = \min\{d_{s}(v),h_{s}(v)\}</tex> | ** Тогда, охватом вершины в этом дереве будет величина <tex>r_{s}(v) = \min\{d_{s}(v),h_{s}(v)\}</tex> | ||
** Тогда обновим значение охвата <tex>r(v) \leftarrow \max\{r(v),r_{s}(v)\}</tex> | ** Тогда обновим значение охвата <tex>r(v) \leftarrow \max\{r(v),r_{s}(v)\}</tex> | ||
| Строка 241: | Строка 241: | ||
Финальная версия препроцессинга будет иметь две фазы: | Финальная версия препроцессинга будет иметь две фазы: | ||
*основная фаза (строятся частично обработанные деревья и добавляются сокращающие путь рёбра) | *основная фаза (строятся частично обработанные деревья и добавляются сокращающие путь рёбра) | ||
| − | *фаза отладки (вершины с большим охватом обрабатываются указанным выше алгоритмом | + | *фаза отладки (вершины с большим охватом обрабатываются указанным выше алгоритмом — их гораздо меньше, поэтому обработка будет быстрой) |
====Сокращение области поиска==== | ====Сокращение области поиска==== | ||
| Строка 254: | Строка 254: | ||
Таким образом, алгоритм будет выглядеть так: | Таким образом, алгоритм будет выглядеть так: | ||
| − | *найдём оценку охвата <tex>r'(v)</tex>, используя только <tex>\varepsilon</tex> | + | *найдём оценку охвата <tex>r'(v)</tex>, используя только <tex>\varepsilon</tex> — минимальные пути |
* если <tex>r'(v)<\varepsilon</tex>, то оценка корректна: <tex>r(v)=r'(v)</tex> | * если <tex>r'(v)<\varepsilon</tex>, то оценка корректна: <tex>r(v)=r'(v)</tex> | ||
* если же <tex>r'(v)\geq \varepsilon</tex>, то она нас не интересует: <tex>r(v)\geq r'(v)</tex> | * если же <tex>r'(v)\geq \varepsilon</tex>, то она нас не интересует: <tex>r(v)\geq r'(v)</tex> | ||
| − | Полезно будет рассматривать <b>частично обработанные деревья</b> (<i>partial trees</i>) | + | Полезно будет рассматривать <b>частично обработанные деревья</b> (<i>partial trees</i>) — деревья кратчайших путей, хранящие пути длиной, меньшей определённого порога. Тогда дерево кратчайших путей будет глубиной порядка <tex>2\varepsilon</tex>: |
* Установим <tex>G'\leftarrow G</tex> и <tex>\varepsilon\leftarrow \varepsilon_{0}</tex> (маленькое число) | * Установим <tex>G'\leftarrow G</tex> и <tex>\varepsilon\leftarrow \varepsilon_{0}</tex> (маленькое число) | ||
* Пока <tex>G'</tex> не пусто | * Пока <tex>G'</tex> не пусто | ||
| Строка 267: | Строка 267: | ||
[[Файл:reach6.jpg|right]] | [[Файл:reach6.jpg|right]] | ||
====Пенальти==== | ====Пенальти==== | ||
| − | Предыдущее улучшение создаёт проблему: мы должны предполагать, что кратчайший путь может начинаться в вершине с маленьким охватом, которые мы отбрасываем на каждой итерации. Для того, чтобы принять их во внимание, мы введём новую величину | + | Предыдущее улучшение создаёт проблему: мы должны предполагать, что кратчайший путь может начинаться в вершине с маленьким охватом, которые мы отбрасываем на каждой итерации. Для того, чтобы принять их во внимание, мы введём новую величину — <b>пенальти</b>(<i>penalty</i>) — верхнюю оценку на длину кратчайшего пути в "отброшенной" зоне. |
| − | Пусть <tex>G_{i} = (V_{i},A_{i})</tex> | + | Пусть <tex>G_{i} = (V_{i},A_{i})</tex> — подграф исходного графа, полученный на <tex>i</tex>-й итерации алгоритма, описанного выше. Назовём входящим пенальти (<i>in-penalty</i>) вершины <tex>v\in V_{i}</tex> величину <tex>\max\{ \overline{r}(u,v) : u,v \in A \backslash A_{i}\}</tex>, если у <tex>v</tex> было как минимум одно выброшенное в процессе алгоритма входящее ребро, или ноль в противном случае. |
Аналогично определим исходящее пенальти для исходящих из вершины рёбер. | Аналогично определим исходящее пенальти для исходящих из вершины рёбер. | ||
Изменим алгоритм, чтобы заменить вершины на их пенальти. Для этого переопределим глубину и высоту вершины. | Изменим алгоритм, чтобы заменить вершины на их пенальти. Для этого переопределим глубину и высоту вершины. | ||
| − | * Глубиной вершины <tex>v\in T_{x}</tex>, где <tex>T_{x}</tex> | + | * Глубиной вершины <tex>v\in T_{x}</tex>, где <tex>T_{x}</tex> — частично обработанное дерево с корнем в <tex>x</tex> величину <tex>depth(v)=d(v)+in\textrm{-}penalty(x)</tex> , где <tex>d(v)</tex> — длина пути от корня до вершины в дереве. |
| − | * Чтобы определить высоту вершины, нам нужно понятие "ложных листьев". Для каждой вершины <tex>v</tex> в дереве кратчайших путей добавим потомка <tex>v'</tex> | + | * Чтобы определить высоту вершины, нам нужно понятие "ложных листьев". Для каждой вершины <tex>v</tex> в дереве кратчайших путей добавим потомка <tex>v'</tex> — ложный лист, и ребро <tex>(v,v') = out\textrm{-}penalty(v)</tex>. В некотором смысле, <tex>v'</tex> будет выступать в роли всех рёбер, изначально инцидентных вершине <tex>v</tex>, которые мы отсекли. Тогда высотой вершины <tex>v</tex> будет расстояние от неё, до наиболее далёкого ложного листа. Подчеркнём, что в данный момент ложные листья добавляются неявно, и только после того, как дерево будет частично обработано. |
====Сокращение путей==== | ====Сокращение путей==== | ||
| − | Представим последовательность вершин степени 2 с большим охватом, идущих подряд. Добавим, <b>сокращающее ребро</b> (<i>shortcut</i>) | + | Представим последовательность вершин степени 2 с большим охватом, идущих подряд. Добавим, <b>сокращающее ребро</b> (<i>shortcut</i>) — ребро, проходящее из начала пути в его конец с длиной, равной длине этого пути. Таким образом мы можем уменьшить охваты вершин на этом пути и ускорить препроцессинг (уменьшив количество проходимых рёбер), но увеличим память, необходимую для хранения нашего графа. |
На этом шаге мы будем искать <b>пропускаемые</b> (bypassable) вершины. Назовём вершину <tex>v</tex> пропускаемой, если выполняется одно из двух условий: | На этом шаге мы будем искать <b>пропускаемые</b> (bypassable) вершины. Назовём вершину <tex>v</tex> пропускаемой, если выполняется одно из двух условий: | ||
* <tex>v</tex> имеет только одно входящее ребро <tex>(u,v)</tex> и одно исходящее ребро <tex>(v,w)</tex> | * <tex>v</tex> имеет только одно входящее ребро <tex>(u,v)</tex> и одно исходящее ребро <tex>(v,w)</tex> | ||
* <tex>v</tex> имеет два входящих ребра <tex>(u,v)</tex>, <tex>(w,v)</tex> и два исходящих ребра <tex>(v,w)</tex> ,<tex>(v,u)</tex> | * <tex>v</tex> имеет два входящих ребра <tex>(u,v)</tex>, <tex>(w,v)</tex> и два исходящих ребра <tex>(v,w)</tex> ,<tex>(v,u)</tex> | ||
| − | В обоих случаях подразумевается, что <tex>u\neq w</tex>, то есть у <tex>v</tex> обязательно есть только два соседа. В первом случае, <tex>v</tex> | + | В обоих случаях подразумевается, что <tex>u\neq w</tex>, то есть у <tex>v</tex> обязательно есть только два соседа. В первом случае, <tex>v</tex> — кандидат на односторонний пропуск (one-way bypass), во втором — на двухсторонний (two-way bypass). Мы будем использовать сокращающие рёбра, чтобы пропускать такие вершины. |
| − | Линия (line) | + | Линия (line) — путь в графе, содержащий как минимум три вершины, так, что все вершины, кроме начальной и конечной, пропускаемые. Каждая пропускаемая вершина может принадлежать только одной линии. Линии также могут быть односторонне- и двухсторонне- пропускаемыми, в зависимости от типа вершин, которые они содержат. Легко заметить, что на линии могут лежать вершины только одного типа. |
Как только мы нашли линию, самым простым решением будет добавить одно сокращающее ребро из начала в конец. Но практика показывает, что лучше сократить ещё и входящие в её состав линии меньшего размера, это ещё более уменьшит охваты пропускаемых вершин. Для этого перед добавлением сокращающего ребра по линии, рекурсивно найдём вершину, которая находится примерно на её середине и обработаем левый и правый отрезки как полноценные линии. | Как только мы нашли линию, самым простым решением будет добавить одно сокращающее ребро из начала в конец. Но практика показывает, что лучше сократить ещё и входящие в её состав линии меньшего размера, это ещё более уменьшит охваты пропускаемых вершин. Для этого перед добавлением сокращающего ребра по линии, рекурсивно найдём вершину, которая находится примерно на её середине и обработаем левый и правый отрезки как полноценные линии. | ||
| Строка 296: | Строка 296: | ||
====Фаза отладки==== | ====Фаза отладки==== | ||
| − | Тот факт, что мы используем пенальти, для ускорения вычисления корректных верхних оценок охвата, приводит к тому, что оценки становятся менее точными в процессе работы алгоритма и с ростом пенальти. Следовательно, для вершин, которые дольше находятся в графе, ошибки накапливаются. Это плохо, потом что такие вершины и являются самыми важными в графе | + | Тот факт, что мы используем пенальти, для ускорения вычисления корректных верхних оценок охвата, приводит к тому, что оценки становятся менее точными в процессе работы алгоритма и с ростом пенальти. Следовательно, для вершин, которые дольше находятся в графе, ошибки накапливаются. Это плохо, потом что такие вершины и являются самыми важными в графе — у них высокий охват, их посещает большое количество кратчайших путей. Если бы мы могли сделать их более точными, во время запроса можно было бы пропустить большее количество вершин. |
В этом и заключается цель фазы отладки. После того, как мы найдём верные значения верхних оценок, используя частично обработанные деревья, во время фазы отладки мы пересчитаем охват <tex>\delta = const</tex> вершин с наибольшими значениями охвата (в них больше всего ошибок). | В этом и заключается цель фазы отладки. После того, как мы найдём верные значения верхних оценок, используя частично обработанные деревья, во время фазы отладки мы пересчитаем охват <tex>\delta = const</tex> вершин с наибольшими значениями охвата (в них больше всего ошибок). | ||
| − | Пусть <tex>V_{\delta} \subset G</tex> | + | Пусть <tex>V_{\delta} \subset G</tex> — множество вершин с высоким охватом мощностью <tex>\delta</tex>. Чтобы пересчитать их охваты, сначала необходимо найти подграф <tex>G_{\delta} = (V_{\delta},A_{\delta})</tex>. Этот граф содержит не только первоначальные рёбра, но и добавленные во время основной фазы сокращающие рёбра. Затем мы запустим поиск точных значений охвата для каждой вершины этого подграфа. Так как деревья кратчайших путей будут содержать только вершины из <tex>G_{\delta}</tex>, то нам всё ещё нужно использовать входящие и исходящие пенальти для остальных вершин. Но, тем не менее, они будут меньше, т.к. для самых больших мы подсчитали точное значение охвата. |
Во время фазы отладки мы заботимся о точности, а не о скорости, поэтому не добавляем новых сокращающих рёбер и используем точный алгоритм. | Во время фазы отладки мы заботимся о точности, а не о скорости, поэтому не добавляем новых сокращающих рёбер и используем точный алгоритм. | ||
| Строка 327: | Строка 327: | ||
|} | |} | ||
Условные обозначения: | Условные обозначения: | ||
| − | * зелёный квадрат | + | * зелёный квадрат — начало пути |
| − | * синий квадрат | + | * синий квадрат — конец пути |
| − | * зелёные линии | + | * зелёные линии — пути, пройденные прямым обходом |
| − | * синие линии | + | * синие линии — пути, пройденные обратным обходом |
| − | * красные ромбы | + | * красные ромбы — ориентиры |
| − | * жёлтые ромбы | + | * жёлтые ромбы — выбранные при поиске пути ориентиры |
==Источники информации== | ==Источники информации== | ||
Версия 21:33, 27 декабря 2015
Содержание
Проблема поиска кратчайшего пути
Дано:
- ориентированный граф
- отправная точка — вершина , пункт назначения — вершина
Цель: найти кратчайший путь
Мы будем рассматривать сеть автомобильных дорог:
- — множество перекрёстков
- — множество дорог
- — среднее время, которое занимает проезд по дороге
Алгоритм Дейкстры
Основная статья: Алгоритм Дейкстры
- на каждом шаге выбирает из множества непросмотренных вершин вершину с наименьшим расстоянием до старта и релаксирует рёбра, исходящие из неё
- завершает свою работу, когда цель достигнута (или просмотрены все вершины)
Скорость работы алгоритма Дейкстры сильно зависит от скорости операций с приоритетной очередью.
Поскольку мы рассматриваем сеть автомобильных дорог, то (граф планарен почти везде).
Для фибоначчиевых куч время работы алгоритма составляет , для двоичных куч:
Но на практике чаще используются 2-, 4- и 8-ичные кучи: они более простые, оценка времени работы содержит меньшее количество скрытых констант.
Улучшения алгоритма Дейкстры
Многоуровневые корзины (multi-level buckets, MLB)
| Структура данных | Время работы (сек) |
|---|---|
| Двоичная куча | 12,38 |
| 4-куча | 11,53 |
| 8-куча | 11,52 |
| MLB | 9,36 |
| MLB + калибровка | 8,04 |
Подходит только графов с целочисленными рёбрами.
- Будем складывать вершины в "корзины"
- Наша структура данных будет поддерживать индекс
- На каждом шаге алгоритма, если пусто, то увеличим , а иначе достанем одну вершину из
- При релаксации будем убирать вершину из исходной корзины и класть в корзину, соответствующую новому значению
Можно заметить, что при такой реализации, все операции с приоритетной очередью будут выполняться за . Тогда, для одноуровневой реализации время работы алгоритма Дейкстры можно оценить как , где — максимальная длина ребра в графе.
При двухуровневой реализации будем поддерживать два уровня корзин: первый уровень будет соответствовать одноуровневой реализации, а корзины второго уровня будут содержать диапазон значений корзин первого уровня, которые в них входят. В этом случае, нам нужно поддерживать два индекса и для каждого из уровней соответственно.
При такой реализации, время работы алгоритма Дейкстры можно оценить как
Калибровка (caliber)
Введём величину калибр (caliber) вершины — вес минимального ребра, входящего в , или , если в вершину не входит ни одно ребро. Будем говорить, что текущее значение точно, если оно равно длине пути .
| Лемма (1): |
Предположим, что длины рёбер неотрицательны. Пусть — минимальное из текущих значений . Тогда, если существует такая вершина , что , то текущее значение точно. |
Эта лемма позволяет нам смягчить правило выбора текущей вершины в алгоритме Дейкстры, при этом сохраняя инвариант (почти все вершины обрабатываются единожды). Калибровка использует Лемму 1 чтобы находить и обрабатывать вершины с точными текущими значениями расстояния до них.
Модифицируем нашу MLB — структуру: будем хранить помеченные вершины в двух структурах: дерево поиска и приоритетная очередь , реализованная на MLB. Алгоритм, приведённый ниже, называется алгоритмом умной очереди (smart queue).
Вершины в будут иметь точные метки . Если непусто, мы удалим оттуда вершину и прорелаксируем всех её соседей. Если же пусто, мы достанем из вершину с минимальной меткой и прорелаксируем всех её соседей.
Рассмотрим механизм релаксации: пусть мы уменьшаем . Заметим, что в этом случае не могло лежать в (иначе было не точно). Если — применим к . Эта операция либо переместила внутри , либо определила, что метка точна и переместила в . Если же и , мы применим операцию , и запишется в или , в зависимости от того, выполняется ли условие леммы.
Двунаправленный поиск
Мы можем уменьшить количество посещённых вершин в алгоритме Дейкстры, просто запустив его и из начальной и из конечной вершины. Такая эвристика не испортит скорость работы в худшем случае.
Создадим две приоритетных очереди и запустим на одной из них алгоритм Дейкстры, ищущий из , а на другой — ищущий из . Алгоритм завершит свою работу, когда какая-нибудь вершина будет удалена из обоих очередей.
Тонкость этого алгоритма заключается в том, что кратчайший путь не обязательно пройдёт через вершину . Поэтому после остановки двунаправленного поиска, нам необходимо перебрать все рёбра из вершин, имеющих в вершины с и найти ребро с минимальным . Если эта величина меньше, чем длина первоначально найденного пути — то это и есть результат работы алгоритма.
На практике, такой двунаправленный поиск быстрее обычного алгоритма Дейкстры примерно в два раза.
Алгоритм A*
Основная статья: Алгоритм A*
Приведём немного изменённую версию этого алгоритма.
Возьмём функцию — потенциал (potential) вершины. Тогда, с её помощью можно определить потенциальную стоимость (reduced cost) каждого ребра как
Заметим, что замена на не изменит кратчайших путей: возьмём любой путь . Тогда . Тогда .
Таким образом длины все путей изменятся на одну и ту же величину
В нашем случае, алгоритм A* будет эквивалентен алгоритму Дейкстры, на графе , у которого стоимости рёбер заменили на их потенциальные стоимости. На каждом шаге необходимо будет выбирать из очереди вершину с минимальным значением . Очевидно, будет одинаковым для любой вершины .
Назовём функцию правдоподобной (feasible), если . Известно, что, если и правдоподобна, то для любого , — нижняя граница
Главное отличие от алгоритма Дейкстры в том, что A* является информированным алгоритмом — он обрабатывает в первую очередь те вершины, которые находятся ближе к результату.
Скорость работы алгоритма A*:
- в худшем случае — - вырождается в алгоритм Дейкстры
- в лучшем случае —
- , если ребро лежит на кратчайшем пути, иначе потенциальная стоимость положительна
- все посещённые вершины будут лежать на кратчайшем пути
Двунаправленный A*
Для двунаправленной версии алгоритма нам нужны две потенциальные функции:
- , оценивающая
- , оценивающая
В этом случае появляется дополнительная проблема: различные потенциальные стоимости у рёбер для различных обходов:
- — если ребро обрабатывается в обходе, начатом в
- — если ребро обрабатывается в обходе, начатом в
Чтобы избежать этой проблемы, необходимо, чтобы . Кроме того, функции должны бить монотонными.
Решение — использовать усреднённые потенциальные функции:
При таком выборе потенциальных функций, выполняется и тогда двунаправленный A* становится аналогичен двунаправленному алгоритму Дейкстры
Двухэтапные алгоритмы
К сожалению, двунаправленный алгоритм Дейкстры всего в два раза быстрее обычного, а это слишком медленно. Рассмотрим алгоритм поиска кратчайшего пути, состоящий из двух этапов:
- Препроцессинг
- запускается единожды для графа
- может занимать много времени
- рассчитывает некую вспомогательную информацию
- Запрос
- может использовать данные, полученные во время препроцессинга
- запускается по требованию для пары
- должен выполняться очень быстро (в реальном времени)
Можно рассмотреть в этом ключе два примера:
- Алгоритм Дейкстры: препроцессинг — ничего не делать, запрос — выполнение алгоритма Дейкстры;
- Полный перебор: препроцессинг — посчитать таблицу расстояний размером (займёт порядка 5 лет времени и 1 петабайта памяти для карты Европы), запрос — обратиться к элементу таблицы.
Оба эти примера — крайние случаи. Нам нужно нечто более гибкое: препроцессинг за часы/минуты, рост количества предпосчитанных данных линейно от размера графа и запросы в реальном времени.
ALT
Аббревиатура ALT расшифровывается как A* +Landmarks + Triangle inequality : A* + ориентиры + неравенство треугольника.
Препроцессинг:
- взять небольшое количество вершин (например, 16), обозначив их как ориентиры (landmarks)
- для каждого из ориентиров посчитать кратчайшие пути до всех вершин
- сохранить эти пути
Запрос:
- используем A*
- если некоторое ребро находится на кратчайшем пути между исходной точкой и ориентиром — по нему идём в первую очередь
Будем использовать неравенство треугольника для нижних оценок пути (см. рис. 1). Пусть — один из ориентиров, тогда:
Эта эвристика хорошо работает, на дорожных графах, для которых верно следующее: как правило, кратчайший путь затрагивает небольшое количество локальных дорог, потом крупную автомагистраль и снова некоторое количество локальных дорог.
Сложности в выборе ориентиров:
- хороший ориентир для запроса должен находиться "до" (точно не будет общих рёбер на кратчайшем пути) или "за" (чем острее угол, тем меньше отклонение от предварительно посчитанного кратчайшего пути до искомого)
- Нам нужно выбрать такие ориентиры, которые будут неплохими для всех запросов.
Выглядит логичным выбирать ориентиры на краю дорожной сети, тогда будет больше острых углов и ориентиры будут лучше.
Существуют различные алгоритмы выбора ориентиров:
Случайный выбор (random)
Как следует из названия, ориентиры выбираются случайным образом
Плоскостной (planar)
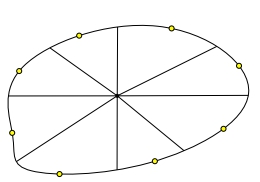
- разделим карту на секторов одинаковой площади
- возьмём ориентиром наиболее удалённую точку от центра в каждом секторе
Такой способ подходит, только если граф имеет относительно правильную форму. На практике обычно используется оптимизированная версия этого алгоритма.
Избирательный (avoid)
Этот алгоритм добавляет ориентиры по одному, глядя на вершины, которые плохо покрыты текущим набором ориентиров .
Построим из случайно выбранной вершины дерево кратчайших путей . Весом каждой вершины в этом дереве назовём разность между истинной длиной пути и нижней оценкой этой длины , полученной по текущему набору ориентиров. Размером вершины назовём сумму её веса и размеров всех её потомков в . Если поддерево с корнем в содержит ориентир, размер равен 0.
Начиная с максимальной по размеру вершины, пойдём вниз по дереву и найдём лист с максимальным размером. Примем его за новый ориентир.
Поиск максимального покрытия (maxCover)
Основным минусом избирательного метода является то, что первый ориентир выбирается случайным образом и выбор последующих ориентиров будет сильно зависеть от первоначального.
Мы можем улучшить найденные ориентиры, если сначала, используя избирательный метод, найдём набор ориентиров в несколько (обычно, 4) раза больше, чем необходимо, а потом отсеем лишние минимизируя время запроса.
Оценим качество набора ориентиров основываясь на покрытии дуг. Будем говорить, что ориентир покрывает дугу , если вершина находится на кратчайшем пути . То есть, , тогда такой выбор ориентира даст нам нижнюю границу для всех путей, содержащих .
Если хотя бы один ориентир из покрывает дугу , то и весь покрывает эту дугу.
Этот метод является наилучшим, но является наиболее медленным. Задача выбора ориентиров в этом случае становится NP-полной.
Reach
Эта эвристика основывается на интуитивном наблюдении: не стоит посещать "локальные" дороги, когда мы находимся достаточно далеко и от , и от
Пусть вершина лежит на кратчайшем пути . Тогда, назовём охватом (reach) вершины относительно величину . Охватом вершины относительно всего графа назовём величину — максимум по всем кратчайшим путям, содержащим .
Помимо этого, будет полезным ввести понятие охвата ребра. Назовём охватом ребра относительно величину . Аналогично, охватом ребра относительно всего графа назовём величину — максимум по всем кратчайшим путям, содержащим .
Заметим, что вершины с большим охватом находятся вблизи середины некоторого длинного кратчайшего пути, то есть
- на больших автомагистралях вершины имеют большой охват
- на локальных перекрёстках (внутри населённых пунктов) вершины имеют маленький охват
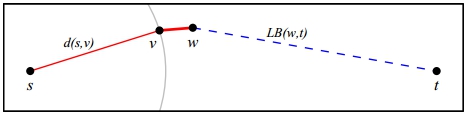
Во время обработки ребра :
- удалим вершину , если
- оценка должна быть подобрана таким образом, чтобы, если бы было кратчайшим путём, было бы больше.
Как искать нижнюю оценку длины пути ?
- Явно: Евклидово расстояние, с помощью ориентиров
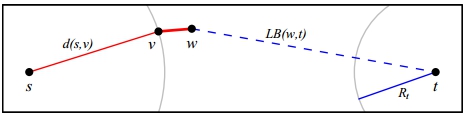
- Неявно: сделать поиск двунаправленным
Например, радиус поиска в обратную сторону может быть нижней оценкой, т.к. если вершина не была посещена поиском в обратную сторону, то
Таким образом, будем удалять , если
Для улучшения результата, нам необходимо сбалансировать прямой и обратный поиск.
Рассмотрим препроцессинг:
- на начальном этапе
- для каждой вершины рассмотрим дерево кратчайших путей до всех других вершин .
- найдём наиболее длинный путь , содержащий .
- Назовём глубиной вершины расстояние от , высотой вершины — расстояние до наиболее далёкого потомка вершины
- Тогда, охватом вершины в этом дереве будет величина
- Тогда обновим значение охвата
Сложность алгоритма: , поэтому он слишком медленный для больших графов и его нужно улучшить.
Финальная версия препроцессинга будет иметь две фазы:
- основная фаза (строятся частично обработанные деревья и добавляются сокращающие путь рёбра)
- фаза отладки (вершины с большим охватом обрабатываются указанным выше алгоритмом — их гораздо меньше, поэтому обработка будет быстрой)
Сокращение области поиска
Заметим, что нам нужны только вершины с маленьким охватом . Заметим также, что если , то существует такой путь , что на нем лежит вершина , для которой выполняется условие
Назовём кратчайший путь -минимальным, если выполняются условия
Таким образом, алгоритм будет выглядеть так:
- найдём оценку охвата , используя только — минимальные пути
- если , то оценка корректна:
- если же , то она нас не интересует:
Полезно будет рассматривать частично обработанные деревья (partial trees) — деревья кратчайших путей, хранящие пути длиной, меньшей определённого порога. Тогда дерево кратчайших путей будет глубиной порядка :
- Установим и (маленькое число)
- Пока не пусто
- найдём частично обработанное дерево кратчайших путей из , чтобы найти вершины с охватом
- удалим из оставшиеся вершины (с охватом , уже обработанные)
- установим
Пенальти
Предыдущее улучшение создаёт проблему: мы должны предполагать, что кратчайший путь может начинаться в вершине с маленьким охватом, которые мы отбрасываем на каждой итерации. Для того, чтобы принять их во внимание, мы введём новую величину — пенальти(penalty) — верхнюю оценку на длину кратчайшего пути в "отброшенной" зоне.
Пусть — подграф исходного графа, полученный на -й итерации алгоритма, описанного выше. Назовём входящим пенальти (in-penalty) вершины величину , если у было как минимум одно выброшенное в процессе алгоритма входящее ребро, или ноль в противном случае. Аналогично определим исходящее пенальти для исходящих из вершины рёбер.
Изменим алгоритм, чтобы заменить вершины на их пенальти. Для этого переопределим глубину и высоту вершины.
- Глубиной вершины , где — частично обработанное дерево с корнем в величину , где — длина пути от корня до вершины в дереве.
- Чтобы определить высоту вершины, нам нужно понятие "ложных листьев". Для каждой вершины в дереве кратчайших путей добавим потомка — ложный лист, и ребро . В некотором смысле, будет выступать в роли всех рёбер, изначально инцидентных вершине , которые мы отсекли. Тогда высотой вершины будет расстояние от неё, до наиболее далёкого ложного листа. Подчеркнём, что в данный момент ложные листья добавляются неявно, и только после того, как дерево будет частично обработано.
Сокращение путей
Представим последовательность вершин степени 2 с большим охватом, идущих подряд. Добавим, сокращающее ребро (shortcut) — ребро, проходящее из начала пути в его конец с длиной, равной длине этого пути. Таким образом мы можем уменьшить охваты вершин на этом пути и ускорить препроцессинг (уменьшив количество проходимых рёбер), но увеличим память, необходимую для хранения нашего графа.
На этом шаге мы будем искать пропускаемые (bypassable) вершины. Назовём вершину пропускаемой, если выполняется одно из двух условий:
- имеет только одно входящее ребро и одно исходящее ребро
- имеет два входящих ребра , и два исходящих ребра ,
В обоих случаях подразумевается, что , то есть у обязательно есть только два соседа. В первом случае, — кандидат на односторонний пропуск (one-way bypass), во втором — на двухсторонний (two-way bypass). Мы будем использовать сокращающие рёбра, чтобы пропускать такие вершины.
Линия (line) — путь в графе, содержащий как минимум три вершины, так, что все вершины, кроме начальной и конечной, пропускаемые. Каждая пропускаемая вершина может принадлежать только одной линии. Линии также могут быть односторонне- и двухсторонне- пропускаемыми, в зависимости от типа вершин, которые они содержат. Легко заметить, что на линии могут лежать вершины только одного типа.
Как только мы нашли линию, самым простым решением будет добавить одно сокращающее ребро из начала в конец. Но практика показывает, что лучше сократить ещё и входящие в её состав линии меньшего размера, это ещё более уменьшит охваты пропускаемых вершин. Для этого перед добавлением сокращающего ребра по линии, рекурсивно найдём вершину, которая находится примерно на её середине и обработаем левый и правый отрезки как полноценные линии.
Удаление пропущенных вершин
Представим одностороннюю линию, состоящую из трёх вершин , , . Когда мы добавили сокращающее ребро , мы знали, что ребро больше никогда не будет использоваться на кратчайшем пути содержащем подпуть . Кроме того, любой кратчайший путь, содержащий , будет оканчиваться либо в , либо в близлежащей вершине с низким охватом. Тогда, корректной верхней оценкой охвата является . Аналогично, . Зная это, мы можем удалить вершину и смежные ей рёбра из графа и обновить соответствующие значения пенальти для её соседей.
Такую же процедуру можно проделать с двусторонней линией, т.к. помимо оценок, указанных выше, можно добавить:
Фаза отладки
Тот факт, что мы используем пенальти, для ускорения вычисления корректных верхних оценок охвата, приводит к тому, что оценки становятся менее точными в процессе работы алгоритма и с ростом пенальти. Следовательно, для вершин, которые дольше находятся в графе, ошибки накапливаются. Это плохо, потом что такие вершины и являются самыми важными в графе — у них высокий охват, их посещает большое количество кратчайших путей. Если бы мы могли сделать их более точными, во время запроса можно было бы пропустить большее количество вершин.
В этом и заключается цель фазы отладки. После того, как мы найдём верные значения верхних оценок, используя частично обработанные деревья, во время фазы отладки мы пересчитаем охват вершин с наибольшими значениями охвата (в них больше всего ошибок).
Пусть — множество вершин с высоким охватом мощностью . Чтобы пересчитать их охваты, сначала необходимо найти подграф . Этот граф содержит не только первоначальные рёбра, но и добавленные во время основной фазы сокращающие рёбра. Затем мы запустим поиск точных значений охвата для каждой вершины этого подграфа. Так как деревья кратчайших путей будут содержать только вершины из , то нам всё ещё нужно использовать входящие и исходящие пенальти для остальных вершин. Но, тем не менее, они будут меньше, т.к. для самых больших мы подсчитали точное значение охвата.
Во время фазы отладки мы заботимся о точности, а не о скорости, поэтому не добавляем новых сокращающих рёбер и используем точный алгоритм. Поэтому, время работы алгоритма как минимум
Итог
| Метод | Время препроцессинга, м | Память для препроцессинга, MB | Сканируемые запросом вершины, шт | Время запроса, мс |
|---|---|---|---|---|
| Алгоритм Дейкстры | - | 536 | 11 808 864 | 5440,5 |
| ALT(16 ориентиров) | 18 | 2563 | 187 968 | 295,45 |
| Reach | 28 | 893 | 2 405 | 1,77 |
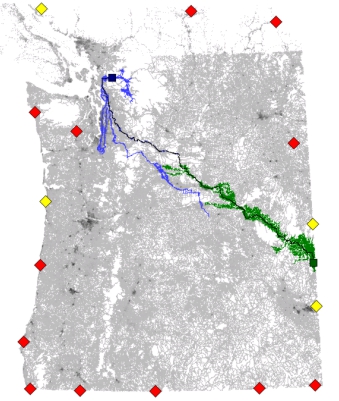
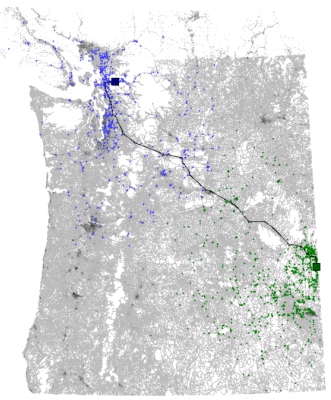
| Алгоритм Дейкстры | ALT (16 ориентиров) | Reach |
|---|---|---|
 |
 |
|
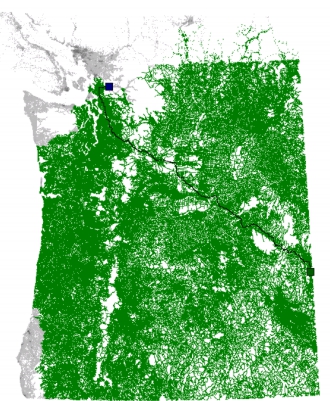
Условные обозначения:
- зелёный квадрат — начало пути
- синий квадрат — конец пути
- зелёные линии — пути, пройденные прямым обходом
- синие линии — пути, пройденные обратным обходом
- красные ромбы — ориентиры
- жёлтые ромбы — выбранные при поиске пути ориентиры