Техника частичного каскадирования — различия между версиями
(Добавлена тема "Построение" с небольшим примером) |
(Синтаксическая поправка) |
||
| Строка 9: | Строка 9: | ||
Пусть <tex> n = \sum\limits_{i = 1}^k n_i </tex>. | Пусть <tex> n = \sum\limits_{i = 1}^k n_i </tex>. | ||
<br> | <br> | ||
| − | 1) | + | 1) Для ответа на запрос последовательно посетим все каталоги. Пусть мы находимся в <tex> i</tex>-ом каталоге, тогда мы можем ответить на запрос для данного каталога за <tex> O(\log n_i) </tex> используя бинарный поиск. Так как каталогов <tex> k </tex> штук, то в итоге мы обработаем запрос за <tex> O(k \log n) </tex>. Для хранения всех каталогов понадобится <tex> \Theta(n) </tex> памяти. |
<br> | <br> | ||
| − | 2) Для второго способа построим сбалансированное бинарное дерево поиска их всех элементов всех каталогов. В каждой вершине дерева будет хранится дополнительно кортеж из <tex> k </tex> элементов - максимальных представителей каталогов меньше либо равных ключу вершины. Таким образом такая структура будет занимать <tex> O(n) </tex> на дерево поиска и <tex> O(kn) </tex> на дополнительные кортежи.Тогда для ответа на запрос | + | 2) Для второго способа построим сбалансированное бинарное дерево поиска их всех элементов всех каталогов. В каждой вершине дерева будет хранится дополнительно кортеж из <tex> k </tex> элементов - максимальных представителей каталогов меньше либо равных ключу вершины. Таким образом такая структура будет занимать <tex> O(n) </tex> на дерево поиска и <tex> O(kn) </tex> на дополнительные кортежи.Тогда для ответа на запрос найдем в дереве поиска максимальный ключ меньше либо равный <tex> x </tex> и выведем <tex> k </tex> элементов соответствующего кортежа, итого ответ на запрос производится за <tex> O(\log n + k) </tex>. |
<br> <br> | <br> <br> | ||
Итого имеем: | Итого имеем: | ||
Версия 19:13, 7 июня 2017
Техника частичного каскадирования (англ. fractional cascading technique) — это способ организации структуры данных, который предназначен для быстрого итеративного поиска в каталогах.
| Задача: |
| Дано каталогов , каталог представляет собой упорядоченный массив размера . Поступают запросы, которые представляют собой один элемент . Требуется для каждого запроса определить в каждом каталоге максимальный элемент меньше либо равный . |
Различные подходы к решению
Пусть .
1) Для ответа на запрос последовательно посетим все каталоги. Пусть мы находимся в -ом каталоге, тогда мы можем ответить на запрос для данного каталога за используя бинарный поиск. Так как каталогов штук, то в итоге мы обработаем запрос за . Для хранения всех каталогов понадобится памяти.
2) Для второго способа построим сбалансированное бинарное дерево поиска их всех элементов всех каталогов. В каждой вершине дерева будет хранится дополнительно кортеж из элементов - максимальных представителей каталогов меньше либо равных ключу вершины. Таким образом такая структура будет занимать на дерево поиска и на дополнительные кортежи.Тогда для ответа на запрос найдем в дереве поиска максимальный ключ меньше либо равный и выведем элементов соответствующего кортежа, итого ответ на запрос производится за .
Итого имеем:
| Тип подхода к решению | Необходимая память | Время ответа на один запрос |
|---|---|---|
| |
|
|
| |
|
|
Решение с помощью техники частичного каскадирования
Как будет показано далее, эта техника берет лучшее от подходов к решению этой задачи, что были рассмотрены выше, а именно она требует памяти и времени для ответа на запрос.
Идея данной техники построена на следующем:
1) Мы можем проводить ссылки из каталога номер в -ый каталог таким образом, что разница между элементами соединенными ссылками минимальна, что, очевидно, в некоторых случаях уменьшит время поиска.
2) Мы можем для оптимизации пункта 1 создать модифицированные каталоги , где -ый каталог будет представлять каталог слитый с
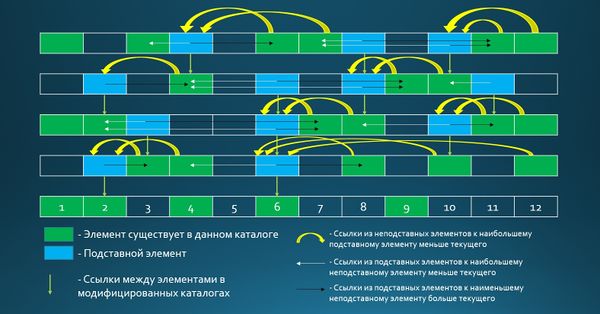
Построение
Рассмотрим подробнее построение каталогов . Введем определения:
| Определение: |
| Подставной элемент — элемент каталога , который пришел из каталога . А также каталоги будем называть модифицированными каталогами. |
Первый этап построения:
: Данный каталог не имеет никаких ссылок и равен .
: Для построения данного каталога будем сливать каталог с каждым вторым элементом каталога . Каждый элемент из каталога оснастим ссылкой на позицию, откуда мы его взяли.
Второй этап построения:
В каждом модифицированном каталоге для каждого элемента заведем две ссылки. Для неподставных элементов это будут ссылки на минимальный подставной элемент больше текущего и на максимальный подставной элемент меньше текущего. И наоборот, если элемент подставной, то ссылки будут на минимальный неподставной элемент больше текущего и на максимальный неподставной элемент больше текущего.
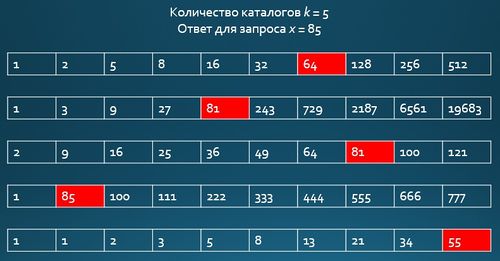
Рассмотрим на процесс построения на примере.
Пусть дано каталогов :
Для наглядности заведем таблицу, где в -ой строке -ая ячейка будет окрашена в зеленый цвет, если она присутствует в каталоге . Тогда результатом построения будет таблица, которая представлена на рисунке (без ссылок из подставных элементов).