Панциклический граф

Определение:

Панциклический граф (англ. pancyclic graph) — граф, в котором есть циклы всех длин от [math] 3 [/math] до [math] n [/math] . Если граф содержит все циклы от [math] r [/math] до [math] n [/math], то такой граф называют [math] r [/math]-панциклическим.

Предпосылки к теореме. Теорема Мантела(частный случай теоремы Турана) утверждает, что для любого граф на [math] n [/math] вершинах, у которого количество ребер не меньше [math] \genfrac{}{}{}{0}{n^2}{4} [/math], либо содержит треугольник либо является [math]K_{\genfrac{}{}{}{}{n}{2}, \genfrac{}{}{}{}{n}{2}}[/math].

Теорема (J. A. Bondy):

[math]G(V, E) [/math] — гамильтонов граф, [math]|V| = n, |E| \geqslant \genfrac{}{}{}{0}{n^2}{4} [/math]. Тогда верно одно из двух утверждений: [math] G [/math] — панциклический граф [math] G [/math] = [math]K_{\genfrac{}{}{}{}{n}{2}, \genfrac{}{}{}{}{n}{2}}[/math]

Доказательство:

[math]\triangleright[/math]

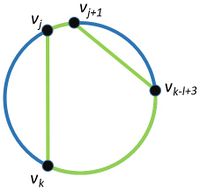
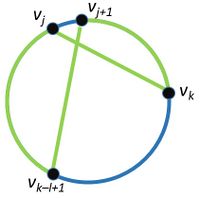
Обозначим как [math] C=v_1 v_2 v_3 \ldots v_n [/math] гамильтонов цикл в графе [math] G [/math]. Для простоты расположим [math] C [/math] на окружности.Также подразумевается, что все индексы при вершинах берутся по модулю, т.е. [math] v_j = v_{((j - 1)\bmod n) + 1} [/math]. Пусть в графе нет цикла длины [math] l [/math], [math] 3 \leqslant l \leqslant n-1 [/math] (по условию в графе существует гамильтонов цикл, длина которого равна [math] n [/math]). Рассмотрим две соседние вершины [math] v_i v_{i+1} [/math] и вместе с ними рассмотрим следующие пары: Для [math]k[/math] таких, что [math] v_k [/math] лежит на дуге [math] (v_{j + l - 1}, v_{j + l}, v_{j -1}) [/math] рассмотрим пары ([math]v_j, v_k[/math]) и ([math]v_{j+1}, v_{k-l+3}[/math]) (см. рисунок слева) Для [math]k[/math] таких, что [math] v_k [/math] лежит на дуге [math] (v_{j + 2}, v_{j + 3}, v_{j + l - 2}) [/math] рассмотрим пары ([math]v_j, v_k[/math]) и ([math]v_{j+1}, v_{k-l+1}[/math]) (см. рисунок справа) При добавлении таких пар ребер в графе появляется цикл длины [math] l [/math], а значить в [math] G [/math] может входить максимум одно ребро из таких пар. Тогда можно утверждать, что [math] deg(v_j) + deg(v_{j + 1}) \leqslant n [/math]. Докажем методом от противного, что [math] n [/math] — четно. Пусть [math] n [/math] является нечетным, тогда из рассуждений выше существует вершина [math] v_x [/math], для которое верно, что [math] deg(v_x) \leqslant \genfrac{}{}{}{0}{n-1}{2} [/math]. Пусть это не так, тогда [math] \forall i, 1 \leqslant i \leqslant n : deg(v_i) \geqslant \genfrac{}{}{}{0}{n-1}{2} + 1 = \genfrac{}{}{}{0}{n+1}{2} [/math], значит [math] \forall j, 1 \leqslant j \leqslant n : deg(v_j) + deg(v_{j+1}) \geqslant \genfrac{}{}{}{0}{n+1}{2} + \genfrac{}{}{}{0}{n+1}{2} = n + 1 [/math], то есть мы получили противоречие с тем, что [math] deg(v_j) + deg(v_{j + 1}) \leqslant n [/math]. Без потери общности пусть [math] v_x = v_n [/math]. Рассмотрим [math] 2|E| = \sum\limits_{i=1}^n deg(v_i) = \sum\limits_{i=1}^{\genfrac{}{}{}{}{n - 1}{2}} (deg(v_{2i-1}) + deg(v_{2i})) + deg(v_n) \leqslant \genfrac{}{}{}{0}{n(n-1)}{2} + [/math] [math] \genfrac{}{}{}{0}{n-1}{2} \lt \genfrac{}{}{}{0}{n^2}{2} [/math], то есть [math] |E| \lt \genfrac{}{}{}{0}{n^2}{4} [/math], но по условию [math] |E| \geqslant \genfrac{}{}{}{0}{n^2}{4} [/math] — получили противоречие. Таким образом [math] n [/math] является четным. Тогда верно, что [math] 2|E| \leqslant \sum\limits_{i=1}^n deg(v_i) = \sum\limits_{i=1}^{n/2} (deg(v_{2i-1}) + deg(v_{2i})) \leqslant \genfrac{}{}{}{0}{n^2}{2} [/math], а так как по условию [math] |E| \geqslant \genfrac{}{}{}{0}{n^2}{4} [/math], то [math] |E| = \genfrac{}{}{}{0}{n^2}{4} [/math]. Данное равенство достигается, если верно, что: [math] v_k [/math] лежит на дуге [math] (v_{j + l - 1}, v_{j + l}, v_{j - 1}) [/math]: [math] (v_j, v_k) \in E [/math] и [math](v_{j+1}, v_{k-l+3}) \notin E [/math] [math] v_k [/math] лежит на дуге [math] (v_{j + 2}, v_{j + 3}, v_{j + l - 2}) [/math]: [math](v_j, v_k) \in E [/math] и [math](v_{j+1}, v_{k-l+1}) \notin E [/math] Пусть [math] G [/math] не [math] K_{n/2, n/2} [/math], 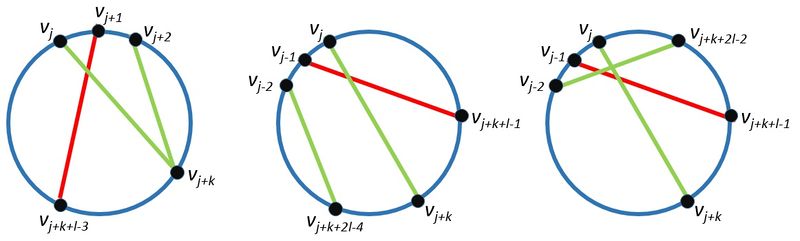тогда существует такое четное число [math] k [/math], что в графе [math] G [/math] существует ребро [math] (v_j, v_{j+k}) [/math], т.е. существует цикл нечетной длины. Докажем, что в таком случае существует ребро [math] (v_j, v_{j+2}) \in E [/math]. Пусть это не так и минимальное четное [math] k [/math], что [math] \exists (v_j, v_{j+k}) \in E [/math] больше двух, т.е. [math] k \geqslant 4 [/math]. Тогда существует три случая: [math] 4 \leqslant k \leqslant n - l [/math] [math] (v_j, v_{j+k}) \in E \Rightarrow (v_{j+1}, v_{j+k+l-3}) \notin E \Rightarrow (v_{j+2}, v_{j+k}) \in E [/math] [math] \exists l = k-2 : (v_i, v_{i+l}) \in E [/math] — противоречие с минимальностью [math] k [/math] [math] n - l + 2 \leqslant k \leqslant 2n - 2l [/math] [math] (v_j, v_{j+k}) \in E \Rightarrow (v_{j-1}, v_{j+k+l-1}) \notin E \Rightarrow (v_{j-2}, v_{j+k+2l-4}) \in E [/math] однако [math] 2n - k - 2l + 2 \leqslant k - 2 [/math] — противоречие с минимальностью [math] k [/math] [math] 2n - 2l + 2 \leqslant k \leqslant n - 2 [/math] [math] (v_j, v_{j+k}) \in E \Rightarrow (v_{j-1}, v_{j+k+l-1}) \notin E \Rightarrow (v_{j-2}, v_{j+k+2l-2}) \in E [/math] однако [math] k + 2l - 2n \leqslant k - 2 [/math] — снова проиворечие с минимальностью выбранного k Таким образом, в [math] G [/math] существует ребро [math] (v_j, v_{j+2}) [/math], но тогда [math] (v_j, v_{j+l}) \notin E [/math], а следовательно [math] (v_{j+1}, v_{j+3}) \in E [/math]. Если продолжить по всему графу, то получим, что [math] \forall j : (v_j, v_{j+2}) \in E [/math] и, как следствие, [math] G [/math] — панциклический.

[math]\triangleleft[/math]

Утверждение:

[math]G(V, E), |V| = n , |E| = m, \forall (u, v) \notin E : deg(u) + deg(v) \geqslant n [/math] Тогда верно одно из двух утверждений: [math] G [/math] — панциклический граф [math] G [/math] = [math]K_{\genfrac{}{}{}{}{n}{2}, \genfrac{}{}{}{}{n}{2}}[/math]

[math]\triangleright[/math]

По теореме Оре [math] G [/math] — гамильтонов граф. Покажем, что [math] m \geqslant \genfrac{}{}{}{0}{n^2}{4} [/math]. Пусть [math] k [/math] — минимальная степень вершины в графе. [math] k \geqslant \genfrac{}{}{}{0}{n}{2} [/math], тогда [math] 2m = \sum\limits_{i=1}^n deg(v_i) \gt = \sum\limits_{i=1}^n k = k n \geqslant \genfrac{}{}{}{0}{n^2}{2} [/math] [math] k \lt \genfrac{}{}{}{0}{n}{2} [/math]. Пусть существует [math] x [/math] вершин, так что их степени равны [math] k [/math], тогда они все должны быть связаны, так как иначе мы получим противоречие с утверждением теоремы [math] \forall (u, v) \notin E : deg(u) + deg(v) \geqslant n [/math]. Понятно, что [math] x \leqslant k + 1 [/math], но так как граф является гамильтоновым, то он связен, а значит [math] x \lt k + 1 [/math]. Несложно заметить, что если из всех [math] x [/math] вершин степени [math] k [/math] провести оставшиеся ребра в одну вершину, у которой степень больше, то в графе остенется как минимум [math] n - k - 1 [/math] вершин, степени которых как минимум [math] n - k [/math], поскольку должно выполняться неравенство из теоермы. Тогда можно оценить количество ребер. [math] m \geqslant \genfrac{}{}{}{0}{1}{2}((n-k-1)(n-k)+k^2+(k+1)) = \genfrac{}{}{}{0}{1}{2}(n^2 - n(2k + 1) + 2k^2 + 2k + 1) \geqslant \genfrac{}{}{}{0}{n^2+1}{4} [/math] Таким образом [math] m \geqslant \genfrac{}{}{}{0}{n^2}{4} [/math] и согласно теореме граф либо панциклический, либо [math]K_{\genfrac{}{}{}{}{n}{2}, \genfrac{}{}{}{}{n}{2}}[/math].

[math]\triangleleft[/math]

См. также

• Теорема Оре
• Гамильтоновы графы

Источники информации

• J.A. Bondy — Pancyclic Graphs I*
• Д.В. Карпов — Теория графов.