Симуляция одним распределением другого — различия между версиями
(→Распределение) (Метки: правка с мобильного устройства, правка из мобильной версии) |
(→Распределение) (Метки: правка с мобильного устройства, правка из мобильной версии) |
||
| Строка 6: | Строка 6: | ||
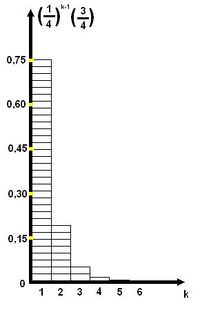
[[Файл:Распределение1_4.JPG|200px|thumb|right|Геометрическое распределение с <tex>p = \dfrac {3} {4}</tex>]] | [[Файл:Распределение1_4.JPG|200px|thumb|right|Геометрическое распределение с <tex>p = \dfrac {3} {4}</tex>]] | ||
| − | + | Закон распределения дискретной случайной величины <tex>\xi</tex> задается таблицей: | |
| + | |||
<tex>\xi: \begin{pmatrix} | <tex>\xi: \begin{pmatrix} | ||
x_1 & x_2 & \ldots & x_n \\ | x_1 & x_2 & \ldots & x_n \\ | ||
Версия 19:44, 13 марта 2018
Содержание
Распределение
| Определение: |
| Распределение вероятностей — закон, описывающий область значений случайной величины и вероятность их исхода. |
Закон распределения дискретной случайной величины задается таблицей:
где — всевозможные значения величины а — их вероятности, то есть
При этом должно выполняться равенство:
Это равенство означает, что при испытании одно из значений заведомо реализуется. Таблица показывает, как суммарная вероятность распределяется по возможным значениям случайной величины.
Для непрерывных случайных величин задание закона распределения в виде такой таблицы невозможно, поэтому его задают двумя другими способами:
- С помощью функции распределения
- С помощью плотности вероятности
Примеры распределений
Биномиальное распределение (закон Бернулли)
| Определение: |
| Дискретная случайная величина называется биномиальной с параметрами если она принимает значения от до и вероятности вычисляются по формуле |
Нормальное распределение (распределение Гаусса)
| Определение: |
| Непрерывную случайную величину называют нормальной с параметрами и пишут если ее плотность вероятности дается формулой |
Равномерное распределение
| Определение: |
| Непрерывная случайная величина называется равномерно распределенной на если ее плотность вероятности дается формулой |
Симуляция распределений
Для того, чтобы создать необходимое распределение вероятностей, достаточно иметь последовательность независимых случайных величин типа "честной монеты".
Например, для создания схемы с двумя исходами $A_1$ и $A_2$: $P(A_1)=\dfrac{3}{4}$ $,$ $P(A_2)=\dfrac{1}{4}$ можно из датчика случайных двоичных величин получить два результата "честной монеты" $\delta_1$ и $\delta_2$ и, например, при $\delta_1 = \delta_2 = 1$ выработать исход $A_2$, а в остальных случаях $A_1$.
Аналогично для схемы с четырьмя исходами $P(A_1)=\dfrac{3}{16}$ $,$ $P(A_2)=\dfrac{1}{16}$ $,$ $P(A_3)=\dfrac{8}{16}$ $,$ $P(A_4)=\dfrac{4}{16}$ можно получить четыре результата "честной монеты" $\delta_1$ $,$ $\delta_2$ $,$ $\delta_3$ $,$ $\delta_4$ и любым способом сопоставить трём из 16 возможных наборов исход $A_1$, одному $-$ $A_2$, восьми $-$ $A_3$, четырём $-$ $A_4$.
Если же вероятности исходов не кратны $2^{-k}$, можно применить два различных варианта действий.
- Можно приблизить вероятности двоичными дробями (с любой точностью), далее работать с полученными приближёнными значениями
- Пусть все вероятности $n_i$ $-$ дроби со знаменателем $r$. Найдём $k$, для которого $r < 2^k$. Предложим схему с $k$ результатами "честной монеты", в которой $r$ наборов используются для выработки случайного исхода, а остальные $2^{k}-r$ наборов объявляются "неудачными" и требуют повторного эксперимента (пока не встретится удачный). Чем выше доля полезных исходов равная $r2^{-k}$, тем схема будет эффективнее.
Количество результатов "честной монеты" $\lambda$, которые необходимы для формирования случайного исхода, $-$ это случайная величина. Её математическое ожидание:
$E\lambda = \dfrac{1}{2}\cdot1+\dfrac{1}{4}\cdot2+\dfrac{1}{8}\cdot3+\dfrac{1}{16}\cdot3+\dfrac{1}{16}\cdot4 = 1\dfrac{7}{8}$
Можно сделать схему более экономной, используя свойство датчика случайных чисел формировать не отдельные результаты "честной монеты", а целые наборы их, например в виде числа, равномерно распределённого в $[0, 1]$. Образуем по данному набору вероятностей $p_i$ накопленные суммы $s_i$: $s_0 = 0; s_i = s_{i-1} + p_i, i > 0$. Случайный исход будет вырабатываться так: по полученному из датчика случайному числу $\gamma$ определяется такой индекс $i$, для которого $s_{i-1} < \gamma \leqslant s_i$. Найденное значение индекса $i$ и определяет исход $A_i$.
Индекс $i$ можно определять непосредственно просмотром $s_i$ подряд. Если $k$ велико, можно применять специальные приёмы ускоренного поиска, например, деление множества индексов примерно пополам.
Общий случай
| рис. | рис. | рис. |
 |
 |
|
Допустим у нас есть распределение Нам нужно получить распределение .
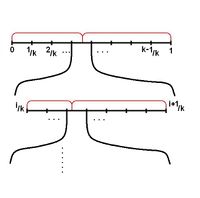
Для начала рассмотрим случай, когда все а в распределении количество элементарных исходов равно рис.
Проводим эксперимент: если попадаем в область пересекающуюся с и то увеличиваем ее и повторяем эксперимент. На рис. красным обозначено распределение Вероятность того, что на этом шаге эксперимент не закончится — Математическое ожидание количества экспериментов — при
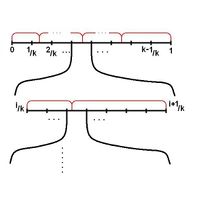
Теперь рассмотрим случай, когда все элементарные исходы по-прежнему равновероятны а количество элементарных исходов распределения равно рис. Повторим эксперимент раз.
Отрезок разбился на отрезков. Стык будет не более, чем в половине отрезков. Математическое ожидание количества экспериментов
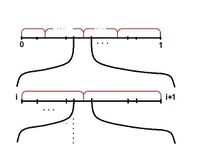
Берем , и пусть оно максимальной длины рис. Проводим экспериментов. все остальные еще меньше. Суммарная длина отрезков не больше Нужно
Таким образом, из любого исходного распределения можно получить нужное нам распределение.
См. также
Литература
- Боровков А.А. Математическая статистика: оценка параметров, проверка гипотез. — М., Физматлит, 1984, — стр. 71.
- Т. Кормен, Ч. Лейзерсон, Р. Ривест, К. Штайн — Алгоритмы. Построение и анализ — М. : ООО "И. Д. Вильямс", 2013. — 1328 с. — стр. 1254.
- Романовский И. В. — Элементы теории вероятностей и математической статистики (теория и задачи): учебное пособие. — Омск, издатель ИП Скорнякова Е.В., 2012. — 189 с. — стр. 34.