Переобучение — различия между версиями
Rugpanov (обсуждение | вклад) (Улучшить картинки: подписи) |
Rugpanov (обсуждение | вклад) м (Поправить номера риссунков) |
||
| Строка 4: | Строка 4: | ||
== Примеры == | == Примеры == | ||
=== Недообучение на примере линейной регрессии === | === Недообучение на примере линейной регрессии === | ||
| − | Представьте задачу предсказания y по x ∈ R. Рис 1 показывает результат использования модели <math>y=θ_0+θ_1*x</math> для представленного датасета. Как видно из Рис 1 данные не поддаются линейной зависимости и по | + | Представьте задачу предсказания y по x ∈ R. Рис 1 показывает результат использования модели <math>y=θ_0+θ_1*x</math> для представленного датасета. Как видно из Рис 1 данные не поддаются линейной зависимости и по этой причине модель не очень хороша. |
{|align="center" | {|align="center" | ||
|-valign="top" | |-valign="top" | ||
| Строка 23: | Строка 23: | ||
=== Переобучение на примере линейной регрессии === | === Переобучение на примере линейной регрессии === | ||
| − | Представьте задачу предсказания y по x ∈ R. Рис | + | Представьте задачу предсказания y по x ∈ R. Рис 5 показывает результат использования модели <math>y=θ_0+θ_1*x+θ_2*x^2+θ_3*x^3+θ_4*x^4</math> для представленного датасета. Как видно из Рис 5 данная модель слишком заточена для обучающего датасета и, веротяно, покажет плохой результат на тестовой. |
{|align="center" | {|align="center" | ||
|-valign="top" | |-valign="top" | ||
| Строка 29: | Строка 29: | ||
|[[Файл:Normal_bias_reg.png|200px|thumb|Рис 6]] | |[[Файл:Normal_bias_reg.png|200px|thumb|Рис 6]] | ||
|} | |} | ||
| − | Если же добавить упростить модель, и использовать функцию <math>y=θ_0+θ_1*x+θ_2*x^2</math>, как представлено на Рис | + | Если же добавить упростить модель, и использовать функцию <math>y=θ_0+θ_1*x+θ_2*x^2</math>, как представлено на Рис 6, то модель значительно лучше подходит для представленного датасета. |
=== Переобучение на примере логистической регрессии === | === Переобучение на примере логистической регрессии === | ||
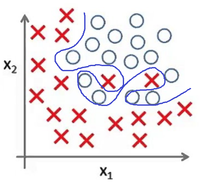
| − | Представьте задачу классификации размеченых точек. Рис | + | Представьте задачу классификации размеченых точек. Рис 7 показывает результат использования модели <math>g(θ_0+θ_1*x_1+θ_2*x_1^2+θ_3*x_2*x_1^2+θ_4*x_1^2*x_2^2 + ...)</math> для представленного датасета. |
{|align="center" | {|align="center" | ||
|-valign="top" | |-valign="top" | ||
| Строка 38: | Строка 38: | ||
|[[Файл:Normal_bias_cla.png|200px|thumb|Рис 8]] | |[[Файл:Normal_bias_cla.png|200px|thumb|Рис 8]] | ||
|} | |} | ||
| − | В случае же выбора модели <math>g(θ_0+θ_1*x_1+θ_2*x_2+θ_3*x_1^2+θ_4*x_2^2+x_1*x_2)</math>, представленой на Рис | + | В случае же выбора модели <math>g(θ_0+θ_1*x_1+θ_2*x_2+θ_3*x_1^2+θ_4*x_2^2+x_1*x_2)</math>, представленой на Рис 8, данные значительно лучше соответствуют модели. |
== Кривые обучения == | == Кривые обучения == | ||
Версия 15:04, 14 октября 2018
Переобучение (англ. overfitting, high variance) - негативное явление возникающее, когда величина средней ошибки обученного алгоритма на объектах тестовой выборки оказывается существенно выше, чем величина средней ошибки на обучающей выборке. Переобучение возникает при использовании избыточно сложных моделей.
Недообучение (англ. underfitting, high bias) - негативное явление возникающее, когда алгоритм обучения не обеспечивает достаточно малой величины средней ошибки на обучающей выборке. Недообучение возникает при использовании недостаточно сложных моделей.
Содержание
Примеры
Недообучение на примере линейной регрессии
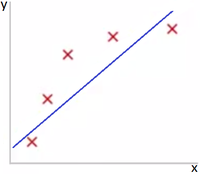
Представьте задачу предсказания y по x ∈ R. Рис 1 показывает результат использования модели для представленного датасета. Как видно из Рис 1 данные не поддаются линейной зависимости и по этой причине модель не очень хороша.
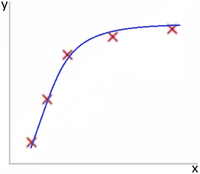
Если же добавить дополнительный параметр x^2, и использовать модель , как представлено на Рис 2, то модель значительно лучше подходит для представленного датасета.
Недообучение на примере логистической регрессии
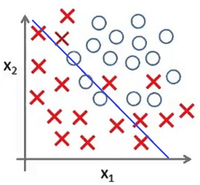
Представьте задачу классификации размеченых точек. Рис 3 показывает результат использования модели для представленного датасета. Как и в предыдущем примере данные не поддаются классификации по линейной зависимости.
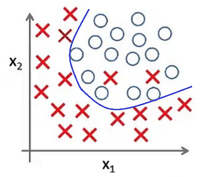
В случае же выбора модели , представленой на Рис 4, данные значительно лучше соответствуют модели.
Переобучение на примере линейной регрессии
Представьте задачу предсказания y по x ∈ R. Рис 5 показывает результат использования модели для представленного датасета. Как видно из Рис 5 данная модель слишком заточена для обучающего датасета и, веротяно, покажет плохой результат на тестовой.
Если же добавить упростить модель, и использовать функцию , как представлено на Рис 6, то модель значительно лучше подходит для представленного датасета.
Переобучение на примере логистической регрессии
Представьте задачу классификации размеченых точек. Рис 7 показывает результат использования модели для представленного датасета.
В случае же выбора модели , представленой на Рис 8, данные значительно лучше соответствуют модели.
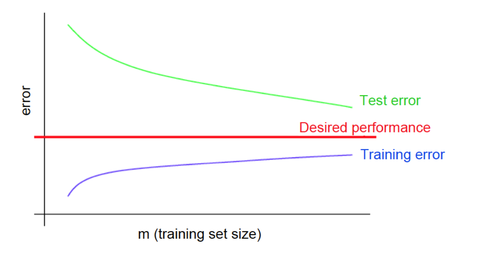
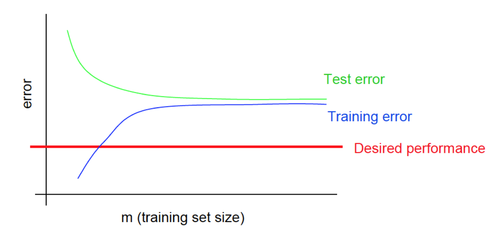
Кривые обучения
Кривые обучения при переобучении
Кривые обучения при недообучении
Возможные решения
Возможные решения при переобучении
- Увеличение данных датасета
- Уменьшение количества параметров
- Добавление регуляризации / увеличение коэффициента регуляризации
Возможные решения при недообучении
- Добавление новых параметров
- Использование для описания модели функций с более высокой степенью
- Уменьшение коэффициента регуляризации