Generative Adversarial Nets (GAN) — различия между версиями

Материал из Викиконспекты
Перейти к: навигация, поиск
Строка 1: Строка 1:
 
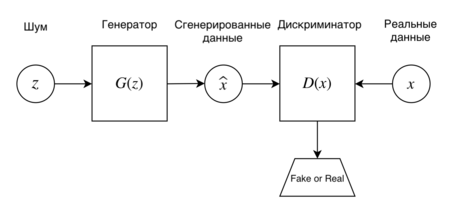
[[File:Арх_ган.png|450px|thumb|Оригинальная архитектура GAN]]
 
[[File:Арх_ган.png|450px|thumb|Оригинальная архитектура GAN]]
−
'''Порождающие состязательные сети''' (англ. ''Generative Adversarial Nets, GAN'') {{---}} это алгоритм машинного обучения, входящий в семейство [[:Порождающие модели|порождающих моделей]]<sup>[на 14.11.18 не создан]</sup> и построенный на комбинации из двух нейронных сетей, одна из которых генерирует образцы, а другая же пытается отличить настоящие образцы от сгенерированных. Впервые такие сети были представлены Иэном Гудфеллоу в 2014 году.  
+
'''Порождающие состязательные сети''' (англ. ''Generative Adversarial Nets, GAN'') {{---}} это алгоритм машинного обучения, входящий в семейство [[:Порождающие модели|порождающих моделей]]<sup>[на 14.11.18 не создан]</sup> и построенный на комбинации из двух нейронных сетей, одна из которых генерирует образцы, другая пытается отличить настоящие образцы от сгенерированных. Впервые такие сети были представлены Иэном Гудфеллоу в 2014 году.  
  
 
==Постановка задачи и метод==
 
==Постановка задачи и метод==

Версия 17:01, 14 ноября 2018

Оригинальная архитектура GAN

Порождающие состязательные сети (англ. Generative Adversarial Nets, GAN) — это алгоритм машинного обучения, входящий в семейство порождающих моделей[на 14.11.18 не создан] и построенный на комбинации из двух нейронных сетей, одна из которых генерирует образцы, другая пытается отличить настоящие образцы от сгенерированных. Впервые такие сети были представлены Иэном Гудфеллоу в 2014 году.

Постановка задачи и метод

Имеется множество образцов [math]X[/math] из распределения [math]p_{data}[/math], заданного на [math] \mathbb R^n [/math], а также некоторое пространство латентных факторов [math]Z[/math] из распределения [math]p_{z}[/math], например, случайные вектора из равномерного распределения [math] \mathbb U^p(0,1) [/math].

Рассмотрим две нейронные сети: первая — генератор [math] G: Z \rightarrow \mathbb R^n [/math] с параметрами [math]\theta[/math], цель которой сгенерировать похожий образец из [math]p_{data}[/math], и вторая — дискриминатор [math]D: \mathbb R^n \rightarrow \mathbb [0,1] [/math] с параметрами [math]\gamma[/math], цель которой выдавать максимальную оценку на образцах из [math]X[/math] и минимальную на сгенерированных образцах из [math]G[/math]. Распределение, порождаемое генератором будем обозначать [math]p_{gen}[/math]. Так же заметим, что в текущем изложении не принципиальны архитектуры нейронных сетей, поэтому можно считать, что параметры [math]\theta[/math] и [math]\gamma[/math] являются просто параметрами многослойных персептронов.

В качестве примера можно рассматривать генерацию реалистичных фотографий: в этом случае, входом для генератора может быть случайный многомерный шум, а выходом генератора (и входом для дискриминатора) RGB-изображение; выходом же для дискриминатора будет вероятность, что фотография настоящая, т.е число от 0 до 1.

Наша задача выучить распределение [math]p_{gen}[/math] так, чтобы оно как можно лучше описывало [math]p_{data}[/math]. Зададим функцию ошибки для получившейся модели. Со стороны дискриминатора мы хотим распознавать образцы из [math]X[/math] как правильные, т.е в сторону единицы, и образцы из [math]G[/math] как неправильные, т.е в сторону нуля, таким образом нужно максимизировать следующую величину:

[math]\mathop{E}\limits_{x \sim p_{data}}[logD(x)] + \mathop{E}\limits_{x \sim p_{gen}}[log(1-D(x))][/math], где [math]\mathop{E}\limits_{x \sim p_{gen}}[log(1-D(x))] = \mathop{E}\limits_{z \sim p_{z}}[log(1-D(G(z))][/math]

Со стороны же генератора требуется научиться "обманывать" дискриминатор, т.е минимизировать по [math]p_{gen}[/math] второе слагаемое предыдущего выражения. Другими словами, [math]G[/math] и [math]D[/math] играют в так называемую минимаксную игру, решая следующую задачу оптимизации:

[math] \min\limits_{G}\max\limits_{D} \mathop{E}\limits_{x \sim p_{data}}[logD(x)] + \mathop{E}\limits_{z \sim p_{z}}[log(1-D(G(z))] [/math]

Теоретическое обоснование того, что такой метод заставляет [math]p_{gen}[/math] сходится к [math]p_{data}[/math] описано в исходной статье. [1]

Оригинальный алгоритм обучения GAN

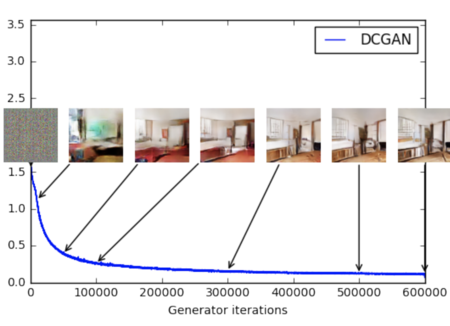
Визуализация генерирования фотографии с помощью DCGAN по одному и тому же шуму в зависимости от итерации обучения. Источник: https://arxiv.org/pdf/1701.07875.pdf

В процессе обучения требуется делать два шага оптимизации поочередно: сначала обновлять веса генератора [math]\theta[/math] при фиксированном [math]\gamma[/math], а затем веса дискриминатора [math]\gamma[/math] при фиксированном [math]\theta[/math]. На практике дискриминатор обновляется [math]k[/math] раз вместо одного; [math]k[/math] является гиперпараметром. 

// num_iteration — число итераций обучения 
for i = 1..num_iteration do
  for j = 1..k do
    Сэмплируем мини-батч $\{z_1, . . . , z_m\}$ из распределения $p_z$.
    Сэмплируем мини-батч $\{x_1, . . . , x_m\}$ из распределения $p_{data}$.
    Обновляем дискриминатор в сторону возрастания его градиента:
    [math]\mathop{\nabla}_{\gamma} { \frac{1}{m} \sum_{t = 1}^m \limits} [logD(x_t)]  + [log(1-D(G(z_t))] [/math]
  end for 
  Сэмплируем мини-батч $\{z_1, . . . , z_m\}$ из распределения $p_z$.  
  Обновляем генератор в сторону убывания его градиента:
  [math]\mathop{\nabla}_{\theta}  { \frac{1}{m} \sum_{t = 1}^m \limits} [log(1-D(G(z_t))] [/math]
end for

Обновления на основе градиента могут быть сделаны любым стандартным способом, например, в оригинальной статье использовался стохастический градиентный спуск[на 14.11.18 не создан] с импульсом.

Улучшение обучения GAN

Большинство GAN'ов подвержено следующим проблемам:

  • Несходимость (non-convergence): параметры модели дестабилизируются и не сходятся,
  • Схлопывание мод распределения (mode collapse): генератор коллапсирует, т.е выдает ограниченное количество разных образцов,
  • Исчезающий градиент (diminished gradient): дискриминатор становится слишком "сильным", а градиент генератора исчезает и обучение не происходит,
  • Высокая чувствительность к гиперпараметрам.

Универсального подхода к их решению нет, но существуют практические советы[2], которые могут помочь. Основными из них являются:

  1. Нормализация данных. Все признаки в диапазоне $[-1; 1]$.
  2. Замена функции ошибки для $G$ с $\min log (1-D)$ на $\max log D$, потому что исходный вариант имеет маленький градиент на раннем этапе обучения и большой градиент при сходимости, а предложенный наоборот.
  3. Сэмплирование из многомерного нормального распределения вместо равномерного.
  4. Использовать нормализационные слои (например, batch normalization или layer normalization) в $G$ и $D$.
  5. Использовать метки для данных, если они имеются, т.е обучать дискриминатор еще и классифицировать образцы.

Применение

Прогресс в генерации фотографий с помощью GAN. Источник: https://twitter.com/goodfellow_ian

Чаще всего GAN'ы используются для генерации реалистичных фотографий. Серьезные улучшения в этом направлении были сделаны следующими работами:

  • Auxiliary GAN[3]: вариант GAN-архитектуры, использующий метки данных.
  • SN-GAN[4]: GAN с новым подходом решения проблемы нестабильного обучения через спектральную нормализацию.
  • SAGAN[5]: GAN, основанный на механизме внимания.
  • BigGAN[6]: GAN с ортогональной регуляризацией, позволившей разрешить проблему коллапсирования при долгом обучении.

Кроме простой генерации изображений, существуют достаточно необычные применения, дающие впечатляющие результаты не только на картинках, но и на звуке:

  • CycleGAN[7]: меняет изображения c одного домена на другой, например, лошадей на зебр,
  • SRGAN[8]: создает изображения с высоким разрешением из более низкого разрешения,
  • Pix2Pix[9]: создает изображения по семантической окраске,
  • StackGAN[10]: создает изображения по заданному тексту,
  • MidiNet[11]: генерирует последовательность нот, таким образом, создает мелодию.

См. также

Примечания

  1. ↑ Ian J. Goodfellow — Generative Adversarial Nets
  2. ↑ How to Train a GAN? Tips and tricks to make GANs work
  3. ↑ Augustus Odena — Conditional Image Synthesis with Auxiliary Classifier GANs
  4. ↑ Takeru Miyato — SPECTRAL NORMALIZATION FOR GENERATIVE ADVERSARIAL NETWORKS
  5. ↑ Han Zhang — Self-Attention Generative Adversarial Networks
  6. ↑ Andrew Brock — LARGE SCALE GAN TRAINING FOR HIGH FIDELITY NATURAL IMAGE SYNTHESIS
  7. ↑ Jun-Yan Zhu & Taesung Park — Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks
  8. ↑ Christian Ledig — Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network
  9. ↑ Phillip Isola — Image-to-Image Translation with Conditional Adversarial Nets
  10. ↑ Han Zhang — StackGAN: Text to Photo-realistic Image Synthesis with Stacked Generative Adversarial Networks
  11. ↑ Li-Chia Yang — MIDINET: A CONVOLUTIONAL GENERATIVE ADVERSARIAL NETWORK FOR SYMBOLIC-DOMAIN MUSIC GENERATION

Источники информации

Источник — «http://neerc.ifmo.ru/wiki/index.php?title=Generative_Adversarial_Nets_(GAN)&oldid=66976»