Метрический классификатор и метод ближайших соседей — различия между версиями
Kirant (обсуждение | вклад) |
Kirant (обсуждение | вклад) |
||
| Строка 83: | Строка 83: | ||
== Пример использования (через scikit-learn) == | == Пример использования (через scikit-learn) == | ||
| − | + | Рассмотрим использование алгоритма knn на примере [https://archive.ics.uci.edu/ml/datasets/Breast+Cancer+Wisconsin+%28Diagnostic%29 реального датасета]. | |
| + | Предположим, что мы загрузили ''wdbc.data'' и сохранили как ''tr.csv'' с загаловком - описанием признаков. | ||
| + | |||
| + | * Загружаем данные | ||
| + | |||
| + | '''import''' pandas '''as''' pd | ||
| + | '''from''' sklearn.preprocessing '''import''' StandardScaler | ||
| + | |||
| + | '''def''' load_data(data_path): | ||
| + | ds = pd.read_csv(data_path) | ||
| + | y = ds['diagnosis'] | ||
| + | X = ds.drop('diagnosis', axis=1) | ||
| + | X = X.drop('id', axis=1) | ||
| + | i = len(X.columns) | ||
| + | X = X.drop(X.columns[i - 1], axis=1) | ||
| + | y.replace(('M', 'B'), (1, 0), inplace=True) | ||
| + | sc = StandardScaler() | ||
| + | sc.fit(X) | ||
| + | X_ans = sc.transform(X) | ||
| + | return X_ans, y | ||
| + | |||
| + | X, y = load_data("tr.csv") | ||
| + | |||
| + | |||
| + | Теперь <tex>X</tex>, <tex>y</tex> - нормированные значения признаков и соответствуйющие им классы. | ||
* Делим данные на тренировочное и тестовое множество | * Делим данные на тренировочное и тестовое множество | ||
'''from''' sklearn.model_selection '''import''' train_test_split | '''from''' sklearn.model_selection '''import''' train_test_split | ||
| − | X_train, X_validation, y_train, y_validation = train_test_split(X, y, | + | X_train, X_validation, y_train, y_validation = train_test_split(X, y, test_size=0.2, random_state=1234) |
| − | |||
* Создаем классификатор | * Создаем классификатор | ||
| Строка 112: | Строка 135: | ||
'''from''' sklearn.model_selection '''import''' GridSearchCV | '''from''' sklearn.model_selection '''import''' GridSearchCV | ||
| − | + | model_params = best_model.get_params() | |
| + | tuned_params = {} | ||
| + | for k, v in model_params.items(): | ||
| + | tuned_params[k] = [v] | ||
tuned_params['n_neighbors'] = range(1, 30) | tuned_params['n_neighbors'] = range(1, 30) | ||
clf = GridSearchCV(KNeighborsClassifier(), tuned_params, cv=10, n_jobs=-1) | clf = GridSearchCV(KNeighborsClassifier(), tuned_params, cv=10, n_jobs=-1) | ||
| Строка 122: | Строка 148: | ||
best_model = KNeighborsClassifier(**best_params) | best_model = KNeighborsClassifier(**best_params) | ||
| + | best_model.fit(X_train, y_train) | ||
predicted = best_model.predict(X_validation) | predicted = best_model.predict(X_validation) | ||
| Строка 128: | Строка 155: | ||
print('Evaluation:\n', metrics.classification_report(y_validation, predicted)) | print('Evaluation:\n', metrics.classification_report(y_validation, predicted)) | ||
| − | > '''Used params: {'n_neighbors': | + | > '''Used params''': {'metric_params': None, 'metric': 'euclidean', 'weights': 'distance', 'n_neighbors': 9, 'leaf_size': 30, 'n_jobs': 4, 'p': 2, 'algorithm': 'auto'} |
'''Evaluation:''' | '''Evaluation:''' | ||
precision recall f1-score support | precision recall f1-score support | ||
| − | + | 0 0.90 1.00 0.95 69 | |
| − | + | 1 1.00 0.82 0.90 45 | |
| − | + | micro avg 0.93 0.93 0.93 114 | |
| − | + | macro avg 0.95 0.91 0.92 114 | |
| − | + | weighted avg 0.94 0.93 0.93 114 | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | micro avg 0. | ||
| − | macro avg 0. | ||
| − | weighted avg 0. | ||
| − | |||
== См. также == | == См. также == | ||
| Строка 155: | Строка 174: | ||
# [https://en.wikipedia.org/wiki/Kernel_(statistics) Функции ядер] - примеры ядер с Википедии | # [https://en.wikipedia.org/wiki/Kernel_(statistics) Функции ядер] - примеры ядер с Википедии | ||
# [https://scikit-learn.org/stable/modules/generated/sklearn.neighbors.KNeighborsClassifier.html sklearn] - документация по scikit-learn | # [https://scikit-learn.org/stable/modules/generated/sklearn.neighbors.KNeighborsClassifier.html sklearn] - документация по scikit-learn | ||
| + | # [https://www.kaggle.com/jeffbrown/knn-classifier/data kaggle example] - пример по работе с датасетом с kaggle | ||
Версия 23:41, 18 января 2019
Метрический классификатор (англ. similarity-based classifier) — алгоритм классификации, основанный на вычислении оценок сходства между объектами.
Для формализации понятия сходства вводится функция расстояния между объектами . Как правило, не требуется, чтобы были выполнены все три аксиомы метрики - неравенство треугольника может нарушаться.
Метод ближайших соседей — простейший метрический классификатор, основанный на оценивании сходства объектов. Классифицируемый объект относится к тому классу, которому принадлежат ближайшие к нему объекты обучающей выборки.
Метод ближайших соседей (англ. knn - nearest neighbours) — Для повышения надёжности классификации объект относится к тому классу, которому принадлежит большинство из его соседей — ближайших к нему объектов обучающей выборки . В задачах с двумя классами число соседей берут нечётным, чтобы не возникало ситуаций неоднозначности, когда одинаковое число соседей принадлежат разным классам.
Метод взвешенных ближайших соседей — в задачах с числом классов 3 и более нечётность уже не помогает, и ситуации неоднозначности всё равно могут возникать. Тогда -му соседу приписывается вес , как правило, убывающий с ростом ранга соседа . Объект относится к тому классу, который набирает больший суммарный вес среди ближайших соседей.
Содержание
Описание алгоритма
Пусть задана обучающая выборка пар «объект-ответ»
Пусть на множестве объектов задана функция расстояния . Эта функция должна быть достаточно адекватной моделью сходства объектов. Чем больше значение этой функции, тем менее схожими являются два объекта .
Для произвольного объекта расположим объекты обучающей выборки в порядке возрастания расстояний до :
, где через обозначается тот объект обучающей выборки, который является -м соседом объекта . Аналогичное обозначение введём и для ответа на -м соседе: . Таким образом, произвольный объект порождает свою перенумерацию выборки. В наиболее общем виде алгоритм ближайших соседей есть: ,
где — заданная весовая функция, которая оценивает степень важности -го соседа для классификации объекта . Естественно полагать, что эта функция неотрицательна и не возрастает по (поскольку чем дальше объект, тем меньший вклад он должен вносить в пользу своего класса).
По-разному задавая весовую функцию, можно получать различные варианты метода ближайших соседей.
— простейший метод ближайшего соседа;
— метод ближайших соседей;
— метод экспоненциально взвешенных ближайших соседей, где предполагается константа ;
Использование ядер сглаживания
При использовании линейной функции в качестве возможно совпадение суммарного веса для нескольких классов. Это приводит к неоднозначности ответа при классификации. Чтобы такого не происходило используют функцию Ядра[на 15.01.18 не создан].
Будем обозначать функцию ядра
Примеры ядер
Triangular:
Parabolic:
Tricube:
Метод парзеновского окна
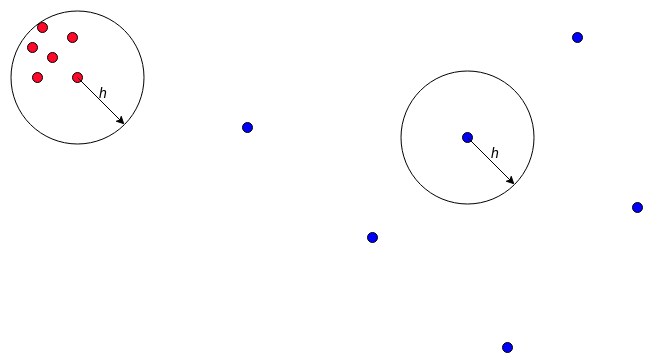
— метод парзеновского окна фиксированной ширины ;
— метод парзеновского окна переменной ширины;
Сравним два этих метода. Сперва запишем классификаторы, полученные при использовании этих методов, в явном виде:
Фиксированной ширины:
Переменной ширины:
не будет учитывать соседей на расстояние больше чем h, а всех остальных учтет в соответствии с функций ядра . является аналогом метода ближайших соседей (т.к. для всех -ых соседей функция вернет 0), но при этом чем ближе -ый сосед, тем больший вклад в сторону своего класса он даст.
Часто используют окно переменной ширины т.е. классификатор , по следующим причинам:
1) Удобнее оптимизировать целочисленный параметр , чем вещественный параметр по некоторой сетке.
2) Существует большое количество задач, где точки разбросаны неравномерно. В них могут существовать области, где достаточно брать небольшую и области, где в окно ширины попадает только одна точка. Тогда для классификатора будут существовать области в которых не будет ни одного объекта (кроме того, который нужно классифицировать). Для таких областей не понятно как классифицировать объекты.
Использование различных метрик расстояния
Очень редко известа хорошая функция расстояния . В качестве нее обычно использую следующие функции:
Примеры метрик
Пусть , - объекты, а , их признаковые описания.
Евклидова метрика:
Расстояние Чебышёва:
Манхэттенское Расстояние:
При их использовании важно нормировать значения признаков, иначе один признак с максимальным значением может стать приобладающим, а признаки с маленькими значениями не будут учитываться при классификации. Чтобы отсеить лишние признаки (т.е. не влияющие на класс объекта) можно использовать feature selection.
Пример использования (через scikit-learn)
Рассмотрим использование алгоритма knn на примере реального датасета. Предположим, что мы загрузили wdbc.data и сохранили как tr.csv с загаловком - описанием признаков.
- Загружаем данные
import pandas as pd from sklearn.preprocessing import StandardScaler
def load_data(data_path):
ds = pd.read_csv(data_path)
y = ds['diagnosis']
X = ds.drop('diagnosis', axis=1)
X = X.drop('id', axis=1)
i = len(X.columns)
X = X.drop(X.columns[i - 1], axis=1)
y.replace(('M', 'B'), (1, 0), inplace=True)
sc = StandardScaler()
sc.fit(X)
X_ans = sc.transform(X)
return X_ans, y
X, y = load_data("tr.csv")
Теперь , - нормированные значения признаков и соответствуйющие им классы.
- Делим данные на тренировочное и тестовое множество
from sklearn.model_selection import train_test_split
X_train, X_validation, y_train, y_validation = train_test_split(X, y, test_size=0.2, random_state=1234)
- Создаем классификатор
from sklearn.neighbors import KNeighborsClassifier
best_model = KNeighborsClassifier( n_neighbors=10, weights=’distance’, algorithm=’auto’, leaf_size=30, metric=’euclidean’, metric_params=None, n_jobs=4 )
- Обучаемся
best_model.fit(X_train, y_train)
- Используем скользящий контроль для поиска лучших параметров (англ. cross validation)
from sklearn.model_selection import GridSearchCV
model_params = best_model.get_params()
tuned_params = {}
for k, v in model_params.items():
tuned_params[k] = [v]
tuned_params['n_neighbors'] = range(1, 30)
clf = GridSearchCV(KNeighborsClassifier(), tuned_params, cv=10, n_jobs=-1)
clf.fit(X_train, y_train)
best_params = clf.best_params_
- Оценка классификатора
from sklearn import metrics
best_model = KNeighborsClassifier(**best_params) best_model.fit(X_train, y_train) predicted = best_model.predict(X_validation)
- Выводим результат
print('Used params:', best_params)
print('Evaluation:\n', metrics.classification_report(y_validation, predicted))
> Used params: {'metric_params': None, 'metric': 'euclidean', 'weights': 'distance', 'n_neighbors': 9, 'leaf_size': 30, 'n_jobs': 4, 'p': 2, 'algorithm': 'auto'}
Evaluation:
precision recall f1-score support
0 0.90 1.00 0.95 69
1 1.00 0.82 0.90 45
micro avg 0.93 0.93 0.93 114
macro avg 0.95 0.91 0.92 114
weighted avg 0.94 0.93 0.93 114
См. также
- Обзор библиотек для машинного обучения на Python[на 30.12.18 не создан]
- Общие понятия[на 30.12.18 не создан]
Источники информации
- Метрический классификатор - статья на machinelearning.ru про метрический классификатор
- knn - статья на machinelearning.ru про knn
- лекция про knn - Лекция из курса К.В. Воронцова
- Функции ядер - примеры ядер с Википедии
- sklearn - документация по scikit-learn
- kaggle example - пример по работе с датасетом с kaggle