Долгая краткосрочная память

Долгая краткосрочная память (англ. Long short-term memory, LSTM) — особая разновидность архитектуры рекуррентных нейронных сетей, способная к обучению долговременным зависимостям, предложенная в 1997 году Сеппом Хохрайтером и Юргеном Шмидхубером.

Описание

Схема слоев долго-краткосрочной памяти

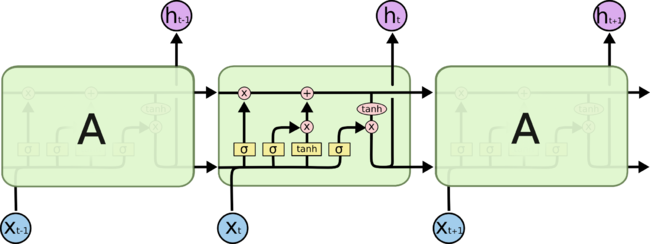
LSTM разработаны специально, чтобы избежать проблемы долговременной зависимости. Запоминание информации на долгие периоды времени — это их обычное поведение. Ключом к данной возможности является то, что LSTM-модуль не использует функцию активации внутри своих рекуррентных компонентов.

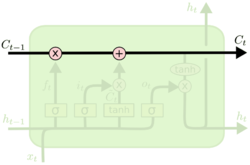
Ключевой компонент LSTM — это состояние ячейки — горизонтальная линия, проходящая по верхней части схемы. Состояние ячейки напоминает конвейерную ленту. Она проходит напрямую через всю цепочку, участвуя лишь в нескольких линейных преобразованиях. Информация может легко течь по ней, не подвергаясь изменениям.

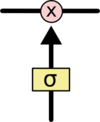
Тем не менее, LSTM может удалять информацию из состояния ячейки; этот процесс регулируется структурами, называемыми фильтрами. Фильтры позволяют пропускать информацию на основании некоторых условий. Они состоят из слоя сигмоидальной нейронной сети и операции поточечного умножения.

Сигмоидальный слой возвращает числа от нуля до единицы, которые обозначают, какую долю каждого блока информации следует пропустить дальше по сети. Ноль в данном случае означает “не пропускать ничего”, единица – “пропустить все”.

Основные компоненты

• Состояние ячейки
• Фильтры, контролирующие состояние ячейки
  • Забывания
  • Входной
  • Выходной

Принцип работы

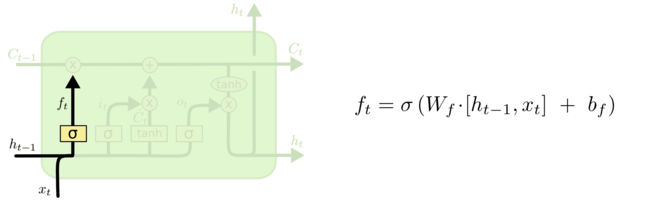
Вначале LSTM определяет, какую информацию можно выбросить из состояния ячейки. Это решение принимает сигмоидальный слой, называемый “слоем фильтра забывания” (англ. forget gate layer). Он смотрит на [math]h_{t-1}[/math] и [math]x_t[/math] и возвращает число от 0 до 1 для каждого числа из состояния ячейки [math]C_t{t-1}[/math] . 1 означает “полностью сохранить”, а 0 – “полностью выбросить”.

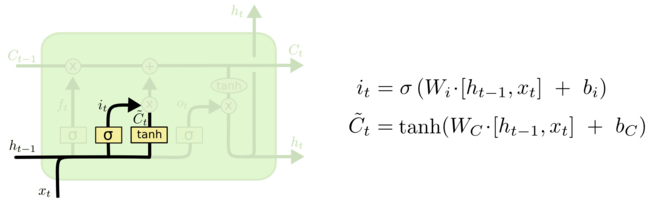
Далее — решается, какая новая информация будет храниться в состоянии ячейки. Этот этап состоит из двух частей. Сначала сигмоидальный слой под названием “слой входного фильтра” (англ. input layer gate) определяет, какие значения следует обновить. Затем tanh-слой строит вектор новых значений-кандидатов [math]\tilde{C}_t[/math], которые можно добавить в состояние ячейки.

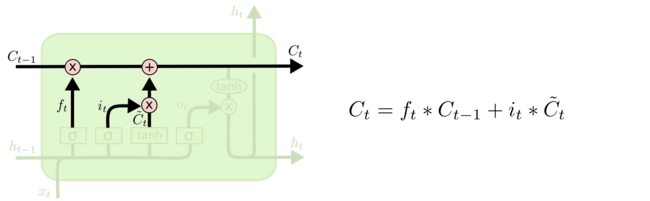
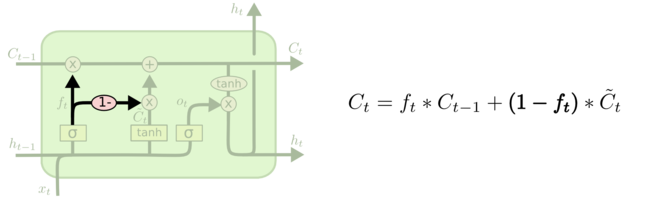
Для замены старого состояния ячейки [math]C_{t-1}[/math] на новое состояние [math]C_t[/math]. Необходимо умножить старое состояние на [math]f_t[/math], забывая то, что мы решили забыть ранее. Затем прибавляем [math]i_t * \tilde{C}_t[/math]. Это новые значения-кандидаты, умноженные на [math]t[/math] – на сколько мы хотим обновить каждое из значений состояния.

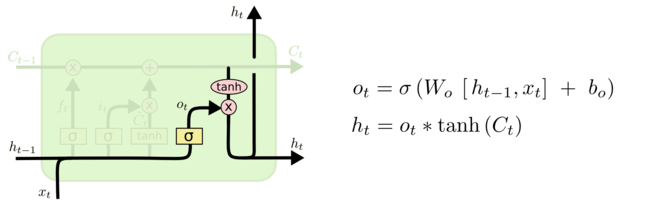
На последнем этапе определяется, то, какую информацию мы хотим получать на выходе. Выходные данные будут основаны на нашем состоянии ячейки, к ним будут применены некоторые фильтры. Сначала мы применяем сигмоидальный слой, который решает, какую информацию из состояния ячейки мы будем выводить. Затем значения состояния ячейки проходят через tanh-слой, чтобы получить на выходе значения из диапазона от -1 до 1, и перемножаются с выходными значениями сигмоидального слоя, что позволяет выводить только требуемую информацию.

Полученные таким образом [math]h_t[/math] и [math]C_t[/math] передаются далее по цепочке.

Вариации

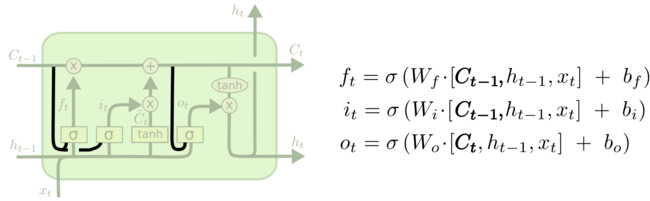
Одна из популярных вариаций LSTM, предложенная Герсом и Шмидхубером, характеризуется добавлением так называемых “смотровых глазков” (“peephole connections”). С их помощью слои фильтров могут видеть состояние ячейки.

На схеме выше “глазки” есть у каждого слоя, но во многих работах они добавляются лишь к некоторым слоям.

Другие модификации включают объединенные фильтры “забывания” и входные фильтры. В этом случае решения, какую информацию следует забыть, а какую запомнить, принимаются не отдельно, а совместно. Мы забываем какую-либо информацию только тогда, когда необходимо записать что-то на ее место. Мы добавляем новую информацию с состояние ячейки только тогда, когда забываем старую.

Немного больше отличаются от стандартных LSTM управляемые рекуррентные нейроны (англ. Gated recurrent units, GRU), впервые описанные в работе Cho. В ней фильтры «забывания» и входа объединяют в один фильтр «обновления» (update gate). Кроме того, состояние ячейки объединяется со скрытым состоянием, есть и другие небольшие изменения. Построенная в результате модель проще, чем стандартная LSTM, и популярность ее неуклонно возрастает.

Существует множество других модификаций, как, например, глубокие управляемые рекуррентные нейронные сети (англ. Depth Gated RNNs), представленные в работе Yao. Есть и другие способы решения проблемы долговременных зависимостей, например, Clockwork RNN Яна Кутника.

Примеры кода

TensorFlow

Пример кода с библиотекой TensorFlow

 # Импорты
 from __future__ import print_function
 import tensorflow as tf
 from tensorflow.contrib import rnn
 
 # Импорт MNIST датасета
 from tensorflow.examples.tutorials.mnist import input_data
 mnist = input_data.read_data_sets("/tmp/data/", one_hot=True)
 
 # Определение параметров обучения
 learning_rate = 0.001
 training_steps = 10000
 batch_size = 128
 display_step = 200
 
 # Определение параметров сети
 num_input = 28
 timesteps = 28
 num_hidden = 128
 num_classes = 10
 
 # Входные данные для графа
 X = tf.placeholder("float", [None, timesteps, num_input])
 Y = tf.placeholder("float", [None, num_classes])
 
 # Определение весов
 weights = {
   'out': tf.Variable(tf.random_normal([num_hidden, num_classes]))
 }
 biases = {
   'out': tf.Variable(tf.random_normal([num_classes]))
 }
 
 def RNN(x, weights, biases):
     x = tf.unstack(x, timesteps, 1)
     # Определение LSTM ячейки
     lstm_cell = rnn.BasicLSTMCell(num_hidden, forget_bias=1.0)
     # Получение выхода LSTM ячейки
     outputs, states = rnn.static_rnn(lstm_cell, x, dtype=tf.float32)
     return tf.matmul(outputs[-1], weights['out']) + biases['out']
 
 logits = RNN(X, weights, biases)
 prediction = tf.nn.softmax(logits)
 
 # Определение функции потерь и оптимизатора
 loss_op = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(
     logits=logits, labels=Y))
 optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate)
 train_op = optimizer.minimize(loss_op)
 
 # Оценка модели
 correct_pred = tf.equal(tf.argmax(prediction, 1), tf.argmax(Y, 1))
 accuracy = tf.reduce_mean(tf.cast(correct_pred, tf.float32))
 
 # Инициализация
 init = tf.global_variables_initializer()
 
 with tf.Session() as sess:
     sess.run(init)
 
     for step in range(1, training_steps+1):
         batch_x, batch_y = mnist.train.next_batch(batch_size)
         batch_x = batch_x.reshape((batch_size, timesteps, num_input))
         # Запуск оптимизатора (обратное распространение ошибки)
         sess.run(train_op, feed_dict={X: batch_x, Y: batch_y})
         if step % display_step == 0 or step == 1:
             loss, acc = sess.run([loss_op, accuracy], feed_dict={X: batch_x, Y: batch_y})
             print("Step " + str(step) + ", Minibatch Loss= " + \
                 "{:.4f}".format(loss) + ", Training Accuracy= " + \
                 "{:.3f}".format(acc))
     print("Optimization Finished!")
 
     test_len = 128
     test_data = mnist.test.images[:test_len].reshape((-1, timesteps, num_input))
     test_label = mnist.test.labels[:test_len]
     print("Testing Accuracy:", \
         sess.run(accuracy, feed_dict={X: test_data, Y: test_label}))

Keras

Пример кода с использованием библиотеки Keras.

 # Импорты
 import numpy as np
 from keras.preprocessing import sequence
 from keras.models import Sequential
 from keras.layers import Dense, Activation, Embedding
 from keras.layers import LSTM
 from keras.datasets import imdb
 
 # Устанавливаем seed для обеспечения повторяемости результатов
 np.random.seed(42)
 
 # Указываем количество слов из частотного словаря, которое будет использоваться (отсортированы по частоте использования)
 max_features = 5000
 
 # Загружаем данные (датасет IMDB содержит 25000 рецензий на фильмы с правильным ответом для обучения и 25000 рецензий на фильмы с правильным ответом для тестирования)
 (X_train, y_train), (X_test, y_test) = imdb.load_data(nb_words = max_features)
 
 # Устанавливаем максимальную длину рецензий в словах, чтобы они все были одной длины
 maxlen = 80
 
 # Заполняем короткие рецензии пробелами, а длинные обрезаем
 X_train = sequence.pad_sequences(X_train, maxlen = maxlen)
 X_test = sequence.pad_sequences(X_test, maxlen = maxlen)
 
 # Создаем модель последовательной сети
 model = Sequential()
 # Добавляем слой для векторного представления слов (5000 слов, каждое представлено вектором из 32 чисел, отключаем входной сигнал с вероятностью 20% для предотвращения переобучения)
 model.add(Embedding(max_features, 32, dropout = 0.2))
 # Добавляем слой долго-краткосрочной памяти (100 элементов для долговременного хранения информации, отключаем входной сигнал с вероятностью 20%, отключаем рекуррентный сигнал с вероятностью 20%)
 model.add(LSTM(100, dropout_W = 0.2, dropout_U = 0.2))
 # Добавляем полносвязный слой из 1 элемента для классификации, в качестве функции активации будем использовать сигмоидальную функцию
 model.add(Dense(1, activation = 'sigmoid'))
 
 # Компилируем модель нейронной сети
 model.compile(loss = 'binary_crossentropy',
               optimizer = 'adam',
               metrics = ['accuracy'])
 
 # Обучаем нейронную сеть (данные для обучения, ответы к данным для обучения, количество рецензий после анализа которого будут изменены веса, число эпох обучения, тестовые данные, показывать progress bar или нет)
 model.fit(X_train, y_train, 
           batch_size = 64,
           nb_epoch = 7,
           validation_data = (X_test, y_test),
           verbose = 1)
 
 # Проверяем качество обучения на тестовых данных (если есть данные, которые не участвовали в обучении, лучше использовать их, но в нашем случае таковых нет)
 scores = model.evaluate(X_test, y_test, batch_size = 64)
 print('Точность на тестовых данных: %.2f%%' % (scores[1] * 100))

См. также

• Рекуррентные нейронные сети
• Нейронные сети, перцептрон
• Сверточные нейронные сети
• Рекурсивные нейронные сети