Байесовские сети — различия между версиями
| Строка 13: | Строка 13: | ||
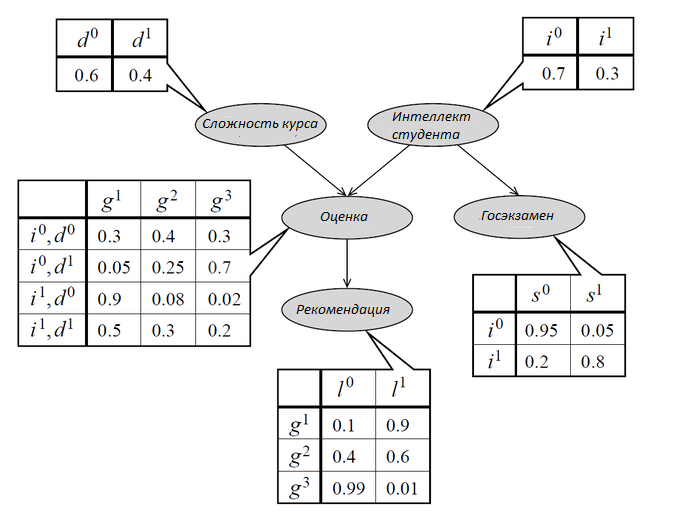
С помощью цепного правила рассчитаем вероятность того, что умный студент получает B по лёгкому курсу, высокий балл по SAT и плохое рекомендательное письмо: <math> P(i1, d0, g2, s1, l0) = P(i1)P(d0)P(g2 | i1, d0)P(s1 | i1)P(l0 | g2) = 0.3*0.6*0.08*0.8*0.4 = 0.004608. </math> | С помощью цепного правила рассчитаем вероятность того, что умный студент получает B по лёгкому курсу, высокий балл по SAT и плохое рекомендательное письмо: <math> P(i1, d0, g2, s1, l0) = P(i1)P(d0)P(g2 | i1, d0)P(s1 | i1)P(l0 | g2) = 0.3*0.6*0.08*0.8*0.4 = 0.004608. </math> | ||
| + | |||
| + | Байесовская сеть представляет законное распределение: | ||
| + | * Вероятность исхода в Байесовской сети неотрицательна, так как вычисляется как произведение условных вероятностей событий, которые неотрицательны. | ||
| + | * Сумма вероятностей исходов в Байесовской сети равна единице: | ||
| + | |||
| + | <math>\sum\limits_{D,I,G,S,L} P(D,I,G,S,L) = \sum\limits_{D,I,G,S,L} P(D)P(I)P(G|I,D)P(S|I)P(L|G) = \sum\limits_{D,I,G,S} P(D)P(I)P(G|I,D)P(S|I) \sum\limits_{L} P(L|G) = \sum\limits_{D,I,G,S} P(D)P(I)P(G|I,D)P(S|I) = </math> | ||
| + | |||
| + | <math>\sum\limits_{D,I,G} P(D)P(I)P(G|I,D) \sum\limits_{S} P(S|I) = \sum\limits_{D,I,G} P(D)P(I)P(G|I,D) = ... </math> | ||
== Источники информации == | == Источники информации == | ||
* Andrew D. Gordon, Thomas A. Henzinger, Aditya V. Nori, and Sriram K. Rajamani. 2014. Probabilistic programming. In Proceedings of the on Future of Software Engineering (FOSE 2014). ACM, New York, NY, USA, 167-181. DOI=10.1145/2593882.2593900 doi.acm.org/10.1145/2593882.2593900 | * Andrew D. Gordon, Thomas A. Henzinger, Aditya V. Nori, and Sriram K. Rajamani. 2014. Probabilistic programming. In Proceedings of the on Future of Software Engineering (FOSE 2014). ACM, New York, NY, USA, 167-181. DOI=10.1145/2593882.2593900 doi.acm.org/10.1145/2593882.2593900 | ||
Версия 23:30, 9 марта 2019
| Определение: |
| Байесовская сеть (англ. Bayesian network) — это направленный ациклический граф , в котором каждой вершине поставлена в соответствие случайная переменная и каждое ребро представляет прямую зависимость от . Пусть , тогда в Байесовской сети каждой вершине графа должно быть сопоставлено распределение условных вероятностей от вершин из . |
Цепное правило для Байесовских сетей:
Пример
Оценка студента (Grade) зависит от его интеллекта (Intelligence) и сложности курса (Difficulty). Студент просит у преподавателя рекомендательное письмо (Letter), предположим, что преподаватель может написать плохое или хорошее письмо в зависимости от оценки студента. Также студент сдаёт экзамен для поступления в колледж (SAT), результаты экзамена не зависят от письма преподавателя, оценки за его курс и сложности курса. Представление этой модели в Байесовской сети представлено на рисунке ниже.
С помощью цепного правила рассчитаем вероятность того, что умный студент получает B по лёгкому курсу, высокий балл по SAT и плохое рекомендательное письмо:
Байесовская сеть представляет законное распределение:
- Вероятность исхода в Байесовской сети неотрицательна, так как вычисляется как произведение условных вероятностей событий, которые неотрицательны.
- Сумма вероятностей исходов в Байесовской сети равна единице:
Источники информации
- Andrew D. Gordon, Thomas A. Henzinger, Aditya V. Nori, and Sriram K. Rajamani. 2014. Probabilistic programming. In Proceedings of the on Future of Software Engineering (FOSE 2014). ACM, New York, NY, USA, 167-181. DOI=10.1145/2593882.2593900 doi.acm.org/10.1145/2593882.2593900