Алгоритм Лампорта взаимного исключения — различия между версиями
Yeputons (обсуждение | вклад) |
|||
| Строка 1: | Строка 1: | ||
[[Категория: Параллельное программирование]] | [[Категория: Параллельное программирование]] | ||
| − | '''Алгоритм Лампорта''' -- алгоритм взаимного исключения, работающий в случае, если все сообщения идут FIFO и использующий логические часы Лампорта. | + | '''Алгоритм Лампорта''' -- алгоритм взаимного исключения, работающий в случае, если все сообщения идут FIFO и использующий [[логические часы Лампорта]] (т.е. с каждым сообщением посылается ещё и временна́я метка). |
Каждый поток поддерживает очередь запросов на вход в критическую секцию. Приоритет – <временная метка, номер потока> (т.е при равенстве временных меток берем тот поток, чей номер меньше). | Каждый поток поддерживает очередь запросов на вход в критическую секцию. Приоритет – <временная метка, номер потока> (т.е при равенстве временных меток берем тот поток, чей номер меньше). | ||
| − | Когда поток хочет войти в критическую секцию, он: | + | Когда поток хочет войти в критическую секцию, он: |
# Добавляет свой запрос в свою очередь (т.е временную метку и номер потока) | # Добавляет свой запрос в свою очередь (т.е временную метку и номер потока) | ||
# Посылает всем потокам запрос (req) | # Посылает всем потокам запрос (req) | ||
| Строка 16: | Строка 16: | ||
Суммарно на каждую критическую секцию приходится <tex>3(N - 1)</tex> сообщение. | Суммарно на каждую критическую секцию приходится <tex>3(N - 1)</tex> сообщение. | ||
| + | |||
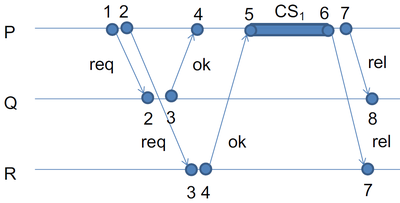
| + | [[Файл:mutex-distributed-lamport.png|400px]] | ||
| + | |||
| + | Корректность гарантируется при помощи FIFO и ok: если $P$ получил ok от процесса $Q$, то запрос от $Q$ на вход в критическую секцию уже тоже получен. | ||
| + | |||
| + | ''Неаккуратное'' доказательство: если $P$ и $Q$ решили одновременно войти в критическую секцию, то они оба получили друг от друга ok и, следовательно, знают друг про друга. А тогда $P$ не может быть минимальным в очереди $P$, а $Q$ — минимальным в очереди $Q$. | ||
| + | Намёки, почему неаккуратно: | ||
| + | |||
| + | # Используется запретное слово "одновременно", а не "произошло-до". | ||
| + | # Нигде нет отсылок к тому, что мы используем логические часы в качестве меток, а не просто случайные числа. | ||
| + | |||
| + | Чуть более аккуратное доказательство не требуется на экзамене, но есть в книжке Gaarg, страницы 24 и 26 (впрочем, там тоже есть "одновременно", но уже не так явно). | ||
| + | Пусть процесс $P_i$ в момент времени $e'$ выбрал для захода в критическую секцию метку $x_i$ ($C(e')=x_i$) и зашёл в неё в момент времени $e$, | ||
| + | а процесс $P_k$ в момент времени $f'$ выбрал метку $x_k$ ($C(f)=x_k$). | ||
| + | Раз $P_i$ зашёл в секцию, то он, в частности, получил подтверждение от $P_k$. Процесс $P_k$ отправил его в момент $g$ (''сразу'' после получения запроса на подтверждение). Два случая: | ||
| + | |||
| + | # Если $g < f$ (т.е. $P_k$ решил входить в секцию после того, как узнал про $P_i$), то $x_i = C(e') < C(g) < C(f) = x_k$. То есть процесс $P_k$ знает про $P_i$ и имеет строго больший номер. Тогда он может зайти в критическую секцию только после выхода $P_i$ из секции и получения об этом сообщения, то есть его вход происходит-после выхода $P_i$. | ||
| + | # Если $f < g$, то процесс $P_i$ получит от $P_k$ сообщение req до того, как получит подтверждение в момент $g$. Таким образом, оба потока знают друг про друга. И раз $P_i$ решил входить в секцию, то либо он уже знает, что $P_k$ вошёл в секцию (при помощи сообщений), либо у него номер строго меньше (тогда $P_k$ не будет входить в секцию, пока $P_i$ не выйдет). | ||
Версия 18:25, 2 июня 2019
Алгоритм Лампорта -- алгоритм взаимного исключения, работающий в случае, если все сообщения идут FIFO и использующий логические часы Лампорта (т.е. с каждым сообщением посылается ещё и временна́я метка).
Каждый поток поддерживает очередь запросов на вход в критическую секцию. Приоритет – <временная метка, номер потока> (т.е при равенстве временных меток берем тот поток, чей номер меньше).
Когда поток хочет войти в критическую секцию, он:
- Добавляет свой запрос в свою очередь (т.е временную метку и номер потока)
- Посылает всем потокам запрос (req)
- Ждет от них ответа (ok)
- Получив все ответы, ждет, когда он станет первым в своей очереди, и входит в критическую секцию
- Выйдя из критической секции, удаляет свой запрос из своей очереди, посылает всем сообщение о том, что вышел (rel)
Действия вне критической секции:
- При получении запроса от другого потока, запрос добавляется в очередь и запрашивающему потоку посылается ответ
- При получении release от другого потока, его запрос удаляется из очереди
Суммарно на каждую критическую секцию приходится сообщение.
Корректность гарантируется при помощи FIFO и ok: если $P$ получил ok от процесса $Q$, то запрос от $Q$ на вход в критическую секцию уже тоже получен.
Неаккуратное доказательство: если $P$ и $Q$ решили одновременно войти в критическую секцию, то они оба получили друг от друга ok и, следовательно, знают друг про друга. А тогда $P$ не может быть минимальным в очереди $P$, а $Q$ — минимальным в очереди $Q$. Намёки, почему неаккуратно:
- Используется запретное слово "одновременно", а не "произошло-до".
- Нигде нет отсылок к тому, что мы используем логические часы в качестве меток, а не просто случайные числа.
Чуть более аккуратное доказательство не требуется на экзамене, но есть в книжке Gaarg, страницы 24 и 26 (впрочем, там тоже есть "одновременно", но уже не так явно). Пусть процесс $P_i$ в момент времени $e'$ выбрал для захода в критическую секцию метку $x_i$ ($C(e')=x_i$) и зашёл в неё в момент времени $e$, а процесс $P_k$ в момент времени $f'$ выбрал метку $x_k$ ($C(f)=x_k$). Раз $P_i$ зашёл в секцию, то он, в частности, получил подтверждение от $P_k$. Процесс $P_k$ отправил его в момент $g$ (сразу после получения запроса на подтверждение). Два случая:
- Если $g < f$ (т.е. $P_k$ решил входить в секцию после того, как узнал про $P_i$), то $x_i = C(e') < C(g) < C(f) = x_k$. То есть процесс $P_k$ знает про $P_i$ и имеет строго больший номер. Тогда он может зайти в критическую секцию только после выхода $P_i$ из секции и получения об этом сообщения, то есть его вход происходит-после выхода $P_i$.
- Если $f < g$, то процесс $P_i$ получит от $P_k$ сообщение req до того, как получит подтверждение в момент $g$. Таким образом, оба потока знают друг про друга. И раз $P_i$ решил входить в секцию, то либо он уже знает, что $P_k$ вошёл в секцию (при помощи сообщений), либо у него номер строго меньше (тогда $P_k$ не будет входить в секцию, пока $P_i$ не выйдет).