Теорема Понтрягина-Куратовского — различия между версиями
м ("Внутрення" заменено на "внутренняя".) |
|||
| Строка 1: | Строка 1: | ||
| + | {| class="wikitable" align="center" style="color: red; background-color: black; font-size: 56px; width: 800px;" | ||
| + | |+ | ||
| + | |-align="center" | ||
| + | |'''НЕТ ВОЙНЕ''' | ||
| + | |-style="font-size: 16px;" | ||
| + | | | ||
| + | 24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян. | ||
| + | |||
| + | Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием. | ||
| + | |||
| + | Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей. | ||
| + | |||
| + | Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить. | ||
| + | |||
| + | ''Антивоенный комитет России'' | ||
| + | |-style="font-size: 16px;" | ||
| + | |Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению. | ||
| + | |-style="font-size: 16px;" | ||
| + | |[https://meduza.io/ meduza.io], [https://www.youtube.com/c/popularpolitics/videos Популярная политика], [https://novayagazeta.ru/ Новая газета], [https://zona.media/ zona.media], [https://www.youtube.com/c/MackNack/videos Майкл Наки]. | ||
| + | |} | ||
| + | |||
Теорему доказал в 1927 году известный советский математик Лев Семенович Понтрягин, но не опубликовал. | Теорему доказал в 1927 году известный советский математик Лев Семенович Понтрягин, но не опубликовал. | ||
Независимо от Понтрягина в 1930 году доказательста нашел и впервые напечатал польский математик Казимир Куратовский. | Независимо от Понтрягина в 1930 году доказательста нашел и впервые напечатал польский математик Казимир Куратовский. | ||
Версия 06:53, 1 сентября 2022
| НЕТ ВОЙНЕ |
|
24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян. Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием. Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей. Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить. Антивоенный комитет России |
| Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению. |
| meduza.io, Популярная политика, Новая газета, zona.media, Майкл Наки. |
Теорему доказал в 1927 году известный советский математик Лев Семенович Понтрягин, но не опубликовал.
Независимо от Понтрягина в 1930 году доказательста нашел и впервые напечатал польский математик Казимир Куратовский.
Первые доказательства теоремы Понтрягина-Куратовского были очень сложными. Сравнительно простое доказательство нашел в 1997 г. петербургский школьник Юрий Макарычев.
Содержание
- 1 G связен
- 2 G — обыкновенный граф
- 3 G — блок
- 4 В G нет мостов
- 5 В G' существует цикл, содержащий вершины a и b
- 6 Вспомогательные определения и утверждение об одновременно разделяющейся внутренней части
- 7 Разбор случаев взаимного положения вершин a, b, c, d, u1, u2, v1, v2
- 8 См. также
- 9 Примечания
- 10 Источники информации
| Теорема: | ||||||||||||||||||||||||||
Граф планарен тогда и только тогда, когда он не содержит подграфов, гомеоморфных или . | ||||||||||||||||||||||||||
| Доказательство: | ||||||||||||||||||||||||||
|
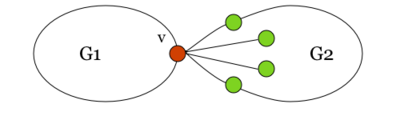
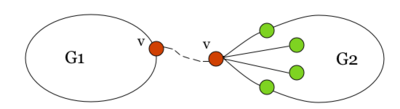
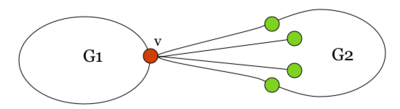
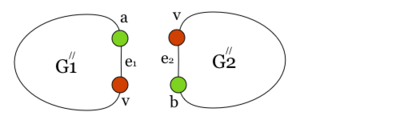
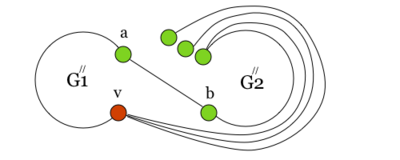
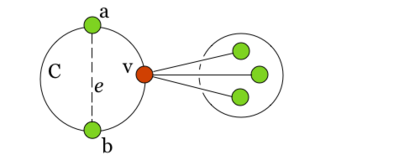
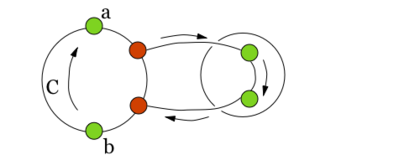
Заметим, что из планарности графа следует планарность гомеоморфного графа и наоборот. В самом деле, пусть — плоский граф. Если добавить на нужных ребрах вершины степени и удалить некотрые вершины степени в , получим укладку гомеоморфного графа . Таким образом, доказательство необходимости следует из непланарности и . Докажем достаточность. От противного: пусть существует непланарный граф, который не содержит подграфов, гомеоморфных или . Пусть — такой граф с наименьшим возможным числом рёбер, не содержащий изолированных вершин. G связенЕсли не связен, то в силу минимальности его компоненты связности планарны и, следовательно, сам граф планарен. G — обыкновенный графВ самом деле, пусть в графе есть петля или кратное ребро . Тогда в силу минимальности граф планарен. Добавляя ребро к графу получим, что граф планарен. G — блокПусть, от противного, в графе есть точка сочленения . Через обозначим подграф графа , порождённый вершинами одной из компонент связности графа и вершинной , а через подграф графа , порождённый вершинами остальных компонент связности графа и вершиной . В силу минимальности , и — планарны. Возьмём укладку графа на плоскости такую, что вершина лежит на границе внешней грани. Ее можно получить, взяв любую укладку на плоскости, по ней построив укладку на шаре, используя обратную стереографическую проекцию[1], потом повернуть сферу так, чтоб оказалась на внешней грани стереографической проекции повернутого шара. Затем во внешней грани графа возьмём укладку графа такую, что вершина будет представлена на плоскости в двух экземплярах. Соединим два экземпляра вершины пучком жордановых линий, не допуская лишних пересечений с укладками графов и , состоящим из такого количества линий, какова степень вершины в графе . Далее отбросим вхождение вершины в граф , заменяя инцидентные ей рёбра на жордановы линии, полученные из линий указанного пучка и рёбер. Таким образом мы получили укладку графа на плоскости, что невозможно. В G нет мостовГраф не равен и в нем нет точек сочленения, следовательно в нет мостов. В G' существует цикл, содержащий вершины a и bПусть — произвольное ребро графа , .
Пусть и лежат в одном блоке графа .
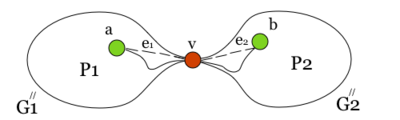
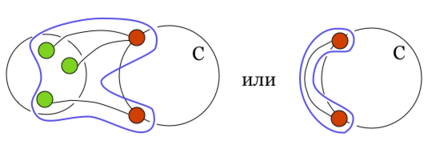
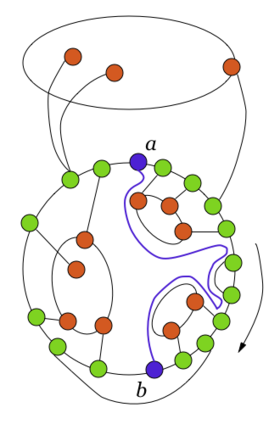
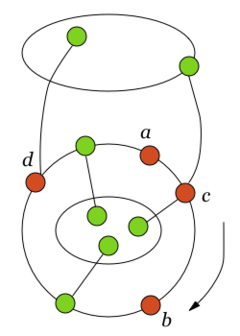
Заметим, что в графе рёбер меньше, чем в графе . Действительно, вместо ребра в есть ребро и часть рёбер из графа осталась в графе . Аналогично, в графе рёбер меньше, чем в графе . Отметим, что опять вершина представлена на плоскости в двух экземплярах. Очевидно, добавление ребра не меняет планарности графа . Склеим оба вхождения вершины точно так же, как это мы сделали в предыдущем пункте доказательства. Сотрем затем ранее добавленные ребра и . В результате мы получим укладку графа на плоскости, что невозможно. Утверждение доказано. Вспомогательные определения и утверждение об одновременно разделяющейся внутренней частиСреди всех укладок графа на плоскости и среди всех циклов , содержащих и , зафиксируем такую укладку и такой цикл, что внутри области, ограниченной циклом , лежит максимальное возможное число граней графа . Зафиксируем один из обходов по циклу (на рисунках будем рассматривать обход по часовой стрелке по циклу ). Для вершин и цикла через будем обозначать простую — цепь, идущую по циклу от до в направлении обхода цикла. Конечно, . Положим {}, т.е. получено из отбрасыванием вершин и .
В силу связности графа для любой внешней компоненты должны существовать рёбра в , соединяющие её с вершинами цикла .
В силу связности графа для любой внутренней компоненты должны существовать рёбра в , соединяющие её с вершинами цикла .
Будем говорить, что внешняя (внутренняя) часть встречает цикл в своих точках прикрепления к циклу .
Аналогично можно ввести понятие — разделяющей внутренней части. Заметим, что внутренняя часть может встречать цикл , вообще говоря, более чем в двух точках, но не менее чем в двух точках.
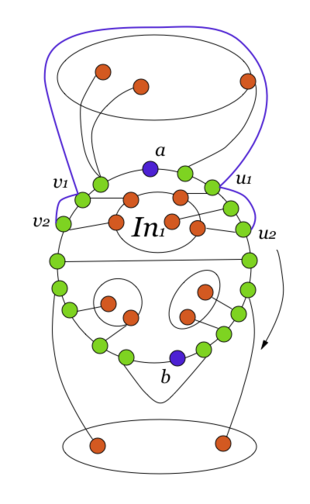
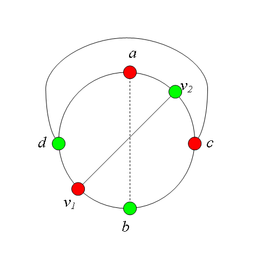
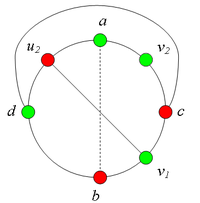
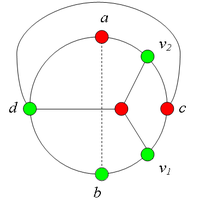
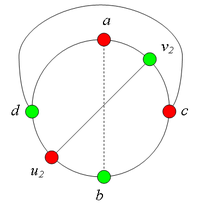
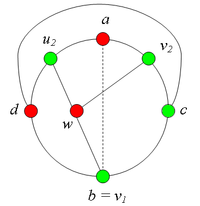
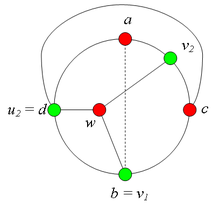
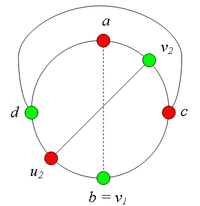
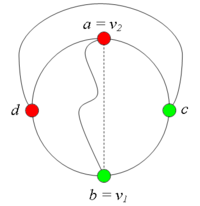
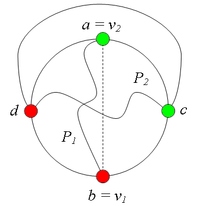
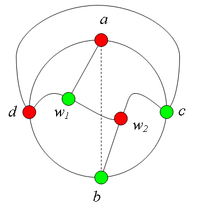
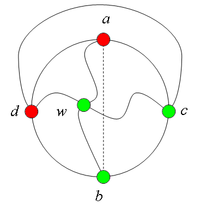
Разбор случаев взаимного положения вершин a, b, c, d, u1, u2, v1, v2
| ||||||||||||||||||||||||||
См. также
Примечания
Источники информации
- Википедия — Планарный граф
- Wikipedia — Kuratowski's theorem
- "Вокруг критерия Куратовского планарности графов" (стр. 118)
- Асанов М., Баранский В., Расин В. — Дискретная математика — Графы, матроиды, алгоритмы