Регуляризация — различия между версиями
(→Мотивация) |
|||
| Строка 5: | Строка 5: | ||
==Мотивация== | ==Мотивация== | ||
| + | Как говорилось ранее, регуляризация полезна для борьбы с <переобучением>. Если вы выбрали сложную модель, и при этом у вас недостаточно данных, то легко можно получить итоговую модель, которая хорошо описывает обучающую выборку, но не обобщается на тестовую. | ||
| + | |||
| + | В качестве наглядного примера можно рассмотреть линейные регрессионные модели. | ||
| + | Восстановить зависимость для нескольких точек можно пытаться полиномами разной степени. | ||
| + | |||
| + | {|align="center" | ||
| + | |-valign="top" | ||
| + | |[[Файл:High_bias_reg.png|200px|thumb|Рис 1. Недообучение. M=1]] | ||
| + | |[[Файл:Normal_bias_reg.png|200px|thumb|Рис 2. Норма. M=2]] | ||
| + | |[[Файл:High_variance_reg.png|200px|thumb|Рис 3. Переобучение. M=4]] | ||
| + | |} | ||
==Основные виды регуляризации== | ==Основные виды регуляризации== | ||
Версия 03:10, 19 января 2020
| Определение: |
| Регуляризация (англ. regularization) в статистике, машинном обучении, теории обратных задач — метод добавления некоторых дополнительных ограничений к условию с целью решить неккоректно поставленную задачу или предотвратить переобучение. Чаще всего эта информация имеет вид штрафа за сложность модели. |
Содержание
Мотивация
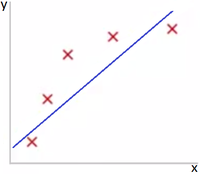
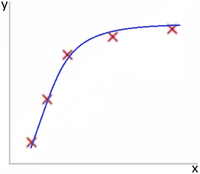
Как говорилось ранее, регуляризация полезна для борьбы с <переобучением>. Если вы выбрали сложную модель, и при этом у вас недостаточно данных, то легко можно получить итоговую модель, которая хорошо описывает обучающую выборку, но не обобщается на тестовую.
В качестве наглядного примера можно рассмотреть линейные регрессионные модели. Восстановить зависимость для нескольких точек можно пытаться полиномами разной степени.