Графовые нейронные сети — различия между версиями
Glosus (обсуждение | вклад) (→Графовые нейронные сети: Описание) |
Glosus (обсуждение | вклад) (Release version 1.0) |
||
| Строка 1: | Строка 1: | ||
| + | [[Файл:GnnGraph.png|thumb|250px|Граф]] | ||
| + | |||
| + | '''Графовая нейронная сеть''' (англ. Graph Neural Network, GNN) – тип нейронной сети, которая напрямую работает со структурой графа. Типичным применением GNN является классификация узлов. Концепция графовой нейронной сети была впервые предложена в 2009 году в работе <ref>[https://ro.uow.edu.au/infopapers/3165/ The graph neural network model, University of Wollongong Australia]</ref>, которая расширила существующие нейронные сети для обработки данных, представленных в графовых областях. | ||
| + | |||
| + | == Идея == | ||
| − | |||
| − | |||
При работе с естественными языками, обработке и анализе изображений, построении моделей веб-сетей и еще широком спектре прикладных задач, бывает удобно представлять данные в виде графов. Однако для традиционных методов машинного обучения необходимо предварительно преобразовывать графово структурированные данные в другие структуры данных, к примеру числовой вектор. Такой подход может привести к потере части информации, заключающейся во взаиморасположении узлов сети. | При работе с естественными языками, обработке и анализе изображений, построении моделей веб-сетей и еще широком спектре прикладных задач, бывает удобно представлять данные в виде графов. Однако для традиционных методов машинного обучения необходимо предварительно преобразовывать графово структурированные данные в другие структуры данных, к примеру числовой вектор. Такой подход может привести к потере части информации, заключающейся во взаиморасположении узлов сети. | ||
| + | {{Определение | ||
| + | |definition= | ||
| + | Граф – это структура данных, состоящая из двух компонентов: вершин и ребер. Граф G описывается множеством вершин (узлов) V и ребер E, которые он содержит <tex>G = (V,E)</tex>. | ||
| + | }} | ||
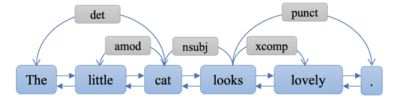
| + | [[Файл:TextGNN.PNG|thumb|400px|Пример графа для анализа текста.]] | ||
| + | GNN позволяет обрабатывать графово структурированную информацию без стадии предварительной обработки, сохраняя таким образом топологические отношения между узлами графа. Графовые нейронные сети основаны на механизме распространения информации, т.е. граф обрабатывается набором модулей, каждый из которых связан с узлом графа. В свою очередь модули связаны в соответствии со связями графа. Модули обновляют свое состояние и обмениваются информацией до тех пор, пока не достигнут устойчивого равновесия. Выходные данные GNN вычисляются в каждом узле на основе состояния модуля. Механизм распространения ограничен, чтобы гарантировать, что уникальное устойчивое состояние всегда существует. | ||
| + | |||
| + | В последние годы системы, основанные на вариантах графовых нейронных сетей, таких как graph convolutional network (GCN), graph attention network (GAT), gated graph neural network (GGNN), продемонстрировали высокую производительность при решении многих задач, обозначенных выше. | ||
| + | |||
| + | {|align="center" | ||
| + | |-valign="top" | ||
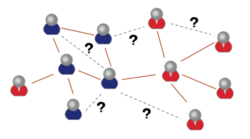
| + | |[[Файл:Social_network.PNG|250px|thumb|Социальные сети]] | ||
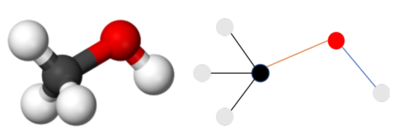
| + | |[[Файл:MoleculeGNN.PNG|400px|thumb|Молекулы]] | ||
| + | |[[Файл:ImageGNN.PNG|312px|thumb|Изображения]] | ||
| + | |} | ||
| − | + | == Описание == | |
В графе каждый узел определяется его признаками и связанными узлами. Целью GNN является изучение состояния встраивания <tex>h_v \in R^{S}</tex>, которое содержит информацию об окрестностях для каждого узла. Состояние встраивания <tex>h_v</tex> - это s-мерный вектор из вершины <tex>v</tex>, который может быть использован для получения выхода <tex>O_v</tex> (метки узла). | В графе каждый узел определяется его признаками и связанными узлами. Целью GNN является изучение состояния встраивания <tex>h_v \in R^{S}</tex>, которое содержит информацию об окрестностях для каждого узла. Состояние встраивания <tex>h_v</tex> - это s-мерный вектор из вершины <tex>v</tex>, который может быть использован для получения выхода <tex>O_v</tex> (метки узла). | ||
| Строка 10: | Строка 28: | ||
Пусть <tex>f</tex> - это параметрическая функция, называемая ''локальной переходной функцией'', которая является общей для всех узлов и обновляет состояние узла в соответствии с входной окрестностью. Также пусть <tex>g</tex> - ''локальная выходная функция'', которая описывает, как выход был производен. Тогда <tex>h_v</tex> и <tex>o_v</tex> определяются следующим образом: | Пусть <tex>f</tex> - это параметрическая функция, называемая ''локальной переходной функцией'', которая является общей для всех узлов и обновляет состояние узла в соответствии с входной окрестностью. Также пусть <tex>g</tex> - ''локальная выходная функция'', которая описывает, как выход был производен. Тогда <tex>h_v</tex> и <tex>o_v</tex> определяются следующим образом: | ||
| − | <tex>h_v = f{(x_v, x_{co[v]}, h_{ne[v]}, x_{ne[v]})}</tex> | + | <center><tex>h_v = f{(x_v, x_{co[v]}, h_{ne[v]}, x_{ne[v]})}</tex></center> |
| − | <tex>o_v = g{(h_v,X_v)}</tex> | + | <center><tex>o_v = g{(h_v,X_v)}</tex></center> |
где <tex>x_v, x_{co[v]}, h_{ne[v]}, x_{ne[v]}</tex> являются признаками <tex>v</tex>, признаками его ребер, состояний, и признаками узлов в окрестностях <tex>v</tex> соответственно. | где <tex>x_v, x_{co[v]}, h_{ne[v]}, x_{ne[v]}</tex> являются признаками <tex>v</tex>, признаками его ребер, состояний, и признаками узлов в окрестностях <tex>v</tex> соответственно. | ||
| Строка 18: | Строка 36: | ||
Пусть <tex>H, O, X</tex> и <tex>X_N</tex> - это векторы, построенные путем укладки всех состояний, всех выходных данных, всех признаков и всех признаков узлов соответственно. Тогда мы можем представить уравнения в более компактной форме: | Пусть <tex>H, O, X</tex> и <tex>X_N</tex> - это векторы, построенные путем укладки всех состояний, всех выходных данных, всех признаков и всех признаков узлов соответственно. Тогда мы можем представить уравнения в более компактной форме: | ||
| − | <tex>H = F{(H,X)}</tex> | + | <center><tex>H = F{(H,X)}</tex></center> |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <center><tex>O = G{(H,X_N)}</tex></center> | |
| − | <tex> | + | где <tex>F</tex> - это ''глобальная функция перехода'', а <tex>G</tex> - ''глобальная выходная функция'', которая является сложенной версией <tex>f</tex> и <tex>g</tex> для всех узлов в графе соответственно. Значение <tex>H</tex> является фиксированным и однозначно определяется в предположением о том, что <tex>F</tex> - это карта сжатия. |
| − | где <tex>H^t</tex> обозначает <tex>t</tex>-ую итерацию <tex>H</tex>. Динамическая система из этого уравнения сходится экспоненциально быстро к решению уравнения <tex>H = F{(H,X)}</tex> для любого начального значения <tex>H(0)</tex>. Стоит отметить, что вычисления описанные в <tex>f</tex> и <tex>g</tex>, могут быть интерпретированы как нейронные сети с прямой связью. | + | С учетом теоремы Банаха о неподвижной точке GNN использует следующую классическую итерационную схему для вычисления состояния: <tex>H^{t+1} = F{(H^t,X)}</tex>, где <tex>H^t</tex> обозначает <tex>t</tex>-ую итерацию <tex>H</tex>. Динамическая система из этого уравнения сходится экспоненциально быстро к решению уравнения <tex>H = F{(H,X)}</tex> для любого начального значения <tex>H(0)</tex>. Стоит отметить, что вычисления описанные в <tex>f</tex> и <tex>g</tex>, могут быть интерпретированы как нейронные сети с прямой связью. |
Следующие задачей становится поиск параметров <tex>f</tex> и <tex>g</tex>. С помощью целевой информации (<tex>t_v</tex> для конкретного узла) для контроля, функция потерь может быть вычислена следующим образом: | Следующие задачей становится поиск параметров <tex>f</tex> и <tex>g</tex>. С помощью целевой информации (<tex>t_v</tex> для конкретного узла) для контроля, функция потерь может быть вычислена следующим образом: | ||
| − | <tex>loss = \sum_{i=1}^{p}{(t_i-o_i)}</tex> | + | <center><tex>loss = \sum_{i=1}^{p}{(t_i-o_i)}</tex></center> |
где <tex>p</tex> - это число контролируемых узлов. Алгоритм обучения основан на стратегии градиентного спуска и состоит из следующих шагов: | где <tex>p</tex> - это число контролируемых узлов. Алгоритм обучения основан на стратегии градиентного спуска и состоит из следующих шагов: | ||
| Строка 51: | Строка 65: | ||
Наконец, нецелесообразно использовать фиксированные точки, если мы сосредоточимся на представлении узлов вместо графиков, поскольку распределение представления в фиксированной точке будет гораздо более гладким по значению и менее информативным для различения каждого узла. | Наконец, нецелесообразно использовать фиксированные точки, если мы сосредоточимся на представлении узлов вместо графиков, поскольку распределение представления в фиксированной точке будет гораздо более гладким по значению и менее информативным для различения каждого узла. | ||
| + | |||
| + | == Примечания == | ||
| + | <references/> | ||
| + | |||
| + | == Источники информации== | ||
| + | * [https://ieeexplore.ieee.org/document/4700287 The Graph Neural Network Model] | ||
| + | * [https://arxiv.org/pdf/1812.08434.pdf Graph Neural Networks: A Review of Methods and Applications] | ||
| + | * [https://towardsdatascience.com/a-gentle-introduction-to-graph-neural-network-basics-deepwalk-and-graphsage-db5d540d50b3 A Gentle Introduction to Graph Neural Networks (Basics, DeepWalk, and GraphSage)] | ||
| + | * [https://towardsdatascience.com/hands-on-graph-neural-networks-with-pytorch-pytorch-geometric-359487e221a8 Hands-on Graph Neural Networks with PyTorch & PyTorch Geometric] | ||
| + | * [https://cyberleninka.ru/article/n/grafovye-neyronnye-seti Графовые нейронные сети] | ||
Версия 01:56, 18 марта 2020
Графовая нейронная сеть (англ. Graph Neural Network, GNN) – тип нейронной сети, которая напрямую работает со структурой графа. Типичным применением GNN является классификация узлов. Концепция графовой нейронной сети была впервые предложена в 2009 году в работе [1], которая расширила существующие нейронные сети для обработки данных, представленных в графовых областях.
Идея
При работе с естественными языками, обработке и анализе изображений, построении моделей веб-сетей и еще широком спектре прикладных задач, бывает удобно представлять данные в виде графов. Однако для традиционных методов машинного обучения необходимо предварительно преобразовывать графово структурированные данные в другие структуры данных, к примеру числовой вектор. Такой подход может привести к потере части информации, заключающейся во взаиморасположении узлов сети.
| Определение: |
| Граф – это структура данных, состоящая из двух компонентов: вершин и ребер. Граф G описывается множеством вершин (узлов) V и ребер E, которые он содержит . |
GNN позволяет обрабатывать графово структурированную информацию без стадии предварительной обработки, сохраняя таким образом топологические отношения между узлами графа. Графовые нейронные сети основаны на механизме распространения информации, т.е. граф обрабатывается набором модулей, каждый из которых связан с узлом графа. В свою очередь модули связаны в соответствии со связями графа. Модули обновляют свое состояние и обмениваются информацией до тех пор, пока не достигнут устойчивого равновесия. Выходные данные GNN вычисляются в каждом узле на основе состояния модуля. Механизм распространения ограничен, чтобы гарантировать, что уникальное устойчивое состояние всегда существует.
В последние годы системы, основанные на вариантах графовых нейронных сетей, таких как graph convolutional network (GCN), graph attention network (GAT), gated graph neural network (GGNN), продемонстрировали высокую производительность при решении многих задач, обозначенных выше.
Описание
В графе каждый узел определяется его признаками и связанными узлами. Целью GNN является изучение состояния встраивания , которое содержит информацию об окрестностях для каждого узла. Состояние встраивания - это s-мерный вектор из вершины , который может быть использован для получения выхода (метки узла).
Пусть - это параметрическая функция, называемая локальной переходной функцией, которая является общей для всех узлов и обновляет состояние узла в соответствии с входной окрестностью. Также пусть - локальная выходная функция, которая описывает, как выход был производен. Тогда и определяются следующим образом:
где являются признаками , признаками его ребер, состояний, и признаками узлов в окрестностях соответственно.
Пусть и - это векторы, построенные путем укладки всех состояний, всех выходных данных, всех признаков и всех признаков узлов соответственно. Тогда мы можем представить уравнения в более компактной форме:
где - это глобальная функция перехода, а - глобальная выходная функция, которая является сложенной версией и для всех узлов в графе соответственно. Значение является фиксированным и однозначно определяется в предположением о том, что - это карта сжатия.
С учетом теоремы Банаха о неподвижной точке GNN использует следующую классическую итерационную схему для вычисления состояния: , где обозначает -ую итерацию . Динамическая система из этого уравнения сходится экспоненциально быстро к решению уравнения для любого начального значения . Стоит отметить, что вычисления описанные в и , могут быть интерпретированы как нейронные сети с прямой связью.
Следующие задачей становится поиск параметров и . С помощью целевой информации ( для конкретного узла) для контроля, функция потерь может быть вычислена следующим образом:
где - это число контролируемых узлов. Алгоритм обучения основан на стратегии градиентного спуска и состоит из следующих шагов:
- Состояния итеративно обновляются до времени . Они стремятся к фиксированному значению .
- Градиент весов вычисляется из функции потерь.
- Веса обновляются в соответствии с градиентом, вычисленным на последнем шаге.
Ограничения
Несмотря на то, что экспериментальные результаты показали, что GNN является мощной архитектурой для моделирования структурных данных, существует еще несколько ограничений для обычного GNN.
Во-первых, итеративно обновлять скрытые состояния узлов для фиксированной точки неэффективно. Если ослабить предположение о неподвижной точке, мы можем спроектировать многослойную GNN, чтобы получить стабильное представление узла и его окрестности.
Во-вторых, GNN использует одни и те же параметры в итерации, в то время как большинство популярных нейронных сетей используют разные параметры в разных слоях, которые служат в качестве метода извлечения иерархических признаков.
В-третьих, есть также некоторые информативные признаки на краях, которые не могут быть эффективно смоделированы обычной GNN. Например, ребра в графе знаний имеют тип отношений, и распространение сообщения через разные ребра должно быть различным в зависимости от их типов. Кроме того, поиск скрытых состояния ребер, также является важной проблемой.
Наконец, нецелесообразно использовать фиксированные точки, если мы сосредоточимся на представлении узлов вместо графиков, поскольку распределение представления в фиксированной точке будет гораздо более гладким по значению и менее информативным для различения каждого узла.