Симуляция одним распределением другого — различия между версиями
Geralt (обсуждение | вклад) м (→Симуляция распределений) |
Borisov (обсуждение | вклад) (→Распределение) |
||
| Строка 1: | Строка 1: | ||
==Распределение== | ==Распределение== | ||
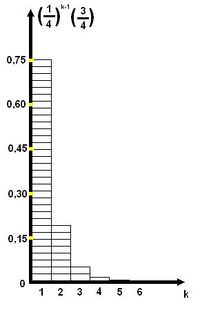
[[Файл:Распределение1_4.JPG|200px|thumb|right|Геометрическое распределение с p = 3/4]] | [[Файл:Распределение1_4.JPG|200px|thumb|right|Геометрическое распределение с p = 3/4]] | ||
| − | '''Распределение — '''одно из основных понятий теории вероятностей и математической | + | '''Распределение — '''одно из основных понятий теории вероятностей и математической статистике. Распределение вероятностей какой-либо случайной величины задается в простейшем случае указанием возможных значений этой величины и соответствующих им вероятностей, в более сложных — т. н. функцией распределения или плотностью вероятности. |
==Примеры распределений== | ==Примеры распределений== | ||
Версия 21:39, 11 декабря 2011
Содержание
Распределение
Распределение — одно из основных понятий теории вероятностей и математической статистике. Распределение вероятностей какой-либо случайной величины задается в простейшем случае указанием возможных значений этой величины и соответствующих им вероятностей, в более сложных — т. н. функцией распределения или плотностью вероятности.
Примеры распределений
- Биномиальное распределение
- Нормальное распределение
- Равномерное распределение
Симуляция распределений
Рассмотрим следующий случай. Допустим, у нас есть честная монета. А нам надо получить распределения с вероятностями . Проведем следующий эксперимент. Подкинем монету дважды. И если выпадет два раза орел - эксперимент не удался, повторим его. Предположим, что у нас есть последовательность экспериментов. Вероятность успеха . Вероятность неудачи Сколько экспериментов будет проведено до того, как будет достигнут успех? Пусть случайная величина равна количествуэкспериментов, необходимых для достижения успеха. Тогда принимает значения и для
поскольку перед наступлением успешного эксперимента было проведено неуспешных. Распределение вероятности, удовлетворяющее этому уравнению называется геометрическим распределением. Так как можно посчитать математическое ожидание геометрического распределения.
Дисперсия вычисляется аналогично.
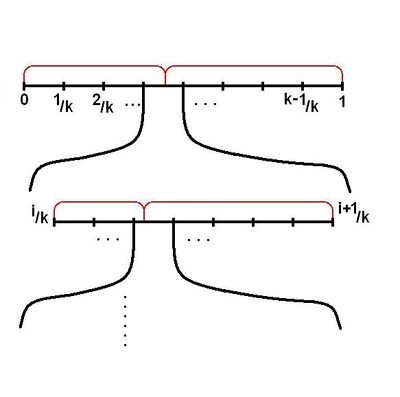
Обобщим. Допустим у нас есть распределение Нам нужно получить распределение :
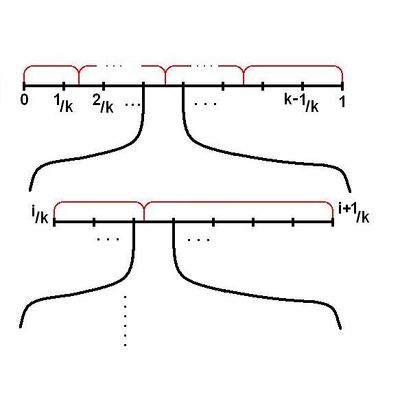
- Для начала рассмотрим случай, когда все а в распределениии количество элементарных исходов равно Проводим эксперимент, если попадаем в область пересекающуюся с и то увеличиваем ее и повторяем эксперимент. На рисунке ниже красным обозначенно распределение Вероятность того, что на этом шаге эксперимент не закончится — Математическое ожидание количества экспериментов — при
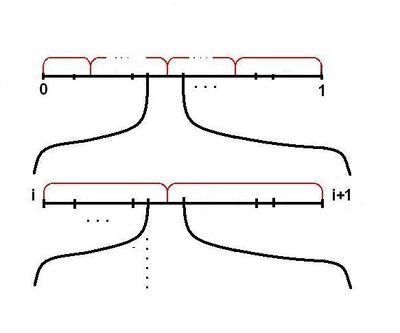
- Теперь рассмотри случай, когда все элементарные исходы по прежнему равновероятны а количество элементарных исходов распределения равно Повторим эксперимент раз. Отрезок разбился на отрезков. Стык будет не более, чем в половине отрезков. Математическое ожидание количества экспериментов
- Берем и пусть оно максимальной длины. Проводим экспериментов. все остальные еще меньше. Суммарная длина отрезков не больше Нужно
См. также
Литература
- Боровков А.А. Математическая статистика: оценка параметров, проверка гипотез. - М., Физматлит, 1984.
- Т. Кормен, Ч. Лейзерсон, Р. Ривест, К. Штайн - Алгоритмы. Построение и анализ 1244c.