Обсуждение участника:Qrort — различия между версиями

Материал из Викиконспекты
Перейти к: навигация, поиск
(→‎Кривые блеска)
(→‎Кривые блеска)
Строка 49: Строка 49:
 
# Для каждых двух точек кривой блеска <tex>(t_1, m_1), (t_2, m_2)</tex>, где <tex>t_i</tex> {{---}}} момент времени, <tex>m_i</tex> {{---}}} значение звездной величины, <tex>t_2 - t_1 = k * T</tex>, где <tex>k \in \mathbb{N}</tex>, <tex>T</tex> {{---}} некий временной интервал, пара значений <tex>(t_2 - t_1, m_2 - m_1)</tex> помещается в массив.
 
# Для каждых двух точек кривой блеска <tex>(t_1, m_1), (t_2, m_2)</tex>, где <tex>t_i</tex> {{---}}} момент времени, <tex>m_i</tex> {{---}}} значение звездной величины, <tex>t_2 - t_1 = k * T</tex>, где <tex>k \in \mathbb{N}</tex>, <tex>T</tex> {{---}} некий временной интервал, пара значений <tex>(t_2 - t_1, m_2 - m_1)</tex> помещается в массив.
 
# Полученные величины <tex>\Delta t, \Delta m</tex> округляются до ближайших из значений <tex>\delta m=\pm[0,0.1,0.2,0.3,0.5,1,1.5,2,2.5,3,5,8], \delta t=[\frac{1}{145},\frac{2}{145},\frac{3}{145},\frac{4}{145},\frac{1}{25},\frac{2}{25},\frac{3}{25},1.5,2.5,3.5,4.5,5.5,7,10,20,30,60,90,120,240,600,960,2000,4000]</tex>, тем самым перемещаясь в пространство <tex>23 * 24</tex>.
 
# Полученные величины <tex>\Delta t, \Delta m</tex> округляются до ближайших из значений <tex>\delta m=\pm[0,0.1,0.2,0.3,0.5,1,1.5,2,2.5,3,5,8], \delta t=[\frac{1}{145},\frac{2}{145},\frac{3}{145},\frac{4}{145},\frac{1}{25},\frac{2}{25},\frac{3}{25},1.5,2.5,3.5,4.5,5.5,7,10,20,30,60,90,120,240,600,960,2000,4000]</tex>, тем самым перемещаясь в пространство <tex>23 * 24</tex>.
−
# Строится изображение размера <tex>23 * 24</tex>, где интенсивность каждого пикселя пропорциональна количеству соответствующего элемента <tex>\Delta t, \Delta m</tex> в полученном выше массиве.<br><br>
+
# Строится изображение размера <tex>23 * 24</tex>, где интенсивность каждого пикселя пропорциональна количеству соответствующего элемента <tex>\Delta t, \Delta m</tex> в полученном выше массиве.
 +
После этого на полученных изображениях обучается сверточная нейронная сеть, которая может классифицировать тип кривой блеска с точностью 84.5%
 
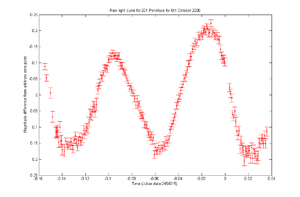
[[Файл:PenelopeLightCurve.png|300px|thumb|left|Кривая блеска астероида Пенелопа]]
 
[[Файл:PenelopeLightCurve.png|300px|thumb|left|Кривая блеска астероида Пенелопа]]
 
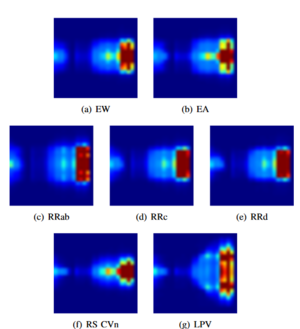
[[Файл:LightCurveImage.png|300px|thumb|right|Изображения для обучения сверточной нейронной сети]]
 
[[Файл:LightCurveImage.png|300px|thumb|right|Изображения для обучения сверточной нейронной сети]]

Версия 20:18, 12 января 2021


Машинное обучение в астрономии

Астрономия переживает стремительный рост объема и сложности данных. Существует множество проектов, исследующих и собирающих многоспектральные изображения неба, разновременную и многоволновую информацию, например, SDSS. Такие проекты предоставляют оцифрованные изображения неба, соответственно, в последние годы алгоритмы машинного обучения становятся все более популярными среди астрономов и в настоящее время используются для решения самых разнообразных задач; причиной этому служит большое количество доступных данных. В этой статье кратко приводится практическая информация о применении инструментов машинного обучения к астрономическим данным.

Классификация астрономических объектов по изображениям

Наличие в наборах данных большого количества объектов одного типа, но различных подтипов позволяет применить машинное обучение для решения задачи классификации на этих объектах.

Морфологическая классификация галактик

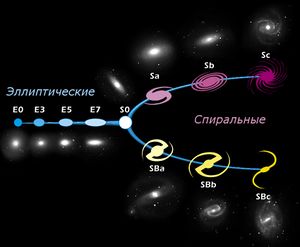
Классификация галактик, последовательность Хаббла

Одной из самых популярных тем классификации является морфологическая классификация галактик (англ. Morphology galaxy classification), позволяющая разделить их на различные типы по визуальным признакам. Для обучения моделей, призванных решать эту задачу, часто используют набор данных Galaxy Zoo, который является результатом волонтерского сотрудничества (ручной классификации галактик). Существует множество работ на эту тематику, использующих различные алгоритмы машинного обучения, как то: случайные леса[1], метод опорных векторов[2], нейронные сети[3]. Применение подходов машинного обучения в этом случае довольно прямолинейно, а разница между работами состоит в основном в представлении данных, выборе гиперпараметров и признаков классификации. Дополнительной сложностью вышеприведённых и прочих работ на ту же тему являются визуальные ограничения имеющихся изображений, такие, как мерцание, смещение, размытие и красное смещение. В настоящее время существуют методы, обеспечивающие вероятность неверной классификации объекта в 0.005[4].

Этой задачей следует заниматься, так как возможность находить тип галактик необходима для изучения их эволюции, а также является необходимым умением для множества задач наблюдательной космологии (англ. Observational cosmology), например, для нахождения кривых блеска.

Точность классификации различных алгоритмов на данных Galaxy Zoo[5]






Выявление аномалий

Интересной возможностью некоторых классификаторов является способ с помощью них найти объекты, которые трудно поддаются классификации, соответственно, могут принадлежать к новым, неизученным типам галактик. Рассмотрим в качестве примера случайные леса.

Случайные леса могут быть использованы для определения некоей меры схожести объектов без меток[6]. Чтобы перейти от задачи обучения без учителя к задаче обучения с учителем,которую можно решать с помощью случайного леса, применяется следующая идея:

  1. Пусть набор данных имеет вид таблицы [math]N \cdot M[/math], где каждая строка представляет объект с [math]M[/math] признаками. Построим другую матрицу размера [math]N \cdot M[/math], где значениями каждого столбца будет выборка из частного распределения соответствующего признака в исходном наборе данных. Такая матрица называется синтетическим набором данных (англ. synhtetic dataset). Альтернативным вариантом построения такой матрицы является случайная перестановка каждого столбца исходной матрицы.
  2. Пометим каждый объект исходного набора данных как принадлежащий классу [math]A[/math], а каждый объект синтетического набора данных как принадлежащий классу [math]B[/math]. Обучим случайный лес на этой выборке.

На этом этапе случайный лес способен определять наличие ковариации, ведь она присутствует только в исходном наборе данных. Как следствие, самыми важными признаками объектов будут являться признаки, имеющие корреляцию с другими. Расстояние между объектами определяется следующим образом: Каждая пара объектов передается во все решающие деревья случайного леса, и их схожесть описывается как количество деревьев, которые классифицировали оба объекта как принадлежащие классу [math]A[/math], причем оба объекта должны достигнуть одного и того же листа в дереве.

Таким методом можно пользоваться, например, для нахождения в больших объемах данных объектов, не похожих на большинство других, для отдельного их изучения. В частности, с помощью такого алгоритма можно найти необычные типы галактик[7].

Анализ астрономических явлений по спектральным данным

Классификация корональных выбросов массы

Признаки, использующиеся для классификации корональных выбросов массы

Машинное обучение может быть использовано для классификации[8] корональных выбросов массы, определения их силы, источника и направления. Метод состоит в выборке определенного набора параметров выброса по данным спектрометрического коронографа LASCO, а затем применения к этим данным метода опорных векторов.

Работа имеет большое практическое значение, так как корональные выбросы массы могут прерывать радиопередачу, наносить повреждения спутникам и линиям электропередачи, если они направлены в сторону Земли и имеют достаточную скорость и объем, чтобы достичь ее атмосферы[9].

Изучение астрономических параметров

Красное смещение

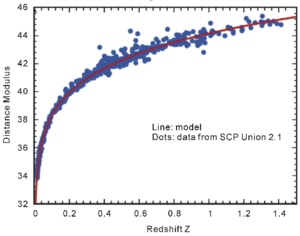
Зависимость расстояния от красного смещения

Красное смещение (англ. redshift) — астрономическое явление изменения длина волны наблюдаемого объекта. Важным свойством величины красного смещения является то, что через него, пользуясь законом Хаббла, можно высчитать примерное расстояние до объекта. Соответственно, красное смещение является важным астрономическим параметром, и при исследовании некоторых объектов будет полезным знать эту величину для вычисления других признаков объекта или заключения выводов о каких-либо закономерностях в наличествующих данных.

Красное смещение может быть вычислено при помощи спектральных данных объекта (англ. spectroscopic redshift), однако существуют другие методики, позволяющие в некоторых случаях определить примерную величину смещения по фотографии, пользуясь цветовыми характеристиками и яркостью объекта (англ. photometric redshift). Задачу нахождения величины фотометрического красного смещения можно переформулировать как задачу регрессии на соответствующих данных. Для решения такой задачи на популярных астрономических данных может быть использовано множество известных моделей машинного обучения, к примеру, случайные леса[10], нейронные сети[11] и идеи композиции нескольких моделей[12]. В настоящее время существуют алгоритмы, основанные на сверточных нейронных сетях, по предсказаниям которых можно восстановить расстояния до галактик, отличающихся от расстояний, вычисленных при помощи значений спектроскопического красного смещения, на несколько мегапарсек[13], что является высокой точностью в астрономических масштабах (примерно 10 процентов от среднего размера войда)

Кривые блеска

Кривая блеска (англ. light curve) — функция изменения звездной величины (в базовом понимании яркости) во времени. Кривая блеска позволяет определить целый ряд физических свойств тела, в частности, период обращения, продолжительность затмения, отношение радиуса звезды к радиусу орбиты тела. Соответственно, разделение кривых блеска на типы позволяет лучше изучить структуры астрономических систем.

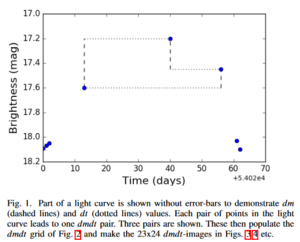
Классифицировать кривые блеска можно при помощи сверточных нейронных сетей[14]. Для этого необходимо представить функцию блеска в виде изображения. Это преобразование проводится следующим образом:

  1. Для каждых двух точек кривой блеска [math](t_1, m_1), (t_2, m_2)[/math], где [math]t_i[/math] —} момент времени, [math]m_i[/math] —} значение звездной величины, [math]t_2 - t_1 = k * T[/math], где [math]k \in \mathbb{N}[/math], [math]T[/math] — некий временной интервал, пара значений [math](t_2 - t_1, m_2 - m_1)[/math] помещается в массив.
  2. Полученные величины [math]\Delta t, \Delta m[/math] округляются до ближайших из значений [math]\delta m=\pm[0,0.1,0.2,0.3,0.5,1,1.5,2,2.5,3,5,8], \delta t=[\frac{1}{145},\frac{2}{145},\frac{3}{145},\frac{4}{145},\frac{1}{25},\frac{2}{25},\frac{3}{25},1.5,2.5,3.5,4.5,5.5,7,10,20,30,60,90,120,240,600,960,2000,4000][/math], тем самым перемещаясь в пространство [math]23 * 24[/math].
  3. Строится изображение размера [math]23 * 24[/math], где интенсивность каждого пикселя пропорциональна количеству соответствующего элемента [math]\Delta t, \Delta m[/math] в полученном выше массиве.

После этого на полученных изображениях обучается сверточная нейронная сеть, которая может классифицировать тип кривой блеска с точностью 84.5%

Кривая блеска астероида Пенелопа
Изображения для обучения сверточной нейронной сети
Преобразование кривой блеска в множество точек на плоскости

heading

или для классификации звезд и галактик (возможности отличать первые от вторых).[15]

Cлучайные леса

Список признаков объекта, использующийся в классификации звезд и галактик

Случайные леса (англ. random forest) используются для решения задач классификации и регрессии. В пример можно привести следующие исследования:

  • Определение величины красного смещения по изображению[16]
  • Классификация[17] кратковременных астрономических событий и переменных звезд
  • Классификация звезд и галактик[18]

Нейронные сети

Нейронные сети (англ. Artificial neural networks, ANN) используются для решения задач классификации и регрессии. В пример можно привести следующие исследования:

Обучение без учителя

Алгоритмы обучения без учителя применительно к астрономии имеют особое значение для научных исследований, поскольку они могут быть использованы для извлечения новых знаний из существующих наборов данных и могут способствовать новым открытиям.

K-means

Понятно, что классические алгоритмы кластеризации также могут быть применены к астрономическим данным. K-means применяется в астрономии в разных контекстах, например, для изучения спектральных классов звезд, галактик и астероидов, рентгеновского спектра объектов и так далее.[24][25][26]

Иерархическая кластеризация

Иерархическая кластеризация также применима к астрономическим данным, например, к рентгеновским спектрам, изображениям галактик и спектрам поглощения межзвездного газа.[27][28][29][30]

Примечания

Источники информации

  1. ↑ https://arxiv.org/abs/1611.07526
  2. ↑ Huertas-Company, M., Rouan, D., Tasca, L.,Soucail, G., & Le F`evre, O. 2008, A&A, 478,971
  3. ↑ Banerji, M., Lahav, O., Lintott, C. J., et al. 2010,MNRAS, 406, 342
  4. ↑ Miller, A. A., Kulkarni, M. K., Cao, Y., et al.2017, AJ, 153, 73
  5. ↑ arXiv:1901.07047 [astro-ph.IM]
  6. ↑ Shi, T., & Horvath, S. 2006, Journal ofComputational and Graphical Statistics, 15, 118
  7. ↑ Baron, D., & Poznanski, D. 2017, MNRAS, 465,4530
  8. ↑ Qu, M., Shih, F.Y., Jing, J. et al. Automatic Detection and Classification of Coronal Mass Ejections. Sol Phys 237, 419–431 (2006)
  9. ↑ https://en.wikipedia.org/wiki/Coronal_mass_ejection
  10. ↑ Carliles, S., Budav ́ari, T., Heinis, S., Priebe, C., &Szalay, A. S. 2010, ApJ, 712, 511
  11. ↑ Vanzella, E., Cristiani, S., Fontana, A., et al.2004, A&A, 423, 761
  12. ↑ https://doi.org/10.1051/0004-6361/201731326
  13. ↑ https://doi.org/10.1051/0004-6361/201937382
  14. ↑ Mahabal, A., Sheth, K., Gieseke, F., et al. 2017,ArXiv e-prints, arXiv:1709.06257
  15. ↑ Kov ́acs, A., & Szapudi, I. 2015, MNRAS, 448,1305
  16. ↑ Carliles, S., Budav ́ari, T., Heinis, S., Priebe, C., &Szalay, A. S. 2010, ApJ, 712, 511
  17. ↑ Bloom, J. S., Richards, J. W., Nugent, P. E., et al.2012, PASP, 124, 1175
  18. ↑ Miller, A. A., Kulkarni, M. K., Cao, Y., et al.2017, AJ, 153, 73
  19. ↑ Vanzella, E., Cristiani, S., Fontana, A., et al.2004, A&A, 423, 761
  20. ↑ Banerji, M., Lahav, O., Lintott, C. J., et al. 2010,MNRAS, 406, 342
  21. ↑ Ellison, S. L., Teimoorinia, H., Rosario, D. J., &Mendel, J. T. 2016, MNRAS, 458, L34
  22. ↑ Mahabal, A., Sheth, K., Gieseke, F., et al. 2017,ArXiv e-prints, arXiv:1709.06257
  23. ↑ Huertas-Company, M., Primack, J. R., Dekel, A.,et al. 2018, ApJ, 858, 114
  24. ↑ Hojnacki, S. M., Kastner, J. H., Micela, G.,Feigelson, E. D., & LaLonde, S. M. 2007, ApJ,659, 585
  25. ↑ Galluccio, L., Michel, O., Bendjoya, P., & Slezak,E. 2008, in American Institute of Physics
  26. ↑ Simpson, J. D., Cottrell, P. L., & Worley, C. C.2012, MNRAS, 427, 1153
  27. ↑ Hojnacki, S. M., Kastner, J. H., Micela, G.,Feigelson, E. D., & LaLonde, S. M. 2007, ApJ,659, 585
  28. ↑ Baron, D., Poznanski, D., Watson, D., et al. 2015,MNRAS, 451, 332
  29. ↑ Hocking, A., Geach, J. E., Davey, N., & Sun, Y.2015, ArXiv e-prints: 1507.01589,arXiv:1507.01589
  30. ↑ Peth, M. A., Lotz, J. M., Freeman, P. E., et al.2016, MNRAS, 458, 963
Источник — «http://neerc.ifmo.ru/wiki/index.php?title=Обсуждение_участника:Qrort&oldid=77973»