АВЛ-дерево — различия между версиями
Sementry (обсуждение | вклад) м |
Sementry (обсуждение | вклад) м |
||
| Строка 1: | Строка 1: | ||
| − | |||
'''АВЛ-дерево''' {{---}} двоичное дерево поиска, в котором поддерживается следующее свойство: для каждой его вершины высота её двух поддеревьев различается не более чем на 1. | '''АВЛ-дерево''' {{---}} двоичное дерево поиска, в котором поддерживается следующее свойство: для каждой его вершины высота её двух поддеревьев различается не более чем на 1. | ||
| − | + | ||
АВЛ-деревья названы по первым буквам фамилий их изобретателей, Г. М. Адельсона-Вельского и Е. М. Ландиса, которые впервые предложили использовать АВЛ-деревья в 1962 году. | АВЛ-деревья названы по первым буквам фамилий их изобретателей, Г. М. Адельсона-Вельского и Е. М. Ландиса, которые впервые предложили использовать АВЛ-деревья в 1962 году. | ||
| Строка 9: | Строка 8: | ||
Можно показать, что в AVL-дереве высоты <tex>h</tex> не менее, чем <tex>F_h = \Omega(\varphi^h)</tex> вершин, где <tex>F_h - h</tex>-ое число Фиббоначи, <tex>\varphi = \frac{ \sqrt{5}+1}{2}</tex>. Делая замену <tex>h = \log_\varphi{n}</tex>, получаем, что высота AVL-дерева из n вершин - <tex>O(\log{n})</tex>. | Можно показать, что в AVL-дереве высоты <tex>h</tex> не менее, чем <tex>F_h = \Omega(\varphi^h)</tex> вершин, где <tex>F_h - h</tex>-ое число Фиббоначи, <tex>\varphi = \frac{ \sqrt{5}+1}{2}</tex>. Делая замену <tex>h = \log_\varphi{n}</tex>, получаем, что высота AVL-дерева из n вершин - <tex>O(\log{n})</tex>. | ||
== Балансировка == | == Балансировка == | ||
| − | |||
'''Балансировкой вершины''' называется операция, которая в случае разницы высот левого и правого поддеревьев <tex>|h(L) - h(R)| = 2</tex>, изменяет связи предок-потомок в поддереве данной вершины так, чтобы восстановилось свойство дерева <tex>|h(L) - h(R)| \le 1</tex>, иначе ничего не меняет. | '''Балансировкой вершины''' называется операция, которая в случае разницы высот левого и правого поддеревьев <tex>|h(L) - h(R)| = 2</tex>, изменяет связи предок-потомок в поддереве данной вершины так, чтобы восстановилось свойство дерева <tex>|h(L) - h(R)| \le 1</tex>, иначе ничего не меняет. | ||
| − | + | ||
Указанный результат получается вращениями поддерева данной вершины. Для балансировки вершины используются один из 4 типов вращений: | Указанный результат получается вращениями поддерева данной вершины. Для балансировки вершины используются один из 4 типов вращений: | ||
Версия 06:12, 22 марта 2011
АВЛ-дерево — двоичное дерево поиска, в котором поддерживается следующее свойство: для каждой его вершины высота её двух поддеревьев различается не более чем на 1.
АВЛ-деревья названы по первым буквам фамилий их изобретателей, Г. М. Адельсона-Вельского и Е. М. Ландиса, которые впервые предложили использовать АВЛ-деревья в 1962 году.
Содержание
Высота дерева
Высоту поддерева с корнем будем обозначать как , высоту поддерева — как .
Можно показать, что в AVL-дереве высоты не менее, чем вершин, где -ое число Фиббоначи, . Делая замену , получаем, что высота AVL-дерева из n вершин - .
Балансировка
Балансировкой вершины называется операция, которая в случае разницы высот левого и правого поддеревьев , изменяет связи предок-потомок в поддереве данной вершины так, чтобы восстановилось свойство дерева , иначе ничего не меняет.
Указанный результат получается вращениями поддерева данной вершины. Для балансировки вершины используются один из 4 типов вращений:
| Тип вращения | Иллюстрация | Когда используется |
|---|---|---|
| Малое левое вращение | 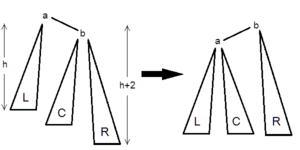
|
и . |
| Большое левое вращение | 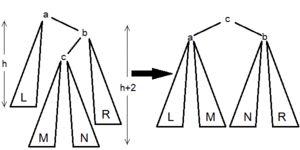
|
и . |
| Малое правое вращение | 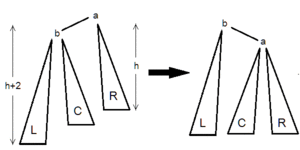
|
и . |
| Большое правое вращение | 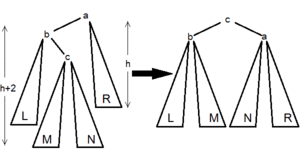
|
и . |
В каждом случае можно показать, что операция приводит к нужному результату и что полная высота уменьшается не более чем на 1 и не может увеличиться.
Все операции вращения, очевидно, требуют операций.
Добавление вершины
Процесс включения вершины состоит из двух частей:
- Прохода по пути поиска, пока не убедимся, что ключа в дереве нет.
- "Отступления" назад по пути поиска, вплоть до корня и пересчета высот в каждой вершине на обратном пути. При необходимости осуществляется балансировка.
Так как в процессе добавления вершины мы рассматриваем не более, чем вершин дерева, и для каждой запускаем балансировку не более одного раза, то суммарное количество операций при включении новой вершины в дерево составляет операций.
Удаление вершины
Для простоты опишем рекурсивный алгоритм удаления. Если вершина - лист, то удалим её и вызовем балансировку всех её предков в порядке от родителя к корню. Иначе найдём самую близкую по значению вершину и переместим её на место удаляемой вершины, при этом вызвав процедуру её удаления.
В результате указанных действий процедура удаления вызывается не более 3 раз, так как у вершины, удаляемой по 2-му вызову, нет хотя бы одного из поддеревьев. На балансировку суммарно тратится, как и ранее, операций. Таким образом, требуемое количество действий — .
Поиск вершины, минимум/максимум в дереве, etc.
Остальные операции не меняют структуры дерева, поэтому выполняются так же, как и в наивной реализации дерева поиска.