Параллельный алгоритм нахождения выпуклой оболочки — различия между версиями
Vladrus13 (обсуждение | вклад) |
Vladrus13 (обсуждение | вклад) (→Последовательный алгоритм) |
||
| Строка 7: | Строка 7: | ||
==Последовательный алгоритм== | ==Последовательный алгоритм== | ||
| − | [[Файл:Parallel-convexhull-not-parallel-1.png| | + | [[Файл:Parallel-convexhull-not-parallel-1.png|300px|thumb|right|Как мы будем двигаться]] |
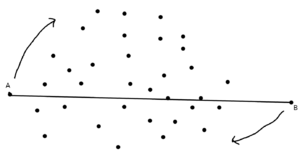
Давайте первым делом найдем самую левую A (при нескольких таких выбрать нижнюю) и самую правую B (при нескольких таких выбрать самую верхнюю) точку на плоскости. | Давайте первым делом найдем самую левую A (при нескольких таких выбрать нижнюю) и самую правую B (при нескольких таких выбрать самую верхнюю) точку на плоскости. | ||
| Строка 13: | Строка 13: | ||
Мы определенно знаем, что через них будет идти выпуклая оболочка, так как если она не будет идти через них, то это значит, что есть какой то отрезок между точками, который ниже и правее A, но это не так. Аналогично для правой верхней точки. Теперь будем строить от A до B верхнюю выпуклую оболочку для всех точек выше AB, и от B до A нижнюю выпуклую оболочку для всех точек ниже AB. | Мы определенно знаем, что через них будет идти выпуклая оболочка, так как если она не будет идти через них, то это значит, что есть какой то отрезок между точками, который ниже и правее A, но это не так. Аналогично для правой верхней точки. Теперь будем строить от A до B верхнюю выпуклую оболочку для всех точек выше AB, и от B до A нижнюю выпуклую оболочку для всех точек ниже AB. | ||
| − | Теперь рассмотрим верхнюю половину. Нижняя будет выполняться аналогично. Берем середину из самое левой точки и правой точки по координате x и делим наше множество точек на две части каким то образом. Теперь нам нужно сделать объединение за <tex>O(n)< | + | Теперь рассмотрим верхнюю половину. Нижняя будет выполняться аналогично. Берем середину из самое левой точки и правой точки по координате x и делим наше множество точек на две части каким то образом. Теперь нам нужно сделать объединение двух выпуклых оболочек за <tex>O(n)</tex>, для того, что бы итоговая асимптотика была <tex>O(nlog(n))</tex> |
| + | |||
| + | Прежде чем решать эту задачу, давайте решим такую задачу: | ||
| + | |||
| + | {{Задача | ||
| + | |definition = Нам дан выпуклый многоугольник, который был разрезан отрезком X, и взята верхняя часть. Так же дана точка, находящаяся выше X. Нужно провести касательную из точки к многоугольнику. | ||
| + | }} | ||
| + | |||
| + | [[Файл:Parallel-convex-hull-tangent.png|300px|thumb|right|Касательные]] | ||
| + | |||
| + | Мысленно представим соединение всех точек многоугольника с данной нам точкой. Заметим, что если мы воспользуемся [[Предикат_"левый_поворот"|предикатом "левый поворот"]], то сможем понять, находится ли точка, являющаяся касательной правее или левее, просто взяв предикат по точке куда ведем пересечение, данной точкой и следующей за точкой пересечения точкой. Проще говоря, нам нужно понять, "выше" ли находится прямая со следующей точкой или нет. Если оказалось, что она выше, то касательная находится выше. Если ниже, то касательная находится ниже. | ||
| + | |||
| + | Таким образом, мы можем за <tex>O(1)</tex> понимать для точки, дальше ли ее точка касательной или она была раньше. То есть у нас есть унимодальная функция, и нам нужно найти переход от 0 до 1. Похоже на задачу бинарного поиска. Давайте опишем шаги: | ||
| + | |||
| + | '''int''' l = 0, r = n - 2 | ||
| + | '''while''' 1 < r - l: | ||
| + | m = (l + r) / 2 | ||
| + | '''if''' left_turn(a[m], K, a[m + 1]) > 0: | ||
| + | l = m | ||
| + | else: | ||
| + | r = m | ||
| + | |||
| + | Нахождение касательной из точки на многоугольник работает за <tex>O(log(n))</tex> | ||
| + | |||
| + | {{Задача | ||
| + | |definition = Нам дано два выпуклых многоугольника A и B, которые были разрезаны отрезком X, и взята верхняя часть. Нужно провести такую касательную через 2 точки многоугольника, что все точки находятся либо на касательной либо ниже. | ||
| + | }} | ||
==Параллельный алгоритм== | ==Параллельный алгоритм== | ||
Версия 02:27, 26 ноября 2021
| Задача: |
| Пусть нам даны точки на плоскости. Нужно найти выпуклую оболочку на этих точках. |
| Определение: |
| Выпуклая оболочка — минимальная последовательность точек такая, что последовательное соединение этих точек дает выпуклый многоугольник, и в этом многоугольнике содержатся все точки. |
Последовательный алгоритм
Давайте первым делом найдем самую левую A (при нескольких таких выбрать нижнюю) и самую правую B (при нескольких таких выбрать самую верхнюю) точку на плоскости.
Мы определенно знаем, что через них будет идти выпуклая оболочка, так как если она не будет идти через них, то это значит, что есть какой то отрезок между точками, который ниже и правее A, но это не так. Аналогично для правой верхней точки. Теперь будем строить от A до B верхнюю выпуклую оболочку для всех точек выше AB, и от B до A нижнюю выпуклую оболочку для всех точек ниже AB.
Теперь рассмотрим верхнюю половину. Нижняя будет выполняться аналогично. Берем середину из самое левой точки и правой точки по координате x и делим наше множество точек на две части каким то образом. Теперь нам нужно сделать объединение двух выпуклых оболочек за , для того, что бы итоговая асимптотика была
Прежде чем решать эту задачу, давайте решим такую задачу:
| Задача: |
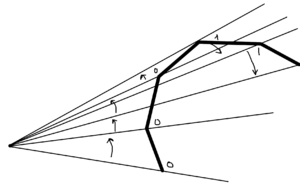
| Нам дан выпуклый многоугольник, который был разрезан отрезком X, и взята верхняя часть. Так же дана точка, находящаяся выше X. Нужно провести касательную из точки к многоугольнику. |
Мысленно представим соединение всех точек многоугольника с данной нам точкой. Заметим, что если мы воспользуемся предикатом "левый поворот", то сможем понять, находится ли точка, являющаяся касательной правее или левее, просто взяв предикат по точке куда ведем пересечение, данной точкой и следующей за точкой пересечения точкой. Проще говоря, нам нужно понять, "выше" ли находится прямая со следующей точкой или нет. Если оказалось, что она выше, то касательная находится выше. Если ниже, то касательная находится ниже.
Таким образом, мы можем за понимать для точки, дальше ли ее точка касательной или она была раньше. То есть у нас есть унимодальная функция, и нам нужно найти переход от 0 до 1. Похоже на задачу бинарного поиска. Давайте опишем шаги:
int l = 0, r = n - 2
while 1 < r - l:
m = (l + r) / 2
if left_turn(a[m], K, a[m + 1]) > 0:
l = m
else:
r = m
Нахождение касательной из точки на многоугольник работает за
| Задача: |
| Нам дано два выпуклых многоугольника A и B, которые были разрезаны отрезком X, и взята верхняя часть. Нужно провести такую касательную через 2 точки многоугольника, что все точки находятся либо на касательной либо ниже. |