Оценка качества в задачах классификации — различия между версиями
Melmon (обсуждение | вклад) (Обновление конспекта (Часть 1): Добавлена информация про Precison-recall кривую, кое-где исправлены опечатки и формулировки.) |
(→Общие понятия: Обновление конспекта (Часть 2): про бинарную классификацию и CM) |
||
| Строка 5: | Строка 5: | ||
* '''FN''' — false negative: классификатор неверно утверждает, что объект не принадлежит к рассматриваемому классу. | * '''FN''' — false negative: классификатор неверно утверждает, что объект не принадлежит к рассматриваемому классу. | ||
| − | '''Confusion matrix''' ('''матрица несоответствий''') | + | Здесь про TP, TN, FP, FN и понятия, через них выражающиеся, мы говорим в рамках одного класса бинарной классификации. То есть, в такой системе подразумевается, что реальное количество объектов класса 0 (для бинарного случая 0/1) может выражаться как <math>TP₀ + FN₀ = FP₁ + TN₁</math> |
| + | |||
| + | '''Confusion matrix''' ('''матрица ошибок / несоответствий / потерь, CM''') | ||
| + | — квадратная матрица размера k × k, где <tex>CM_{t,c}</tex> — число объектов класса <math>t</math>, | ||
| + | которые были квалифицированны как класс <math>c</math>, а <math>k</math> — число классов. Значения ячеек CM могут быть вычислены по формуле: | ||
| + | <tex>CM(y, \hat{y})_{t,c} = | ||
| + | \displaystyle\sum_{i = 1}^{n}[(y_i = t) ∧ (\hat{y_i} = c)]</tex>, где <tex>y_i</tex> - реальный класс объекта, а <tex>\hat{y_i}</tex> - предсказанный. | ||
| + | |||
| + | Для бинарного случая: | ||
{| class="wikitable" style="text-align: center;" | {| class="wikitable" style="text-align: center;" | ||
|- | |- | ||
Версия 11:55, 15 июня 2022
Общие понятия
- TP — true positive: классификатор верно отнёс объект к рассматриваемому классу.
- TN — true negative: классификатор верно утверждает, что объект не принадлежит к рассматриваемому классу.
- FP — false positive: классификатор неверно отнёс объект к рассматриваемому классу.
- FN — false negative: классификатор неверно утверждает, что объект не принадлежит к рассматриваемому классу.
Здесь про TP, TN, FP, FN и понятия, через них выражающиеся, мы говорим в рамках одного класса бинарной классификации. То есть, в такой системе подразумевается, что реальное количество объектов класса 0 (для бинарного случая 0/1) может выражаться как
Confusion matrix (матрица ошибок / несоответствий / потерь, CM) — квадратная матрица размера k × k, где — число объектов класса , которые были квалифицированны как класс , а — число классов. Значения ячеек CM могут быть вычислены по формуле: , где - реальный класс объекта, а - предсказанный.
Для бинарного случая:
| Принадлежит классу (P) | Не принадлежит классу (N) | |
|---|---|---|
| Предсказана принадлежность классу | TP | FP |
| Предсказано отсутствие принадлежности к классу | FN | TN |
Для многоклассовой классификации матрица несоответствий строится по тому же принципу:
| Предсказанный класс | Класс 1 (C₁) | Класс 2 (C₂) | Класс 3 (C₃) |
|---|---|---|---|
| 1 (P₁) | T₁ | F₁₂ | F₁₃ |
| 2 (P₂) | F₂₁ | T₂ | F₂₃ |
| 3 (P₃) | F₃₁ | F₃₂ | T₃ |
В этом случае TP, TN, FP и FN считаются относительно некоторого класса следующим образом:
Простые оценки
- Accuracy — (точность) показывает долю правильных классификаций. Несмотря на очевидность и простоту, является одной из самых малоинформативных оценок классификаторов.
- Recall — (полнота, sensitivity, TPR (true positive rate)) показывает отношение верно классифицированных объектов класса к общему числу элементов этого класса.
- Precision — (точность, перевод совпадает с accuracy)показывает долю верно классифицированных объектов среди всех объектов, которые к этому классу отнес классификатор.
- Specificity — показывает отношение верных срабатываний классификатора к общему числу объектов за пределами класса. Иначе говоря, то, насколько часто классификатор правильно не относит объекты к классу.
- Fall-out — (FPR (false positive rate)) показывает долю неверных срабатываний классификатора к общему числу объектов за пределами класса. Иначе говоря то, насколько часто классификатор ошибается при отнесении того или иного объекта к классу.
Ввиду того, что такие оценки никак не учитывают изначальное распределение классов в выборке (что может существенно влиять на полученное значение), также существуют взвешенные варианты этих оценок (в терминах многоклассовой классификации):
- Precision
- Recall
ROC кривая
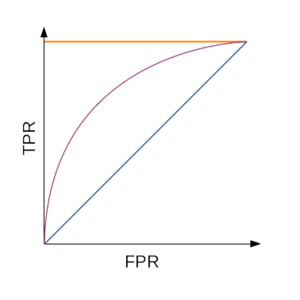
Для наглядной оценки качества алгоритма применяется ROC кривая. Кривая строится на плоскости, определённой TPR (по оси ординат) и FPR (по оси абсцисс).
Алгоритм построения кривой:
- Запустить классификатор на тестовой выборке
- Отсортировать результаты по уверенности классификатора в принадлежности объекта к классу
- Пока не кончились элементы:
- Взять объект с максимальной уверенностью
- Сравнить метку с реальной
- Пересчитать TPR и FPR на взятых объектах
- Поставить точку, если обе характеристики не NaN / ±∞
- Построить кривую по точкам
Таким образом: число точек не превосходит число объектов идеальному алгоритму соответствует ROC-кривая, проходящая через точку худшему алгоритму (например, монетке) соответствует прямая TPR = FPR.
Для численной оценки алгоритма по ROC-кривой используется значение площади под ней (AUC, area under curve). Идеальный алгоритм имеет AUC, равный 1, худший — 0,5.
Precision-Recall кривая
Обоснование: Чувствительность к соотношению классов.
Рассмотрим задачу выделения математических статей из множества научных статей. Допустим, что всего имеется 1.000.100 статей, из которых лишь 100 относятся к математике. Если нам удастся построить алгоритм , идеально решающий задачу, то его TPR будет равен единице, а FPR — нулю. Рассмотрим теперь "плохой" алгоритм, дающий положительный ответ на 95 математических и 50.000 нематематических статьях. Такой алгоритм совершенно бесполезен, но при этом имеет TPR = 0.95 и FPR = 0.05, что крайне близко к показателям идеального алгоритма. Таким образом, если положительный класс существенно меньше по размеру, то AUC-ROC может давать неадекватную оценку качества работы алгоритма, поскольку измеряет долю неверно принятых объектов относительно общего числа отрицательных. Так, алгоритм , помещающий 100 релевантных документов на позиции с 50.001-й по 50.101-ю, будет иметь AUC-ROC 0.95.
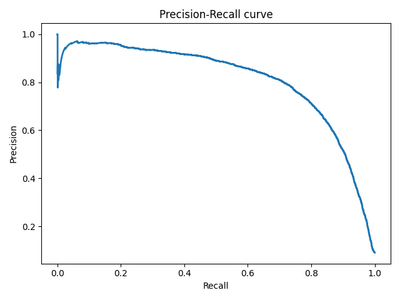
Precison-recall (PR) кривая. Избавиться от указанной проблемы с несбалансированными классами можно, перейдя от ROC-кривой к PR-кривой. Она определяется аналогично ROC-кривой, только по осям откладываются не FPR и TPR, а полнота (по оси абсцисс) и точность (по оси ординат). Критерием качества семейства алгоритмов выступает площадь под PR-кривой (англ. Area Under the Curve — AUC-PR)
F₁ score
Для общей оценки качества классификатора часто используют F₁ меру — среднее гармоническое между precision и recall:
F₁ мера так же может быть обобщена до Fβ:
Fβ измеряет эффективность классификатора учитывая recall в β раз более важным чем precision.
Для многоклассовой классификации с учётом изначального распределения по классам имеет смысл рассматривать микро- и макро- F меру: