Soft-Max и Soft-Arg-Max

Soft-Arg-Max

Постановка задачи

Пусть есть задача мягкой классификации:

Алгоритм выдает значения [math]L_{1}, L_{2},\ldots, L_{n}[/math], где [math]n[/math] — число классов.

[math]L_{i}[/math] — уверенность алгоритма в том, что объект принадлежит классу [math]i[/math], [math]L_{i} \in \left [ -\infty, +\infty\right ][/math]

Для этих значений необходимо найти такие [math]p_{1},\ldots,p_{n}[/math], что:

• [math]p_{i} \in \left [ 0, 1\right ][/math]
• [math]\sum_{i}p_{i}=1[/math]

То есть [math]p_{1},\ldots,p_{n}[/math] — распределение вероятностей

Для этого выполним преобразование:

[math]p_{i} = \frac{\exp\left(L_{i}\right)}{\sum_{i}\exp\left(L_{i}\right)}[/math]

Тогда выполняется следующее:

• [math]L_{i} \leqslant L_{j} \implies p_{i} \leqslant p_{j}[/math]
• Модель [math]a[/math], возвращающая [math]L_{i}[/math], после преобразования будет возвращать [math]p_{i}[/math] и останется дифференцируемой
• [math]p = \mathbf{softargmax}\left ( L \right )[/math]

Пусть [math]y = softargmax\left ( x \right )[/math], тогда:

[math]\frac{\partial y_{i}}{\partial x_{j}} = \begin{cases} &y_{i}\left ( 1 - y_{j} \right ),~i = j \\ &-y_{i}\cdot y_{j},~~~~~~i \neq j \end{cases} = y_{i}\left ( I\left [ i = j \right ] - y_{j}\right )[/math]

У soft-arg-max такое название, так как это, по сути, гладкая аппроксимация модифицированного arg-max.

Свойства soft-arg-max

• Вычисляет по вектору чисел вектор с распределением вероятностей
• Можно интерпретировать как вероятность нахождения максимума в [math]i[/math]-й координате
• [math]softargmax\left ( x - c,y-c,z-c\right )=softargmax\left ( x,y,z\right )[/math]
• Предыдущее свойство используют для устойчивости вычислений при [math]c=max\left ( x,y,z \right )[/math]

Модификация soft-arg-max

soft-arg-max[math]_{t}\left(x\right)=\frac{\exp\left(\frac{x_{i}}{t}\right)}{\sum\exp\left(\frac{x_{j}}{t}\right)}[/math]

Данная модификация полезна, когда необходимо контролировать распределение вероятностей, получаемое soft-arg-max. Чем больше параметр [math]t[/math], тем больше получаемые вероятности будут похожи на равномерное распределение.

Soft-Max

Плохой Soft-Max

рис.1 Плохой Soft-Max (помечен красным)

рис.2 Хороший Soft-Max (помечен оранжевым)

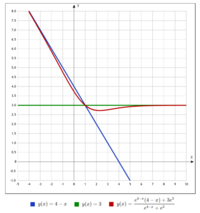
Зададим функцию soft-max таким образом:

soft-max[math]\left ( x_{1},\ldots,x_{n}\right ) = \frac{x_{i}~\cdot~\exp \left ( x_{i} \right )}{\sum_{j}\exp \left( x_{j} \right )} = \left \langle x, \right .[/math]soft-arg-max[math]\left . \left (x_{1},\ldots,x_{n} \right ) \right \rangle[/math]

Гладкая аппроксимация максимума. Математическое ожидание или средневзвешенное, где веса — экспоненты значений соответствующих элементов. Сохраняет некоторые свойства максимума:

• soft-max[math]\left ( a,a,a\right ) = a[/math]
• soft-max[math]\left ( x+a,y+a,z+a\right ) =[/math] soft-max[math]\left ( x,y,z\right ) + a[/math]

Заданный выше soft-max — "плохой" в связи с тем, что мы считаем средневзвешенное значение, которое всегда будет меньше максимума, что приведёт к проблемам с поиском максимума.

Хороший Soft-Max

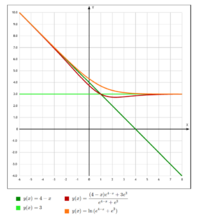
soft-max[math]\left ( x_{1},\ldots,x_{n}\right ) = \log\left(\sum_{i}\exp\left(x_{i}\right)\right)[/math]

• Не сохраняется свойство soft-max[math]\left(a,a,a\right)=a[/math]
• Производная равна soft-arg-max

В этом случае сохраняется монотонность, значит, не возникнет проблем с поиском минимума и максимума.

Связь между вариациями Soft-Max

Обозначим "плохой" soft-max как bad-soft-max. Тогда:

• bad-soft-max[math]\left(x_{1},\ldots,x_{n}\right)=\left \langle x, \right .[/math]soft-arg-max[math]\left . \left (x_{1},\ldots,x_{n} \right ) \right \rangle[/math]
• [math]\nabla[/math]soft-max[math]\left(x_{1},\ldots,x_{n}\right)=[/math] soft-arg-max[math]\left(x_{1},\ldots,x_{n}\right)[/math]
• [math]\log\left(\right.[/math]soft-arg-max[math]_{i}\left(x_{1},\ldots,x_{n}\right)\left.\right) = x_{i} -[/math]soft-max[math]\left(x_{1},\ldots,x_{n}\right)[/math]

Примечания

• В большинстве статей пишется soft-max, хотя вместо этого подразумевается soft-arg-max
• soft-arg-max можно называть также как обобщённая (многомерная) сигмоида
• soft-arg-max является алгоритмом подсчёта весов для soft-max

Источники

1. Лекция 7. Байесовские методы А. Забашта
2. Лекция 7. Автоматическое дифференцирование и нейронные сети С. Муравьёв