Двойное хэширование

Двойное хэширование

Двойное хэширование (double hashing) - один из лучших методов открытой адресации. Перебор ячеек хэш-таблицы, возникающий при двойном хешировании, обладает свойствами, присущими равномерному хешированию. При двойном хешировании хэш-функция [math] h [/math] имеет следующий вид:

[math] h(k,i) = (h_1(k) + i*h_2(k)) mod m [/math]

Вставка при двойном хэшировании

где [math] h_1 [/math] и [math] h_2 [/math] - вспомогательные хеш-функции, [math] m [/math] - размер хэш-таблицы. Иными словами, последовательность индексов исследуемых ячеек при работе с ключом [math] k [/math] представляет собой арифметическую прогрессию (по модулю [math] m [/math]) с первым членом [math] h_1(k) [/math] и шагом [math] h_2(k) [/math]. Следовательно, в данном случае последовательность исследования зависит от ключа k по двум параметрам - выбор начальной исследуемой ячейки и расстояние между двумя исследуемыми ячейками, так как оба параметра зависят от значения ключа.

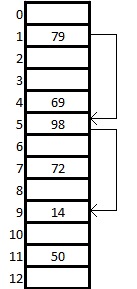
Пример вставки элемента при двойном хешировании приведен на рисунке справа.

Показана хэш-таблица размером 13 ячеек, в которой используются вспомогательные функции:

[math] h_1(k) = k mod 13 [/math]

[math] h_2(k) = 1 + k mod 11 [/math]

Мы хотим вставить ключ 14. Изначально [math] i = 0 [/math]. Тогда [math] h(14,0) = (h_1(14) + 0*h_2(14)) mod 13 = 1 [/math]. Но ячейка с индексом 1 занята, поэтому увеличиваем [math] i [/math] на 1 и пересчитываем значение хэш-функции. Делаем так, пока не дойдем до пустой ячейки. При [math] i = 2 [/math] получаем [math] h(14,2) = (h_1(14) + 2*h_2(14)) mod 13 = 9 [/math]. Ячейка с номером 9 свободна, значит записываем туда наш ключ.

Для того, чтобы последовательность исследования могла охватить всю таблицу, значение [math] h_2 [/math] должно быть взаимно простым с размером таблицы. Есть два удобных способа это сделать. Первый состоит в том, что в качестве размера таблицы используется простое число, а [math] h_2 [/math] возвращает натуральные числа, меньшие [math] m [/math]. Второй - размер таблицы является степенью двойки, а [math] h_2 [/math] возвращает нечетные значения.

Двойное хэширование превосходит другие в смысле количества последовательностей исследований. Это связано с тем, что каждая возможная пара [math] (h_1(k),h_2(k)) [/math] дает отличающуюся от других последовательность исследований.

Литература

• Томас Кормен, Чарльз Лейзерсон, Рональд Ривест, Клиффорд Штайн. Алгоритмы. Построение и анализ — Вильямс, 2010. - 1296с. — ISBN 978-5-8459-0857-4, 0-07-013151-1.