Формула включения-исключения — различия между версиями
GR1n (обсуждение | вклад) |
GR1n (обсуждение | вклад) |
||
| Строка 34: | Строка 34: | ||
| − | Очевидно, что <tex> | + | Очевидно, что <tex> B \cap A_n = \left( \bigcup \limits_{i=1}^{n-1}A_i \right) \cap A_n = \bigcup \limits_{i=1}^{n-1} \left( A_i \cap A_n \right) (**)</tex> |
| − | + | Опираясь на предположение индукции и равенство <tex> (**) </tex> имеем, что <tex> |B \cap A_n| = \sum \limits_{I \in 2^{N'}} (-1)^{|I|+1} \left| \bigcap \limits_{ j \in I} \left( A_j \cap A_n \right) \right| = \sum \limits_{I \in 2^{N'}} (-1)^{|I|+1} \left| \bigcap \limits_{ j\in I \cup \{ n \} } A_j \right| </tex> | |
Версия 03:16, 25 октября 2011
Формула включения–исключения — это комбинаторная формула, которая позволяет определить мощность объединения конечных множеств, если известны их мощности и мощности всех их возможных пересечений.
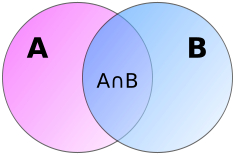
Например, в случае двух множеств формула включения—исключения имеет вид:
В сумме элементы пересечения учтены дважды, и, чтобы компенсировать это, мы вычитаем из правой части формулы. Справедливость этого рассуждения видна из диаграммы Эйлера–Венна для двух множеств, приведенной на рисунке справа.
Таким же образом и в случае множеств процесс нахождения количества элементов объединения состоит во включении всего, затем исключении лишнего, затем включении ошибочно исключенного и так далее, то есть в попеременном включении и исключении. Отсюда и происходит название формулы.
| Теорема: |
Пусть , тогда по формуле включения–исключения: |
| Доказательство: |
|
Доказываем теорему по индукции. Пусть — это количество множеств, мощность пересечения которых мы ищем. Для случая равенство обращается в тривиальное (). Для случая справедливость теоремы пояснена выше. Таким образом, — база индукции. Предположим, что для равенство верно. Докажем, что равенство истинно для
Равенство справедливо, потому что все наборы можно разбить на две группы :
Как видно из равенства, первое и третье слагаемое "отвечают" за вторую группу, а второе слагаемое за первую группу. Значит, равенство истинно и . Таким образом, для мы доказали, что равенство верно. Значит, индукционный переход верен, то есть теорема доказана. |