Отношение рёберной двусвязности — различия между версиями

Материал из Викиконспекты
Перейти к: навигация, поиск
(→‎Реберная двусвязность)
(→‎Реберная двусвязность)
Строка 25: Строка 25:
 
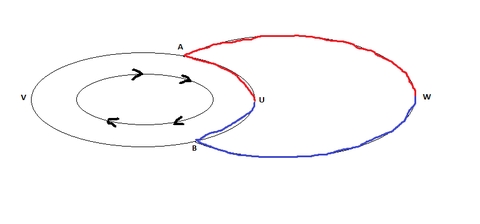
[[Файл:Gumno.png|right|480px|thumb|]] Пусть из <tex> u </tex> в <tex> v </tex> есть два реберно не пересекающихся пути. Их объединение будет реберно-простым циклом. Обозначим его за <tex> C </tex>.  
 
[[Файл:Gumno.png|right|480px|thumb|]] Пусть из <tex> u </tex> в <tex> v </tex> есть два реберно не пересекающихся пути. Их объединение будет реберно-простым циклом. Обозначим его за <tex> C </tex>.  
 
Вершина <tex> w </tex> реберно двусвязна с <tex> v </tex>. Назовем эти пути <tex> P_1 </tex> и <tex> P_2 </tex>.
 
Вершина <tex> w </tex> реберно двусвязна с <tex> v </tex>. Назовем эти пути <tex> P_1 </tex> и <tex> P_2 </tex>.
−
Пусть вершина <tex> a </tex> - первое пересечение <tex> P_1 </tex> с циклом.
+
Пусть вершина <tex> a </tex> - пересечение <tex> P_1 </tex> с циклом.
−
Пусть вершина <tex> b </tex> - первое пересечение <tex> P_2 </tex> с циклом.
+
Пусть вершина <tex> b </tex> - пересечение <tex> P_2 </tex> с циклом.
−
Рассматриваем два пути.
 
−
Первый - <tex> wa </tex> + часть цикла <tex> C </tex> <tex> au </tex> по часовой стрелке.
 
−
Второй - <tex> wb </tex> + часть цикла <tex> C </tex> <tex> bu </tex> против часовой стрелке.
 
  
−
Эти два пути реберно не пересекающиеся, а значит  <tex> u </tex> и  <tex> w </tex> реберно двусвязны.
+
Рассматриваем два пути <tex> wau и wbu </tex> таких, что части <tex> au и bu </tex> идут в разные стороны относительно часовой стрелки.
 +
 
 +
Наличие двух таких реберно не пересекающихся пути очевидно, а значит  <tex> u </tex> и  <tex> w </tex> реберно двусвязны.
  
 
}}
 
}}

Версия 22:26, 26 октября 2011

Эта статья требует доработки!
  1. Доказательство транзитивности отношения реберной двусвязности некорректно (убедитесь в этом) исправил.

Если Вы исправили некоторые из указанных выше замечаний, просьба дописать в начало соответствующего пункта (Исправлено).

Реберная двусвязность

Определение:
Две вершины [math]u[/math] и [math] v[/math] графа [math]G[/math] называются реберно двусвязными, если между этими вершинами существуют два реберно непересекающихся пути.


Теорема:
Отношение реберной двусвязности является отношением эквивалентности на вершинах.
Доказательство:
[math]\triangleright[/math]

Пусть [math]R[/math] - отношение реберной двусвязности.

Рефлексивность: [math](u, u)\in R. [/math] (Очевидно)

Симметричность: [math](u, v)\in R \Rightarrow (v, u)\in R. [/math] (Очевидно)

Транзитивность: [math](u, v)\in R [/math] и [math](v, w)\in R \Rightarrow (u, w)\in R. [/math]

Доказательство:

Gumno.png
Пусть из [math] u [/math] в [math] v [/math] есть два реберно не пересекающихся пути. Их объединение будет реберно-простым циклом. Обозначим его за [math] C [/math].

Вершина [math] w [/math] реберно двусвязна с [math] v [/math]. Назовем эти пути [math] P_1 [/math] и [math] P_2 [/math]. Пусть вершина [math] a [/math] - пересечение [math] P_1 [/math] с циклом. Пусть вершина [math] b [/math] - пересечение [math] P_2 [/math] с циклом.

Рассматриваем два пути [math] wau и wbu [/math] таких, что части [math] au и bu [/math] идут в разные стороны относительно часовой стрелки.

Наличие двух таких реберно не пересекающихся пути очевидно, а значит [math] u [/math] и [math] w [/math] реберно двусвязны.
[math]\triangleleft[/math]

Компоненты реберной двусвязности

Определение:
Компонентами реберной двусвязности графа, называют его подграфы, множества вершин которых - классы эквивалентности реберной двусвязности, а множества ребер - множества ребер из соответствующих классов эквивалентности.


См. также

Отношение вершинной двусвязности

Источники

- визуализатор ::компоненты связности

Литература

  • Харари Фрэнк Теория графов = Graph theory/Пер. с англ. и предисл. В. П. Козырева. Под ред. Г.П.Гаврилова. Изд. 2-е. — М.: Едиториал УРСС, 2003. — 60 с. — ISBN 5-354-00301-6
Источник — «http://neerc.ifmo.ru/wiki/index.php?title=Отношение_рёберной_двусвязности&oldid=12092»