Алгоритм Прима

Алгоритм Прима — алгоритм поиска минимального остовного дерева (minimum spanning tree, MST) во взвешенном неориентированном связном графе.

Идея

Данный алгоритм очень похож на алгоритм Дейкстры. Будем последовательно строить поддерево [math]F[/math] ответа в графе [math]G[/math], поддерживая приоритетную очередь [math]Q[/math] из вершин [math]G \setminus F[/math], имеющую ключом для вершины [math]v[/math] [math]\min\limits_{u \in F, (u,v) \in E}\{w(u,v)\}[/math] (вес минимального ребра из вершин [math]F[/math] в вершину [math]v[/math]). Также для каждой вершины очереди будем хранить [math]p(v)[/math] — вершину [math]u[/math], на которой достигается минимум в определении ключа. Множество ребер дерева [math]F[/math] поддерживается неявно, и равно [math]\left\{\left(v,p(v)\right)|v \in G \setminus \{r\} \setminus Q\right\}[/math], где [math]r[/math] — корень [math]F[/math]. Изначально [math]F[/math] пусто, в очереди все вершины с ключами [math]+\infty[/math]. Выберём произвольную вершину [math]r[/math] и присвоим её ключу [math]0[/math]. На каждом шаге будем извлекать минимальную вершину [math]v[/math] из приоритетной очереди и релаксировать все ребра [math]vu[/math], такие что [math]u \in Q[/math], выполняя при этом [math]\text{DECREASE-KEY}[/math] и обновление [math]p(v)[/math]. Ребро [math]\left(v,p(v)\right)[/math] при этом добавляется к ответу.

Реализация

[math]\text{Prim}(V, G, w)[/math]
  [math]for[/math] [math]v \in V[G][/math]
     [math] key[v] \leftarrow \infty [/math]
        [math]p[v] \leftarrow \text{NIL}[/math]
  [math]r \leftarrow [/math] [math]произвольная вершина в [/math][math]V[G][/math]
  [math]key[r] \leftarrow 0 [/math]
  [math]Q \leftarrow V[G] [/math]
  [math]while[/math] [math] Q \neq \emptyset [/math]
     [math]u \leftarrow \text{extract-min}(Q) [/math]
        [math]for[/math] [math] v \in Adj[u] [/math]
            [math]if[/math] [math]v \in Q[/math] [math]and[/math] [math]key[v] \gt  \omega(u, v) [/math]
              [math]then[/math] [math] p[v] \leftarrow u [/math]
                   [math]key[v] \leftarrow \omega(u, v)[/math]
                   [math]\text{decrease-key}(Q, v) [/math]

Ребра дерева восстанавливаются из его неявного вида после выполнения алгоритма.

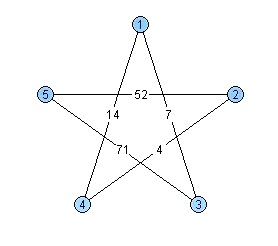
Пример работы алгоритма

Граф "звезда" с расставленными весами ребер

Таблица соответствует работе алгоритма на графе с картинки.

№ шага	key[]					p[]
	1	2	3	4	5
1)	[math]\infty [/math]	[math]\infty [/math]	[math]\infty [/math]	[math]\infty [/math]	[math]\infty [/math]	[math]-[/math]
2)	0	[math]\infty [/math]	[math]\infty [/math]	[math]\infty [/math]	[math]\infty [/math]	1
3)	0	[math]\infty [/math]	7	14	[math]\infty [/math]	1 3
4)	0	[math]\infty [/math]	7	14	71	4 1 3
5)	0	2	7	14	71	2 4 1 3
6)	0	2	7	14	71	5 2 4 1 3

Корректность

По поддерживаемым инвариантам после извлечения вершины [math]v[/math] ([math]v \neq r[/math]) из [math]Q[/math] ребро [math]\left(v,p(v)\right)[/math] является ребром минимального веса, пересекающим разрез [math]\left(F,Q\right)[/math]. Значит, по лемме о безопасном ребре, оно безопасно. Алгоритм построения MST, добавляющий безопасные ребра, причём делающий это ровно [math]|V|-1[/math] раз, корректен.

Оценка производительности

Производительность алгоритма Прима зависит от выбранной реализации приоритетной очереди, как и в алгоритме Дейкстры. Извлечение минимума выполняется [math]V[/math] раз, релаксация — [math]O(E)[/math] раз.

Структура данных для приоритетной очереди	Асимптотика времени работы
Наивная реализация	[math]O(V^2+E)[/math]
Двоичная куча	[math]O(E\log{V})[/math]
Куча Фибоначчи	[math]O(V\log{V}+E)[/math]

См. также

• Алгоритм Краскала

Литература

• Кормен, Томас Х., Лейзерсон, Чарльз И., Ривест, Рональд Л., Штайн Клиффорд Алгоритмы: построение и анализ, 2-е издание. Пер. с англ. — М.:Издательский дом "Вильямс", 2010. — с.653 — 656.— ISBN 978-5-8459-0857-5 (рус.)