Эргодическая марковская цепь — различия между версиями
Alina (обсуждение | вклад) |
Whiplash (обсуждение | вклад) |
||
| Строка 1: | Строка 1: | ||
| − | |||
{{Определение | {{Определение | ||
|definition=Марковская цепь называется эргодической, если существует дискретное распределение (называемое эргодическим) <tex>\pi = (\pi_1,\pi_2,\ldots )^{\top}</tex>, такое что <tex>\pi_i > 0,\; i \in \mathbb{N}</tex> и | |definition=Марковская цепь называется эргодической, если существует дискретное распределение (называемое эргодическим) <tex>\pi = (\pi_1,\pi_2,\ldots )^{\top}</tex>, такое что <tex>\pi_i > 0,\; i \in \mathbb{N}</tex> и | ||
:<tex>\lim\limits_{n \to \infty} p_{ij}^{(n)} = \pi_j, \quad \forall i=1,2, \ldots</tex>. | :<tex>\lim\limits_{n \to \infty} p_{ij}^{(n)} = \pi_j, \quad \forall i=1,2, \ldots</tex>. | ||
}} | }} | ||
| + | |||
=== Пример: === | === Пример: === | ||
[[File:Temp.gif|thumb|250px|Пример эргодической цепи]] | [[File:Temp.gif|thumb|250px|Пример эргодической цепи]] | ||
Версия 08:07, 15 декабря 2011
| Определение: |
Марковская цепь называется эргодической, если существует дискретное распределение (называемое эргодическим) , такое что и
|
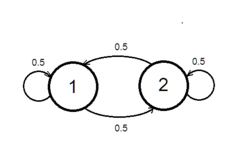
Пример:
Рассмотрим эксперимент по бросанию честной монеты. Тогда соответствующая этому эксперименту марковская цепь будет иметь 2 состояния. Рассмотрим матрицу, следующего вида: .
Такая матрица является стохастической, а, значит, корректно определяет марковскую цепь. Такая цепь является эргодической, так как существует эргодическое распределение , такое что .
См. также
Википедия: эргодическое распределение
Википедия: дискретное распределение
Литература
Дж. Кемени, Дж. Снелл "Конечные цепи Маркова"