Формула включения-исключения — различия между версиями
м |
|||
| Строка 1: | Строка 1: | ||
| − | '''Формула включения | + | '''Формула включения-исключения''' {{---}} комбинаторная формула, выражающая мощность объединения конечных множеств через мощности и мощности всех их возможных пересечений. |
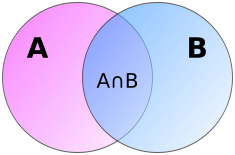
[[Файл:пересечение двух множеств.svg.png|thumb|right|Случай для двух множеств]] | [[Файл:пересечение двух множеств.svg.png|thumb|right|Случай для двух множеств]] | ||
| − | Для случая из двух множеств <tex> | + | Для случая из двух множеств <tex>A, B</tex> формула включения-исключения имеет следующий вид: |
<center> | <center> | ||
<tex> | A \cup B | = | A | + | B | - | A \cap B |</tex> | <tex> | A \cup B | = | A | + | B | - | A \cap B |</tex> | ||
</center> | </center> | ||
| − | В силу того, что в сумме <tex> | + | В силу того, что в сумме <tex>| A | + | B |</tex> элементы пересечения <tex>A \cap B</tex> учтены дважды, то уменьшаем текущее значение суммы на мощность пересечения, чтобы каждый элемент был подсчитан ровно один раз. Для наглядности воспользуемся диаграммой Эйлера{{---}}Венна для двух множеств, приведенной на рисунке справа. |
| − | Для случая с большим количеством рассматриваемых множеств <tex> n </tex> процесс нахождения количества элементов объединения состоит в поочередном включений ошибочно исключенного | + | Для случая с большим количеством рассматриваемых множеств <tex> n </tex> процесс нахождения количества элементов объединения состоит в поочередном включений ошибочно исключенного и исключений ошибочно включенного. Отсюда и происходит название формулы. |
Сформулируем и докажем теорему для нахождения мощности объединения произвольного количества множеств. | Сформулируем и докажем теорему для нахождения мощности объединения произвольного количества множеств. | ||
Версия 04:11, 22 декабря 2011
Формула включения-исключения — комбинаторная формула, выражающая мощность объединения конечных множеств через мощности и мощности всех их возможных пересечений.
Для случая из двух множеств формула включения-исключения имеет следующий вид:
В силу того, что в сумме элементы пересечения учтены дважды, то уменьшаем текущее значение суммы на мощность пересечения, чтобы каждый элемент был подсчитан ровно один раз. Для наглядности воспользуемся диаграммой Эйлера—Венна для двух множеств, приведенной на рисунке справа.
Для случая с большим количеством рассматриваемых множеств процесс нахождения количества элементов объединения состоит в поочередном включений ошибочно исключенного и исключений ошибочно включенного. Отсюда и происходит название формулы.
Сформулируем и докажем теорему для нахождения мощности объединения произвольного количества множеств.
| Теорема: |
Пусть , тогда по формуле включения—исключения: |
| Доказательство: |
|
Приведем два разноплановых доказательства теоремы. I. Комбинаторное доказательство теоремы. Рассмотрим некоторый элемент . Пусть . Тогда найдем число вхождений элемента в правую часть формулы.
Докажем, что В силу того, что , имеем , то равенство доказано. Таким образом, , то есть каждый элемент подсчитан в правой части формулы ровно один раз, то теорема доказана. II. Доказательство теоремы по индукции. Пусть — это количество множеств, мощность пересечения которых мы ищем. Для случая равенство обращается в тривиальное ( — истинно). Для случая справедливость теоремы пояснена выше. Таким образом, — база индукции. Предположим, что для равенство верно. Докажем, что равенство истинно для
Равенство справедливо, потому что все наборы можно разбить на две группы :
Как видно из равенства, первое и третье слагаемое "отвечают" за вторую группу, а второе слагаемое за первую группу. Значит, равенство истинно и . Таким образом, для мы доказали, что равенство верно. Значит, индукционный переход верен, то есть теорема доказана. |