Эргодическая марковская цепь

Определение:

Марковская цепь называется эргодической, если существует дискретное распределение (называемое эргодическим) [math]\pi = (\pi_1,\pi_2,\ldots )^{\top}[/math], такое что [math]\pi_i \gt 0,\; i \in \mathbb{N}[/math] и [math]\lim\limits_{n \to \infty} p_{ij}^{(n)} = \pi_j, \quad \forall i=1,2, \ldots[/math].

Марковскую цепь обладающую следующими свойствами называют слабо эргодическиой, если она обладает следующими свойствами:

1. Для любых двух различных вершин графа переходов [math]i,j \, (i\neq j)[/math] найдется такая вершина [math]k[/math] графа («общий сток»), что существуют ориентированные пути от вершины [math]i[/math] к вершине [math]k[/math] и от вершины [math]j[/math] к вершине [math]k[/math]. Замечание: возможен случай [math]k=i[/math] или [math]k=j[/math]; в этом случае тривиальный (пустой) путь от [math]i[/math] к [math]i[/math] или от [math]j[/math] к [math]j[/math] также считается ориентированным путем.
2. Нулевое собственное число матрицы интенсивности невырождено.
3. При [math]t \to \infty[/math] матрица переходных вероятностей стремится к матрице, у которой все строки совпадают (и совпадают, очевидно, с равновесным распределением).

Примеры графов переходов для цепей Маркова: a) цепь не является слабо эргодической (не существует общего стока [math]^{[1]}[/math] для состояний [math]A_2, \, A_3[/math]); b) слабо эргодическая, но не эргодическая цепь (граф переходов является слабо-связным [math]^{[2]}[/math]) c) эргодическая цепь (сильно-связный [math]^{[3]}[/math] граф переходов).

Основная теорема об эргодических распределениях

Теорема (Основная теорема об эргодических распределениях):

Пусть [math]\{X_n\}_{n \ge 0}[/math] - цепь Маркова с дискретным пространством состояний и матрицей переходных вероятностей [math]P = (p_{ij}),\; i,j=1,2,\ldots[/math]. Тогда эта цепь является эргодической тогда и только тогда, когда она Неразложима [math]^{[4]}[/math]; Положительно возвратна [math]^{[5]}[/math]; Апериодична [math]^{[6]}[/math]. Эргодическое распределение [math]\mathbf{\pi}[/math] тогда является единственным решением системы: [math]\sum\limits_{i=0}^{\infty} \pi_i = 1,\; \pi_j \ge 0,\; \pi_j = \sum\limits_{i=0}^{\infty} \pi_i\, p_{ij},\quad \, j\in \mathbb{N}[/math].

Пример

Пример эргодической цепи

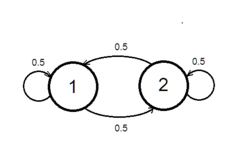
Рассмотрим эксперимент по бросанию честной монеты. Тогда соответствующая этому эксперименту марковская цепь будет иметь 2 состояния. Рассмотрим матрицу, следующего вида: [math]p_{ij}=0.5, i,j=1,2[/math].

Такая матрица является стохастической, а, значит, корректно определяет марковскую цепь. Такая цепь является эргодической, так как существует эргодическое распределение [math]\pi = (0.5,0.5)^{\top}[/math], такое что [math]\lim\limits_{n \to \infty} p_{ij}^{(n)} = \pi_j, i=1,2[/math].

См. также

• Марковская цепь

• Регулярная марковская цепь

Примечания

1. Общий сток - такая [math]k[/math] вершина графа, что для любых двух различных вершин графа переходов [math]i,j \, (i\neq j)[/math], существуют ориентированные пути от вершины [math]i[/math] к вершине [math]k[/math] и от вершины [math]j[/math] к вершине [math]k[/math].
2. Ориентированный граф называется слабо-связным, если является связным неориентированный граф, полученный из него заменой ориентированных рёбер неориентированными.
3. Ориентированный граф называется сильно-связным, если в нём существует (ориентированный) путь из любой вершины в любую другую, или, что эквивалентно, граф содержит ровно одну сильно связную компоненту.
4. Если цепь Маркова такова, что её состояния образуют лишь один неразложимый класс [math]^{[7]}[/math], то она называется неразложимой.
5. Возвратное состояние [math]i[/math] называется положительным, если [math] \mathbb{E}[T_i] = \sum\limits_{n=1}^{\infty} n f^{(n)}_{ii} \lt \infty[/math] [math]([/math]где [math]f_{ii}^{(n)} = \mathbb{P}(X_n = i,\; X_k \not= i, \, k=1,\ldots, n-1 \mid X_0 = i )[/math] — вероятность, выйдя из состояния [math]i[/math], вернуться в него ровно за [math]n[/math] шагов[math])[/math].
6. Если [math]d(j) = 1[/math], то состояние j называется апериодическим [math](d(j) = \gcd \left(n \in \mathbb{N} \mid p_{jj}^{(n)} \gt 0 \right)[/math], где [math]gcd[/math] обозначает наибольший общий делитель, называется периодом состояния [math]j[/math], [math]p_{jj}^{(n)}[/math] матрица переходных вероятностей за [math]n[/math] шагов[math])[/math].
7. Свойство сообщаемости порождает на пространстве состояний отношение эквивалентности. Порождаемые классы эквивалентности называются неразложимыми классами.

Ссылки

• Эргодическое распределение - Википедия

• Дискретное распределение - Википедия

Литература

Дж. Кемени, Дж. Снелл "Конечные цепи Маркова"