Алгоритм A* — различия между версиями
м (→Ссылки) |
|||
| Строка 3: | Строка 3: | ||
В процессе работы алгоритма для вершин рассчитывается функция <tex>f(v) = g(v) + h(v)</tex>, где | В процессе работы алгоритма для вершин рассчитывается функция <tex>f(v) = g(v) + h(v)</tex>, где | ||
*<tex>g(v)</tex> {{---}} наименьшая стоимость пути в <tex>v</tex> из стартовой вершины, | *<tex>g(v)</tex> {{---}} наименьшая стоимость пути в <tex>v</tex> из стартовой вершины, | ||
| − | *<tex>h(v)</tex> {{---}} эвристическое приближение стоимости пути от <tex>v</tex> до конечной цели. <tex>h(v)</tex> должна быть эвристически допустимой, то есть не должна переоценивать рассояние до цели | + | *<tex>h(v)</tex> {{---}} эвристическое приближение стоимости пути от <tex>v</tex> до конечной цели. <tex>h(v)</tex> должна быть эвристически допустимой, то есть не должна переоценивать рассояние до цели. |
| − | Чем меньше | + | Чем меньше , тем раньше вершина будет открыта и исследована алгоритмом. Таким образом открытые алгоритмом вершины хранятся в очереди с приоритетом по значению <tex>f(v)</tex>. А* действует подобно [[Алгоритм Дейкстры | алгоритму Дейкстры]] и просматривает среди всех маршрутов ведущих к цели сначала те, которые благодаря имеющейся информации(эвристическая функция) в данный момент являются наилучшими, причем алгоритм учитывает путь уже пройденный до текущей вершины. |
| + | |||
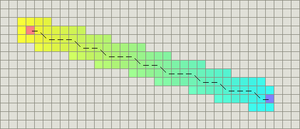
| + | Поведение алгоритма сильно зависит от того, какая эвристика используется. В свою очередь, выбор эвристики зависит[[Файл:Diagonal.png|thumb|right|Пример А* на сетке с возможностью ходить в восьми напрвлениях]] от постановки задачи. Часто А* используется для моделирования перемещения по поверхности, покрытой [http://deep-beta.co.uk/wp-content/uploads/2010/11/terrain.0.3+grid.png координатной сеткой]. | ||
| + | |||
| + | Если мы можем перемещаться в четырех направлениях, в качестве эвристики стоит выбрать [http://en.wikipedia.org/wiki/Manhattan_distance манхэттенское расстояние] | ||
| + | <tex>h(v) = |{v.x-goal.x}| + |{v.y-goal.y}|</tex>. | ||
| + | |||
| + | [http://ru.wikipedia.org/wiki/Расстояние_Чебышева Расстояние Чебышева] <tex>h(v) = \max{(|{v.x-goal.x}|, |{v.y-goal.y}|)}</tex> применяется когда к четырем направлениям добавляются диагонали. | ||
| + | |||
| + | Если передвижение не ограниченно сеткой, то можно использовать евклидово расстояние по прямой <tex>h(v) = \sqrt{(v.x-goal.x)^2 + (v.y-goal.y)^2}</tex>. | ||
| + | |||
| + | Также стоит обратить внимание на то как соотносятся <tex>f(v)</tex> и <tex>h(v)</tex>. Если они измеряются в разных величинах(Например, <tex>g(v)</tex> это расстояние в километрах, а <tex>h(v)</tex> {{---}} оценка времени пути в часах) А* может выдать некорректный результат. | ||
==Псевдокод== | ==Псевдокод== | ||
Версия 10:13, 31 декабря 2011
Алгоритм А*("A star", "А звёздочка") — алгоритм поиска, который находит во взвешенном графе маршрут наименьшей стоимости от начальной вершины до выбранной конечной.
Описание
В процессе работы алгоритма для вершин рассчитывается функция , где
- — наименьшая стоимость пути в из стартовой вершины,
- — эвристическое приближение стоимости пути от до конечной цели. должна быть эвристически допустимой, то есть не должна переоценивать рассояние до цели.
Чем меньше , тем раньше вершина будет открыта и исследована алгоритмом. Таким образом открытые алгоритмом вершины хранятся в очереди с приоритетом по значению . А* действует подобно алгоритму Дейкстры и просматривает среди всех маршрутов ведущих к цели сначала те, которые благодаря имеющейся информации(эвристическая функция) в данный момент являются наилучшими, причем алгоритм учитывает путь уже пройденный до текущей вершины.
Поведение алгоритма сильно зависит от того, какая эвристика используется. В свою очередь, выбор эвристики зависит от постановки задачи. Часто А* используется для моделирования перемещения по поверхности, покрытой координатной сеткой.Если мы можем перемещаться в четырех направлениях, в качестве эвристики стоит выбрать манхэттенское расстояние .
Расстояние Чебышева применяется когда к четырем направлениям добавляются диагонали.
Если передвижение не ограниченно сеткой, то можно использовать евклидово расстояние по прямой .
Также стоит обратить внимание на то как соотносятся и . Если они измеряются в разных величинах(Например, это расстояние в километрах, а — оценка времени пути в часах) А* может выдать некорректный результат.
Псевдокод
void A*(start,goal)
{
closed := {}; // Множество вершин расстояние до которых мы уже оценили
open.push(start);// Очередь с приоритетом
f[start] = g[start] + h[start];
parent[start] = start;
while (open.size() != 0)
{
x := open.pop();
if (x == goal)
return succsess(x);// Кратчайший путь найден
closed.push(x);
for (y : xy in E)
{
if (y in closed)
continue;
tmp := g[x] + d[x,y] // Стоимость пути до y через х
if (y not in open)
{
open.push(y);
tentative_is_better = true;
}
else
if (tmp < g[y]) // можно улучшить расстояние до y
tentative_is_better = true
else
tentative_is_better = false
if (tentative_is_better == true) // найден новый, более короткий путь до y
{
parent[y] = x;
g[y] = tmp;
f[y] = g[y] + h[y];
}
}
}
return failure; // Наша цель недостижима из start
}
Свойства
Корректность
Если всегда меньше либо равна истинной стоимости пути до цели, то А* гарантированно найдет кратчайший путь, причем чем меньше разница между эвристикой и истинной стоимостью, тем меньше вершин рассмотрит алгоритм.
Оптимальность
Любой другой алгоритм, использующий ту же эвристическую функцию , рассмотрит не меньше вершин, чем А*.