Эргодическая марковская цепь — различия между версиями
Whiplash (обсуждение | вклад) |
Whiplash (обсуждение | вклад) м |
||
| Строка 3: | Строка 3: | ||
:<tex>\lim\limits_{n \to \infty} p_{ij}^{(n)} = \pi_j, \quad \forall i=1,2, \ldots</tex>. | :<tex>\lim\limits_{n \to \infty} p_{ij}^{(n)} = \pi_j, \quad \forall i=1,2, \ldots</tex>. | ||
}} | }} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Основная теорема об эргодических распределениях== | ==Основная теорема об эргодических распределениях== | ||
Версия 01:48, 1 января 2012
| Определение: |
Марковская цепь называется эргодической, если существует дискретное распределение (называемое эргодическим) , такое что и
|
Содержание
Основная теорема об эргодических распределениях
| Теорема (Основная теорема об эргодических распределениях): |
Пусть - цепь Маркова с дискретным пространством состояний и матрицей переходных вероятностей . Тогда эта цепь является эргодической тогда и только тогда, когда она
Эргодическое распределение тогда является единственным решением системы:
|
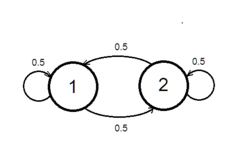
Пример
Рассмотрим эксперимент по бросанию честной монеты. Тогда соответствующая этому эксперименту марковская цепь будет иметь 2 состояния. Рассмотрим матрицу, следующего вида: .
Такая матрица является стохастической, а, значит, корректно определяет марковскую цепь. Такая цепь является эргодической, так как существует эргодическое распределение , такое что .
См. также
Примечания
- ↑ Свойство сообщаемости порождает на пространстве состояний отношение эквивалентности. Порождаемые классы эквивалентности называются неразложимыми классами.
Ссылки
Литература
Дж. Кемени, Дж. Снелл "Конечные цепи Маркова" - Издательство "Наука", 1970 г - 129 c.