Реализация булевой функции схемой из функциональных элементов — различия между версиями

Материал из Викиконспекты
Перейти к: навигация, поиск
(внесена т.н. теорема из статьи "Изменение размера оптимальной схемы при переходе к другому базису")
Строка 69: Строка 69:
  
 
[http://www.intuit.ru/department/calculate/lancalc/2/  Лекция "Схемы из функциональных элементов" в Интернет Университете Информационных Технологий]
 
[http://www.intuit.ru/department/calculate/lancalc/2/  Лекция "Схемы из функциональных элементов" в Интернет Университете Информационных Технологий]
 +
 +
[[Категория: Дискретная математика и алгоритмы]]
  
 
[[Категория: Схемы из функциональных элементов ]]
 
[[Категория: Схемы из функциональных элементов ]]

Версия 22:28, 16 января 2012

Логические элементы

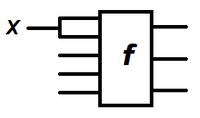
Функциональный элемент (англ. Combinational element) — устройство, предназначенное для обработки информации в цифровой форме. Функциональный элемент имеет входы и выходы. Сигналы на входах функционального элемента — аргументы функции, которую реализует функциональный элемент, сигналы на выходах — значение функции от аргументов.

Если входные и выходные сигналы — являются нулями и единицами, элемент называется логическим (англ. logic gate). При подаче на входы логического элемента любой комбинации двоичных сигналов, на выходах также возникает сигнал — значение булевой функции.

Отождествление переменных

Отождествление переменных осуществляется при помощи ветвления проводников.
Отождествление переменных

Подстановка

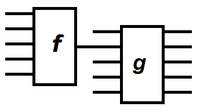
Чтобы осуществить подстановку одной функции в другую нужно выход логического элемента, который реализует первую функцию, направить на вход логического элемента, который реализует вторую функцию.

Подстановка

Изображение логических элементов на схемах

Тип элемента И ИЛИ НЕ Штрих Шеффера Стрелка Пирса
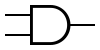
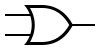
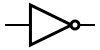
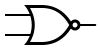
Традиционная форма AND logic element.png OR logic element.png NOT logic element.png NAND logic element.png NOR logic element.png
Прямоугольная форма AND logic relement.png

AND logic relement2.png

OR logic relement.png

OR logic relement2.png

NOT logic relement.png NAND logic relement.png

NAND logic relement2.png

NOR logic relement.png

NOR logic relement2.png

Схемная сложность

Определение:
Схемная сложность функции [math]f[/math] относительно базиса [math]B[/math] — это минимальное количество функциональных элементов из набора [math]B[/math], необходимое для реализации функции [math]f[/math] в базисе [math]B[/math]. Схемную сложность функции [math]f[/math] в базисе [math]B[/math] обозначают так: [math]size_B(f)[/math]


Теорема:
Для любых базисов [math]~B_1[/math], [math]~B_2[/math] и функции [math]~f[/math] верно неравенство [math]~size_{B_2}(f) \leq C_{(B_1,\;B_2)}size_{B_1}(f)[/math], где константа [math]~C[/math] зависит только от базисов [math]~B_1[/math] и [math]~B_2[/math].
Доказательство:
[math]\triangleright[/math]
Пусть базис [math]~B_2[/math] состоит из функций [math]~g_1, g_2, ..., g_n[/math]. Каждый функциональный элемент базиса [math]~B_2[/math] можно собрать с помощью элементов не более чем [math]~size_{B_1}(g_i)[/math] элементов из базиса [math]~B_1[/math]. Собрать [math]f[/math] в базисе [math]B_1[/math] можно следующим образом: заменить каждый элемент схемы [math]f[/math] в базисе [math]B_2[/math] на схему соответствующей функции в базисе [math]B_1[/math]. Такая сборка использует не более чем в [math]~C = \max_{i=1}^n size_{B_1}(g_i)[/math] раз больше функциональных элементов, чем соответствующая схема в [math]B_2[/math]. Параметр [math]~C[/math] зависит только от выбранных базисов.
[math]\triangleleft[/math]

Литература

Кормен, Т., Лейзерсон, Ч., Ривест, Р. Алгоритмы: построение и анализ = Introduction to Algorithms / Пер. с англ. под ред. А. Шеня. — М.: МЦНМО, 2000. — 960 с. — ISBN 5-900916-37-5

Ссылки

Статья Logic Gate на английской википедии

Лекция "Схемы из функциональных элементов" в Интернет Университете Информационных Технологий

Источник — «http://neerc.ifmo.ru/wiki/index.php?title=Реализация_булевой_функции_схемой_из_функциональных_элементов&oldid=16825»