Лемма о разрастании для КС-грамматик — различия между версиями
| Строка 12: | Строка 12: | ||
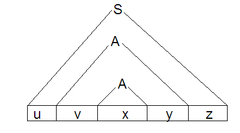
Найдем слова <tex> u,v,x,y,z </tex>. | Найдем слова <tex> u,v,x,y,z </tex>. | ||
| − | *Рассмотрим нетерминал <tex>A</tex>, содержащийся в поддереве выбранного нетерминала. Тогда <tex>x</tex> - строка терминалов которая | + | *Рассмотрим нетерминал <tex>A</tex>, содержащийся в поддереве выбранного нетерминала. Тогда <tex>x</tex> - строка терминалов которая выведена из рассмотренного нетерминала в данном дереве разбора. <tex>A \Rightarrow^{*} x</tex>. |
| − | *Рассмотрим выбранный нетерминал <tex>A</tex>. Пусть <tex>t</tex> - строка терминальных символов, которая | + | *Рассмотрим выбранный нетерминал <tex>A</tex>. Пусть <tex>t</tex> - строка терминальных символов, которая выведена из рассмотренного нетерминала в данном дереве разбора. Тогда <tex>A \Rightarrow^{*}\alpha A \beta \Rightarrow^{*} t</tex>, где <tex>\alpha,\beta</tex> - строки, состоящие из терминалов, которые могут содержать как терминалы, так и нетерминалы. При этом, как минимум одна из строк <tex>\alpha,\beta</tex> не пуста, так как грамматика языка записана в НФХ. Пусть <tex>v,y</tex> - строки, состоящие из терминалов, которые выведены из <tex>\alpha,\beta</tex> соответственно, в данном дереве разбора. Тогда <tex>t = vxy</tex>. Так как хотя бы одна из строк <tex>\alpha,\beta</tex> не пуста, то <tex>vy\neq \varepsilon</tex>. Получаем <tex>A \Rightarrow^{*} vAy \Rightarrow^{*} vxy</tex>. |
| − | * | + | *Рассмотрим стартовый нетерминал <tex>S</tex>. Из <tex>S</tex> выведена строка <tex>\omega</tex>. При этом <tex>S \Rightarrow^{*} \alpha A \beta \Rightarrow^{*} \omega </tex>, где <tex>A</tex> - выбранный ранее нетерминал. Из <tex>A</tex> в данном дереве разбора выведена строка <tex>vxy</tex>. Пусть <tex>u,z</tex> - строки, состоящие из терминалов, которые выведены из <tex>\alpha,\beta</tex> соответственно, в данном дереве разбора. Тогда <tex>S \Rightarrow^{*} uAz \Rightarrow^{*} uvAyz \Rightarrow^{*} \omega</tex>. |
| − | + | Таким образом, в рамках нашей грамматики мы можем построить цепочку вывода: <tex>S \Rightarrow^{*} uAz \Rightarrow^{*} uvAyz \Rightarrow^{*} uvvAyyz \Rightarrow^{*} uv^{k}Ay^{k}z \Rightarrow^{*} uv^{k}xy^{k}z</tex>. | |
| − | Таким образом, <tex>S \Rightarrow^{*} uAz \Rightarrow^{*} uvAyz \Rightarrow^{*} uvvAyyz \Rightarrow^{*} uv^{k}Ay^{k}z \Rightarrow^{*} uv^{k}xy^{k}z</tex>. | ||
}} | }} | ||
Версия 23:17, 23 января 2012
| Лемма (о разрастании КС-грамматик): |
Пусть — контекстно-свободный язык над алфавитом , тогда существует такое , что для любого слова длины не меньше найдутся слова , для которых верно: и . |
| Доказательство: |
|
Грамматика любого контекстно-свободного языка может быть записана в нормальной форме Хомского (НФХ). Пусть — количество нетерминалов в грамматике языка , записанной в НФХ.
Выберем . Построим дерево разбора произвольного слова длиной больше, чем . Высотой дерева разбора назовем максимальное число нетерминальных символов на пути от корня дерева к листу. Так как грамматика языка записана в НФХ, то у любого нетерминала в дереве могут быть, либо два потомка нетерминала, либо один потомок терминал. Поэтому высота дерева разбора слова не меньше . Количество нетерминалов в нем не меньше, чем , следовательно, найдется такой нетерминал , который встречается на этом пути дважды. Значит, в дереве разбора найдется нетерминал , в поддереве которого содержится нетерминал . Выберем нетерминал , у которого в поддереве содержится такой же нетерминал и длина пути до корня максимальна среди всех нетерминалов, содержащих в поддереве такой же нетерминал. Найдем слова .
|