Трапецоидная карта — различия между версиями
Shagal (обсуждение | вклад) |
Shagal (обсуждение | вклад) (→Алгоритм) |
||
| Строка 78: | Строка 78: | ||
==Алгоритм== | ==Алгоритм== | ||
| − | + | [[Файл:Trapezoidmapnotsuchbadcaseshagal.jpg|400px|thumb|right|простой случай]] | |
| − | + | Во время построения трапецоидной карты(в дальнейшем <tex> T</tex>) алгоритм так же строит структуру для поиска (в дальнейшем <tex> D</tex>). | |
| − | + | ||
| − | + | Так как трапецоидная карта - геометрическая структура, а основные операции ведутся именно с поисковой, упор на неё. | |
| − | + | ||
| − | + | Наш алгоритм добавляет отрезки по одному и после каждого добававления модидицирует <tex> T</tex> и <tex> D</tex>. | |
| − | + | ||
| − | + | ''Порядок добавления отрезков'' | |
| − | + | ||
| − | + | От порядка добавления зависит время запроса. Как? Время запрос пропорцианально глубине графа. | |
| − | + | ||
| − | + | Считается, что еслли добавлять отрезки рандомно, то время будет хорошим. Почему и какое время будет рассписано дальше. | |
| − | + | ||
| − | + | ''Алгоритм'' | |
| − | + | ||
| − | + | *Добавили отрезок. | |
| − | + | ||
| − | + | *Нашли все трапецоиды, которые пересек новый отрезок. | |
| − | + | ||
| − | + | *Удалили их. | |
| − | + | ||
| − | + | ||
| − | + | *Создали новый трапецоиды. | |
| − | + | [[Файл:Trpezoidmapbadcaseshagal.jpg|400px|thumb|right|сложный случай]] | |
| − | + | Рассмотрим подробнее последние две части | |
| + | Есть два случая. | ||
| + | *Простой - отрезок не пересекает ни одного трапецоида, то есть целеком внутри. | ||
| + | |||
| + | Тогда удаляем этот старый трапецоид и на его место ставим дерево из двух концов отрезка, отрезка и четырех образовавшихся трапецоидов. | ||
| + | |||
| + | Важно не забыть правильно определить соседей новых трапецоидов. | ||
| + | |||
| + | |||
| + | В случаи если какие-то трапецоиду выродятся в треугольники будет не четыре новых трапецоида , а 2 или 3. Слава богу это не самая большая проблема. | ||
| + | |||
| + | *Сложный - отрезок пересекает сразу несколько трапецоидов. | ||
| + | |||
| + | Итак наш отрезок пересекает трапецоиды <tex>\Delta_0, \Delta_1, \Delta_2 ... \Delta_k</tex>. | ||
| + | |||
| + | Сначала очередь добавляем вертикальные лучи из концов текущего отрезка. Это нужно, чтобы модифицировать <tex>\Delta_0 и \Delta_k</tex>. | ||
| + | |||
| + | Дальше мы модифицуруем вертикальные лучи, которые пересекают текущий отрезок. Этот процесс происходит достаточно быстро, так мы храним много информацию об этих лучах в | ||
| + | |||
| + | По хорошему то как этот происходит просто ужасно и видеть это не хочется, а все потому, что много что добавляется много новых узлов. | ||
| + | |||
| + | <tex>\Delta_0, \Delta_1, \Delta_2 ... \Delta_k</tex>. Теперь мы должны удалить соответствующие листья и на новые которые появились из-за изменения лучей. | ||
Версия 22:54, 15 февраля 2012
Трапецоидная карта - геометрическая структура позволяющая локализоваться на площади за .
Постановка задачи
Предположим, у нас есть наши координаты, и есть карта мира. Мы можем найти по карте наше местоположение и сказать в какой области мы находимся. Области задаются отрезками. Формальная постановка задачи Есть множество отрезков на плоскости. Есть запрос (точка q), на выход подается область заданная какими-то отрезками в которой находится q.
Структура данных
- Геометрическая
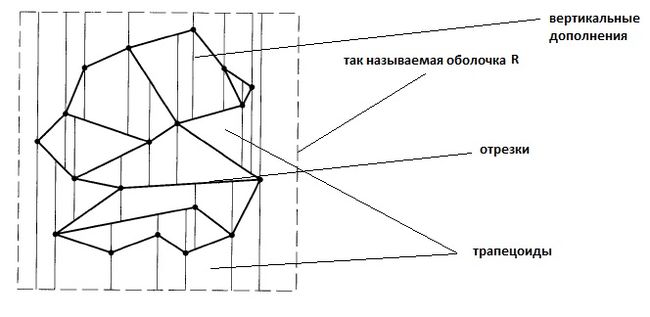
У нас есть множество отрезков ограничееных оболочкой R(это не выпуклая оболочка, а просто мнимая граница плоскости за которую не вылезают отрезки)
Мы договариваемся что никакие две точки не лежат на одной вертикале(в противном случаи все еще противнее)
Трапецоидная карта множества отрезков S - это эти отрезки + из кажой точки выпущены два луча, вверх и вниз до первого пересечения с другим отрезком или с оболочкой R.
| Лемма: |
Любой face трапецоидной карты ограничен одним или двумя вертикальными отрезками и обязательно двумя не вертикальными отрезками. |
Именно отсюда берется название стрктуры, так как любой face либо трапеция, либо треугольник.
Введем обозначения для навигации по карте.
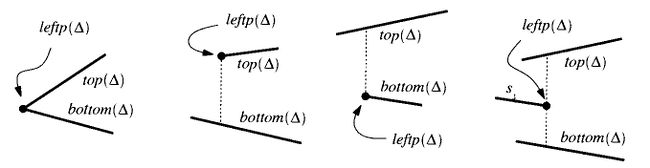
- левая граница(leftp) - точка определяющая левуюы сторону трапецоида или в случаи треугольника просто являющаяся левой вершиной.
- правая граница(rightp) - аналогично левой только справа.
- верхний отрезок(top) и нижний отрезок(bottom) - отрезки ограничивающие трапецоид сверху и снизу.
- трапецоиды называются смежными, если имеют общую вертикальную границу.
- пусть смежны и либо top() = top(), либо bottom() = bottom()
Тогда , называют либо большими левыми соседями, либо меньшими.
Хранить трапецоиды можно в чем угодно. Вместе с самим трапецоидом, стоит хранить leftp, rightp, top и bottom так же следует хранить соседей трапецоида.
- Поисковая структура
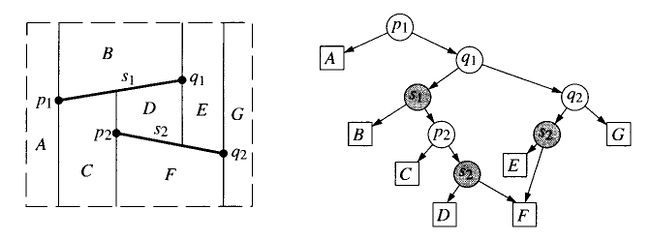
Поисковая структура(в дальнейшем ) предсталяет из себя ацикличный граф с одним корнем и каждому трапецоиду в структре соответствует один лист.
У каждого узла есль два ребенка и при этом узел может быть двух типов.
Первый тип узла - точка, соответствующая концу отрезка.
Второй тип узла - отрезок.
Во время запроса мы двигаемся по графу от его корня до момента, когда окажемся в листе, это и будет означать что точка находится внутри трапецоида.
Если мы находимся не в листе, то мы должны опрелетиться в каком из детей мы окажемся дальше.
Еcть два правила:
- Если текущий узел соответсвует вершине, то смотрим левее или провее мы находимся(проверка по x-координате).
- Если текущий узел соответствует отрезку, то смотрим выше или ниже мы находимся(проверка по y-координате).
- Плохие случаи:
Мы находимся на одной вертикале с вершиной
Мы находимся на отрезке
(Решение: молиться, или просто обрабатывать вручную.)
Алгоритм
Во время построения трапецоидной карты(в дальнейшем ) алгоритм так же строит структуру для поиска (в дальнейшем ).
Так как трапецоидная карта - геометрическая структура, а основные операции ведутся именно с поисковой, упор на неё.
Наш алгоритм добавляет отрезки по одному и после каждого добававления модидицирует и .
Порядок добавления отрезков
От порядка добавления зависит время запроса. Как? Время запрос пропорцианально глубине графа.
Считается, что еслли добавлять отрезки рандомно, то время будет хорошим. Почему и какое время будет рассписано дальше.
Алгоритм
- Добавили отрезок.
- Нашли все трапецоиды, которые пересек новый отрезок.
- Удалили их.
- Создали новый трапецоиды.
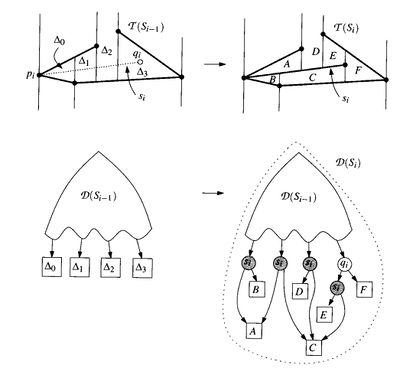
Рассмотрим подробнее последние две части Есть два случая.
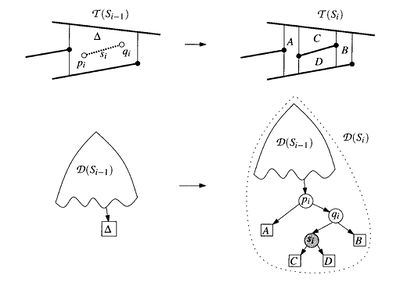
- Простой - отрезок не пересекает ни одного трапецоида, то есть целеком внутри.
Тогда удаляем этот старый трапецоид и на его место ставим дерево из двух концов отрезка, отрезка и четырех образовавшихся трапецоидов.
Важно не забыть правильно определить соседей новых трапецоидов.
В случаи если какие-то трапецоиду выродятся в треугольники будет не четыре новых трапецоида , а 2 или 3. Слава богу это не самая большая проблема.
- Сложный - отрезок пересекает сразу несколько трапецоидов.
Итак наш отрезок пересекает трапецоиды .
Сначала очередь добавляем вертикальные лучи из концов текущего отрезка. Это нужно, чтобы модифицировать .
Дальше мы модифицуруем вертикальные лучи, которые пересекают текущий отрезок. Этот процесс происходит достаточно быстро, так мы храним много информацию об этих лучах в
По хорошему то как этот происходит просто ужасно и видеть это не хочется, а все потому, что много что добавляется много новых узлов.
. Теперь мы должны удалить соответствующие листья и на новые которые появились из-за изменения лучей.