Граф компонент рёберной двусвязности — различия между версиями
м |
|||
| Строка 4: | Строка 4: | ||
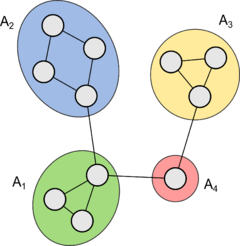
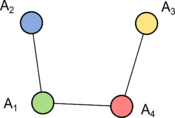
Построим граф <tex>T</tex>, в котором вершинами будут <tex>A_1\ldots A_n</tex>, а ребрами {{---}} <tex>a_1\ldots a_m</tex>, соединяющими соответствующие вершины из соответствующих компонент реберной двусвязности. Полученный граф <tex>T</tex> называют '''графом компонент [[Отношение реберной двусвязности|реберной двусвязности]]''' графа <tex>G</tex>. | Построим граф <tex>T</tex>, в котором вершинами будут <tex>A_1\ldots A_n</tex>, а ребрами {{---}} <tex>a_1\ldots a_m</tex>, соединяющими соответствующие вершины из соответствующих компонент реберной двусвязности. Полученный граф <tex>T</tex> называют '''графом компонент [[Отношение реберной двусвязности|реберной двусвязности]]''' графа <tex>G</tex>. | ||
}} | }} | ||
| − | <div class="tleft" style="clear:none">[[Файл:Double_edge_1.png|thumb| | + | <div class="tleft" style="clear:none">[[Файл:Double_edge_1.png|thumb|240px|Граф <tex>G</tex>]]</div> |
| − | <div class="tleft" style="clear:none">[[Файл:Double_edge_2.png|thumb| | + | <div class="tleft" style="clear:none">[[Файл:Double_edge_2.png|thumb|175px|Граф <tex>T</tex>]]</div> |
{{Лемма | {{Лемма | ||
|statement= | |statement= | ||
Версия 19:42, 23 апреля 2012
| Определение: |
| Пусть граф связен. Обозначим — компоненты реберной двусвязности, а — мосты . Построим граф , в котором вершинами будут , а ребрами — , соединяющими соответствующие вершины из соответствующих компонент реберной двусвязности. Полученный граф называют графом компонент реберной двусвязности графа . |
| Лемма: |
В определении, приведенном выше, — дерево. |
| Доказательство: |
|
а) — связно. (Следует из определения) б) В нет циклов. Пусть какие-то две смежные вершины и принадлежат какому-то циклу. Тогда ребро принадлежит этому же циклу. Следовательно, существуют два реберно-непересекающихся пути между вершинами и , т.е. — не является мостом. Но — мост по условию. Получили противоречие. — дерево. |