Суффиксный бор

Суффиксный бор для строки [math]abbc[/math]

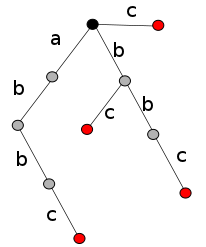
Суффиксный бор (англ. suffix trie) — бор, содержащий все суффиксы данной строки.

По определению, в суффиксном боре для строки [math]s[/math] (где [math]\lvert s\rvert=n[/math]) содержатся все строки [math]s[1..n], ..., s[n..n][/math]. Сделаем следующее наблюдение: если в суффиксном боре находится строка [math]s[i..n][/math], то все ее префиксы [math]s[i..j], i \le j \le n[/math] уже содержатся в нашем боре. Значит, суффиксный бор можно использовать для поиска всех подстрок строки [math]s[/math] (чтобы бор формально содержал все подстроки [math]s[/math], нужно пометить все его вершины терминальными, при этом корень будет соответствовать пустой строке [math]\varepsilon[/math]).

Свойства

Суффиксный бор для строки [math]s[/math]:

• Можно использовать для поиска образца [math]p[/math] в строке [math]s[/math] за время [math]O(\lvert p\rvert)[/math].
• Можно построить за время [math]O(n^2)[/math], последовательно добавив все суффиксы [math]s[/math].
• Имеет порядка [math]n^2[/math] вершин.

Реализация

int [length^2][alphabet] trie 
number [math] \leftarrow [/math]1 
Add(i, j)
  current [math]\leftarrow[/math] 0 
  for (char c [math]\in[/math] s[i, j])
    if (trie[current][c] [math]\neq  [/math]  -1)
      trie[current][c] [math] \leftarrow[/math] number 
      number++; 
    current [math]\leftarrow[/math] trie[current][c]
Build(String  s)
  добавляем все суффиксы.

Хранение в памяти

Пусть [math]s \in \Sigma^*[/math], [math]\lvert s\rvert = n[/math]. Из третьего свойства следует, что для хранения суффиксного бора в худшем случае потребуется [math]O(n^2 |\Sigma|)[/math] памяти. Например, если строка состоит из всех символов алфавита. Количество разветвлений будет равно количеству суффиксов, так как каждый лист соответствует единственному суффиксу. Количество суффиксов [math]n[/math]. Тогда количество вершин, в которых больше одного перехода будет [math]O(n)[/math]. Поэтому, если вместо массива переходов для вершин хранить map<char, integer>, то можно получить оценку [math]O(n^2 + n|\Sigma|)[/math]. Улучшением суффиксного бора, расходующим всего [math]O( n|\Sigma|)[/math] памяти, является сжатое суффиксное дерево.