Meet-in-the-middle

Определение:

Meet-in-the-middle (Встреча в середине) — это метод решения уравнения вида [math] f({x}) = g({y}) [/math], где [math] x \in {X} [/math] и [math] y \in {Y} [/math], который работает за время [math] {O((X + Y)\log{X}})[/math].

Meet-in-the-middle разбивает задачу пополам и решает всю задачу через частичный расчет половинок. Он работает следующим образом : переберем все возможные значения [math] {x} [/math] и запишем пару значений [math] ({x},{f({x})}) [/math] в массив, который мы отсортируем по второму элементу (значению функции). Затем будем перебирать всевозможные значения [math] {y} [/math], для каждого из них будем вычислять [math] f({y}) [/math], которое мы будем искать в нашем отсортированном массиве. Таким образом, время работы нашего алгоритма составляет [math] {O(X\log{X})} [/math] на сортировку, и [math] {O(Y\log{Y})} [/math] на двоичный поиск, что дает в сумме [math]{O((X + Y)\log{X}})[/math]

Задача о нахождение четырех чисел с суммой равной нулю

Дан массив целых чисел [math]{A}[/math]. Требуется найти любые 4 числа, сумма которых равна 0 (одинаковые элементы могут быть использованы несколько раз).

Например : [math] {A} = ({2,3,1,0,-4,-1}) [/math]. Решением данной задачи является, например, четверка чисел [math] 3 + 1 + 0 - 4 = 0[/math] или [math] 0 + 0 + 0 + 0 = 0[/math].

Наивный алгоритм заключается в переборе всевозможных комбинаций чисел. Это решение работает за [math] {O(N^4)}[/math]. Теперь, с помощью Meet-in-the-middle мы можем сократить время работы до [math] {O((N + N)\log{N}}) = {O(N^2\log{N}}) [/math].

Для этого заметим, что сумму [math] a + b + c + d = 0 [/math] можно записать как [math] a + b = -(c + d)[/math]. Мы будем хранить все [math] {N^2} [/math] пар сумм [math] a + b [/math] в массиве [math] sum [/math], который мы отсортируем. Далее перебираем все [math] {N^2} [/math] пар сумм [math] c + d [/math] и проверяем бинарным поиском, есть ли сумма [math] -(c + d) [/math] в массиве [math] sum [/math].

Псевдокод

 // sum - массив сумм a + b, cnt - счетчик массива sum
 for a = 0 to N - 1
   for b = 0 to N - 1
     sum[cnt].s = A[a] + A[b];
     sum[cnt].a = a;
     sum[cnt++].b = b;
 sort(sum);
 
 for c = 0 to N - 1
   for d = 0 to N - 1
     if (сумма -(A[c] + A[d]) есть в массиве sum)
       ind = индекс суммы -(A[c] + A[d]) в массиве sum;
       print(sum[ind].a, sum[ind].b, A[c], A[d]);
       return;
 print("No solution");

Итоговое время работы [math] {O(N^2\log{N}}) [/math].

Задача о рюкзаке

Классической задачей является задача о наиболее эффективной упаковке рюкзака. Каждый предмет характеризуется весом ([math] {w_{i} \lt = 10^{9}} [/math] ) и ценностью ([math]{cost_{i} \lt = 10^{9}} [/math]). В рюкзак, ограниченный по весу, необходимо набрать вещей с максимальной суммарной стоимостью. Для ее решения изначальное множество вещей N разбивается на два равных(или примерно равных) подмножества, для которых за приемлемое время, можно перебрать все варианты и подсчитать суммарный вес и стоимость, а затем для каждого из них найти группу вещей из первого подмножества с максимальной стоимостью, укладывающуюся в ограничение по весу рюкзака. Сложность алгоритма [math]O({2^{N/2}}\times{N})[/math]. Память [math] O({2^{N/2}})[/math]

Реализация

Разделим наше множество на две части. Подсчитаем все подмножества из первой части и будем хранить их в массиве [math] first [/math]. Отсортируем массив [math] first [/math] по весу. Далее пройдемся по этому массиву и оставим только те подмножества, для которых не существует другого подмножества с меньшим весом и большей стоимостью. Очевидно, что подмножества, для которых существует другое, более легкое и одновременно более ценное подмножество, можно удалять. Таким образом в массиве [math] first [/math] мы имеем подмножества, отсортированные не только по весу, но и по стоимости. Тогда начнем перебирать все возможные комбинации вещей из второй половины и находить бинарным поиском удовлетворяющие нас подмножества из первой половине, хранящиеся в массиве [math] first [/math].

Реализуем данный алгоритм:

 // N - количество всех вещей, w[] - массив весов всех вещей, cost[] - массив стоимостей всех вещей, R - ограничение по весу рюкзака.
 sn = N / 2, fn = N - sn;
 for mask = 0 to 2 ** sn - 1
   for j = 0 to sn
     if j-ый бит mask = 1
       first[i].w += w[j];
       first[i].c += cost[j];
 sort(first);
 for i = 0 to 2 ** sn - 1
   if (существует такое подмножество с индексом j, что first[j].w <= first[i].w && first[j].c >= first[i].c)
     удалим множество с индексом i из массива first
 
 for mask = 0 to 2 ** fn - 1
   for j = 0 to fn
     if j-ый бит mask = 1
       curw += w[j + sn];
       curcost += cost[j + sn];
   
   В массиве first бинарным поиском находим подмножество, с максимальным весом, который не превышает R - curw
   if (first[index].w <= R - curw && first[index].c + curcost > ans)
     ans = first[index].c + curcost
 print ans

Итоговое время работы [math] {O({2^{N/2}}\times({N}+\log{2^{N/2}}))} = O({2^{N/2}}\times{N}) [/math].

Задача о нахождении кратчайшего расстояния между двумя вершинами в графе

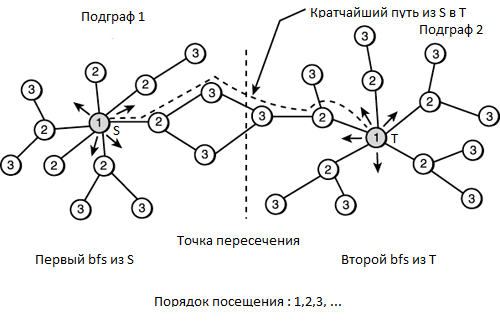
Нахождение кратчайшего расстояния между двумя вершинами

Еще одна задача, решаемая Meet-in-the-middle — это нахождение кратчайшего расстояния между двумя вершинами, зная начальное состояние, конечное состояние и то, что длина оптимального пути не превышает N. Стандартным подходом для решения данной задачи, является применение алгоритма обхода в ширину. Пусть из каждого состояния у нас есть K переходов, тогда бы мы сгенерировали [math] {K^{n}} [/math] состояний. Асимптотика данного решения составила бы [math] {O({K^{n}})} [/math]. Meet-in-the-middle помогает снизить асимптотику до [math] {O({K^{n/2}})} [/math].

Алгоритм решения

1. Сгенерируем bfs-ом все состояния, доступные из начала и конца за [math] {n/2} [/math] или меньше ходов.

2. Найдем состояний, которые достижимы из начала и из конца.

3. Найдем среди них наилучшее по сумме длин путей.

Таким образом, bfs-ом из двух концов, мы сгенерируем максимум [math] {O({K^{n/2}})} [/math] состояний.

См. также

• Обход в ширину

Cсылки

• Meet-in-the-middle
• Лекции по информатике(36 страница)