Регулярная аппроксимация КС-языков — различия между версиями
Danek g30 (обсуждение | вклад) (→Идея алгоритма) |
Danek g30 (обсуждение | вклад) (→Апроксимации самоприменимой грамматики) |
||
| Строка 87: | Строка 87: | ||
makeFA (<tex> q_0, \beta, q_1 </tex>) | makeFA (<tex> q_0, \beta, q_1 </tex>) | ||
| − | == | + | == Аппроксимации самоприменимой грамматики == |
| − | В данном разделе покажем методы апроксимации самоприменимой | + | В данном разделе покажем методы апроксимации самоприменимой свободно-контекстной грамматики <tex> G = \langle N, \Sigma, P, S \rangle</tex> к регулярной грамматике. Для удобства будем считать, что грамматика представлена в [[Нормальная форма Хомского|НФХ]]. |
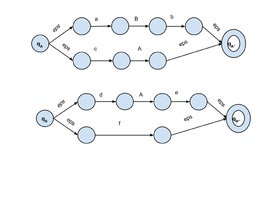
[[Файл:RTN_Automat.png|280px|thumb|right|Автоматы <tex>T_A,T_B</tex> для грамматики | [[Файл:RTN_Automat.png|280px|thumb|right|Автоматы <tex>T_A,T_B</tex> для грамматики | ||
<tex>A \rightarrow aBb \\ A \rightarrow cA \\ B \rightarrow dAe \\ B \rightarrow f </tex>]] | <tex>A \rightarrow aBb \\ A \rightarrow cA \\ B \rightarrow dAe \\ B \rightarrow f </tex>]] | ||
| − | === RTN | + | === RTN аппроксимация === |
Построим, по данной грамматике аппроксимирующий ее конечный автомат. | Построим, по данной грамматике аппроксимирующий ее конечный автомат. | ||
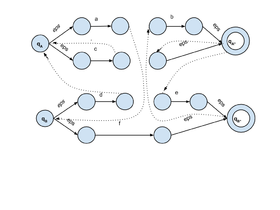
[[Файл:RTN_Automat1.png|280px|thumb|left|Конечный автомат для грамматики | [[Файл:RTN_Automat1.png|280px|thumb|left|Конечный автомат для грамматики | ||
| Строка 109: | Строка 109: | ||
| − | ===MT | + | ===MT аппроксимация === |
Построим, по данной самоприменимой кс грамматике <tex> G </tex>, регулярную грамматику <tex> G^*</tex>. | Построим, по данной самоприменимой кс грамматике <tex> G </tex>, регулярную грамматику <tex> G^*</tex>. | ||
#Для каждого нетерминала <tex> A \in N </tex> из <tex>G</tex>, добавим нетерминалы <tex>A</tex> и <tex> A^*</tex> в <tex> G^* </tex>. | #Для каждого нетерминала <tex> A \in N </tex> из <tex>G</tex>, добавим нетерминалы <tex>A</tex> и <tex> A^*</tex> в <tex> G^* </tex>. | ||
| Строка 122: | Строка 122: | ||
\\ B^* \rightarrow \alpha A^* | \varepsilon | \\ B^* \rightarrow \alpha A^* | \varepsilon | ||
\end{matrix}\right.</tex> | \end{matrix}\right.</tex> | ||
| + | |||
== Источники == | == Источники == | ||
* [http://books.google.ru/books?id=tFvtwGYNe7kC&pg=PA21&lpg=PA21&dq=prove+that+grammars+that+are+not+self-embedding+generate+regular+languages.&source=bl&ots=3gFnA7ig-l&sig=Ub9f_BJKv_jdiO7mWRvkYJVamDE&hl=ru&sa=X&ei=qQfcUoy9Nubb4QSI4YGQDg&redir_esc=y#v=onepage&q=prove%20that%20grammars%20that%20are%20not%20self-embedding%20generate%20regular%20languages.&f=false Формальное доказательство, что кс не самоприменимая грамматика генерирует регулярный язык] | * [http://books.google.ru/books?id=tFvtwGYNe7kC&pg=PA21&lpg=PA21&dq=prove+that+grammars+that+are+not+self-embedding+generate+regular+languages.&source=bl&ots=3gFnA7ig-l&sig=Ub9f_BJKv_jdiO7mWRvkYJVamDE&hl=ru&sa=X&ei=qQfcUoy9Nubb4QSI4YGQDg&redir_esc=y#v=onepage&q=prove%20that%20grammars%20that%20are%20not%20self-embedding%20generate%20regular%20languages.&f=false Формальное доказательство, что кс не самоприменимая грамматика генерирует регулярный язык] | ||
Версия 20:24, 19 января 2014
Содержание
Определения
| Определение: |
| Контекстно-свободная грамматика называется самоприменимой, если , . |
| Определение: |
| Нетерминал в грамматике называется рекурсивным, если . |
| Определение: |
| Нетерминалы в грамматике называются взаимно рекурсивными, если . |
Алгоритм преобразования грамматики в конечный автомат
| Лемма: |
Не самоприменимая контекстно-свободная грамматика генерирует регулярный язык. |
| Доказательство: |
| В качестве конструктивного доказательства, мы приведем алгоритм построения конечного автомата по грамматике. В источниках есть ссылка на формальное доказательство. |
Идея алгоритма
Пусть, множество рекурсивных терминалов из . Пусть, разбиение на дизъюнктных множеств взаимно рекурсивных терминалов, . Ввведем функцию :
function IsLeftType() return function IsRightType() return
function recursive (): if !IsLeftType() && IsRihtType() return left; if IsLeftType() && !IsRihtType() return right; if (IsLeftType() && IsRihtType() return self; if !IsLeftType() && !IsRihtType() return cyclic;
Заметим, что , т.к грамматика не самоприменима.
В основе алгоритма будет рекурсивный обход грамматики во все стороны. Спускаемся по грамматике до тех пор не приходим в нетерминал или символ алфавита:
- символ алфавит или — добавляем новое правило в автомат
- нерекурсивный нетерминал — запускаемся от всех правых частей правил, который терминал порождает
- рекурсивный нетерминал — в зависимости от типа рекурсивного нетерминала, продолжаем рекурсию (будет ясно из пседокода)
Псевдокод
— множество состояний ДКА. — множество переходов ДКА. — множество допускающих состояний.
function createFA(G) // s = createState f = createState return makeFA (s,S,f) function makeFA (q0,a,q1) if a == || a // пришли в лист дерева разбора return if a == where q = createState makeFA () makeFA () return if exist where foreach b in = createState if recursive() == left foreach C in where makeFA () foreach C,D in where makeFA () else // рекурсивный нетерминал rihgt или self foreach C in where makeFA () foreach C,D in where makeFA () return foreach p in where p == makeFA ()
Аппроксимации самоприменимой грамматики
В данном разделе покажем методы апроксимации самоприменимой свободно-контекстной грамматики к регулярной грамматике. Для удобства будем считать, что грамматика представлена в НФХ.
RTN аппроксимация
Построим, по данной грамматике аппроксимирующий ее конечный автомат.
- Для каждого нетерминала в грамматике, создадим новый конечный автомат , добавим два состояния в : .
- Для каждого правила грамматике , введм новые состояния в автомат этого нетерминала , а также добавим новые правила перехода в : .
- Таким образом мы построили множество конечных автоматов = для каждого нетерминала . Теперь объединим все в один автомат. Объединим все состоянии автоматов из в множество . Скопируем все переходы каждого автомата из в . Далее для каждого перехода вида , вместо него добавим два новых перехода: .
MT аппроксимация
Построим, по данной самоприменимой кс грамматике , регулярную грамматику .
- Для каждого нетерминала из , добавим нетерминалы и в .
- Для каждого правила , где . Добавим в нетерминалы и следуюшие правила: .
(Если , тогда добавим правило ).
В итоге — правоконтекстная грамматика, эквивалентная конечному автомату, который задает регулярный язык.
Пример