Троичный поиск

Троичный поиск (ternary search, тернарный поиск) — метод поиска минимума или максимума функции на отрезке.

Алгоритм

Пример. $f(a) \lt f(b) \Rightarrow x_{min} \in [l, b]$

Рассмотрим этот алгоритм на примере поиска минимума (поиск максимума аналогичен).

Пусть функция $f(x)$ на отрезке $[l, r]$ имеет минимум, и мы хотим найти точку $x_{min}$, в которой он достигается.

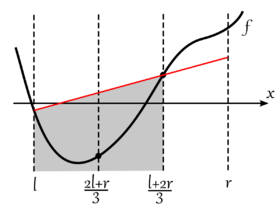
Посчитаем значения функции в точках $a = l +$ $\frac{(r-l)}{3}$ и $b = l +$ $\frac{2(r-l)}{3}$.

Так как в точке $x_{min}$ минимум, то на отрезке $[l, x_{min}]$ функция убывает, а на $[x_{min}, r]$ — возрастает, то есть

$\forall x', x'' \in [l, r]: \\ l \lt x' \lt x'' \lt x_{min} \Rightarrow f(l) \gt f(x') \gt f(x'') \gt f(x_{min}) \\ x_{min} \lt x' \lt x'' \lt r \Rightarrow f(x_{min}) \lt f(x') \lt f(x'') \lt f(r)$.

Значит если $f(a) \lt f(b)$, то $x_{min} \in [l, b]$, аналогично из $f(a) \gt f(b)$ следует $x_{min} \in [a, r]$.

Тогда нам нужно изменить границы поиска и искать дальше, пока не будет достигнута необходимая точность, то есть $r-l \lt \varepsilon$.

Псевдокод

Рекурсивный вариант:

ternarySearchMin(f, left, right, eps) 
    if (right - left < eps)
        return (left + right) / 2
    a = (left * 2 + right) / 3
    b = (left + right * 2) / 3
    if (f(a) < f(b))
        return ternarySearchMin(f, left, b, eps)
    else
        return ternarySearchMin(f, a, right, eps)

Итеративный вариант:

ternarySearchMin(f, left, right, eps) 
    while (right - left > eps) 
        a = (left * 2 + right) / 3
        b = (left + right * 2) / 3
        if (f(a) < f(b))
            right = b
        else
            left = a
    return (left + right) / 2

Время работы

Так как на каждой итерации мы считаем два значения функции и уменьшаем область поиска в полтора раза, пока $r - l \gt \varepsilon$, то время работы алгоритма составит $2 \log_{\frac32} \left(\dfrac{r - l}{\varepsilon}\right)$

См. также

• Поиск с помощью золотого сечения — оптимизация троичного поиска.
• Троичный поиск — Википедия
• Ternary search — Wikipedia

Литература

• Дональд Кнут — Искусство программирования. Том 3. Сортировка и поиск. / Knuth D.E. — The Art of Computer Programming. Vol. 3. Sorting and Searching.